广西壮族自治区南宁市西乡塘区2022-2023学年八年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 下列各式属于二次根式的是( )A、1 B、 C、 D、2. 下列长度的三条线段能组成直角三角形的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、5,6,73. 如图,在中, , 则( )
 A、30° B、50° C、60° D、120°4. 一组数据2,4,3,2,5的众数是( )A、5 B、3.5 C、3 D、25. 已知正比例函数 , 当时,则y的值为( )A、 B、 C、3 D、66. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )
A、30° B、50° C、60° D、120°4. 一组数据2,4,3,2,5的众数是( )A、5 B、3.5 C、3 D、25. 已知正比例函数 , 当时,则y的值为( )A、 B、 C、3 D、66. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )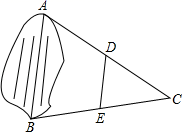 A、15m B、20m C、30m D、60m7. 计算 的结果是( )A、2 B、 C、 D、8. 在“双减”政策下,某学校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小颖的平时、期末成绩分别为80分,90分,则小颖本学期的学业成绩为( )A、92分 B、90分 C、86分 D、85分9. 直线的图象大致是( )A、
A、15m B、20m C、30m D、60m7. 计算 的结果是( )A、2 B、 C、 D、8. 在“双减”政策下,某学校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小颖的平时、期末成绩分别为80分,90分,则小颖本学期的学业成绩为( )A、92分 B、90分 C、86分 D、85分9. 直线的图象大致是( )A、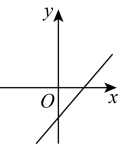 B、
B、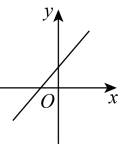 C、
C、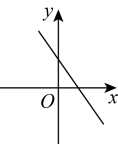 D、
D、 10. 如图,已知某菱形花坛的边长是 , , 则花坛对角线的长是( )
10. 如图,已知某菱形花坛的边长是 , , 则花坛对角线的长是( ) A、 B、 C、 D、11. 如图,图形是由两个直角三角形和三个正方形组成,若正方形A、B的面积分别为8、20,大直角三角形一边长为6,则斜边长m为( )
A、 B、 C、 D、11. 如图,图形是由两个直角三角形和三个正方形组成,若正方形A、B的面积分别为8、20,大直角三角形一边长为6,则斜边长m为( ) A、8 B、9 C、10 D、12. 一个有进水管与出水管的容器,从某时刻开始的内只进水不出水,在随后的内既进水又出水,之后只出水不进水,每分的进水量和出水量是两个常数,容器内的水量y(单位:)与时间x(单位:)之间的关系如图.则下列说法正确的是( )
A、8 B、9 C、10 D、12. 一个有进水管与出水管的容器,从某时刻开始的内只进水不出水,在随后的内既进水又出水,之后只出水不进水,每分的进水量和出水量是两个常数,容器内的水量y(单位:)与时间x(单位:)之间的关系如图.则下列说法正确的是( ) A、进水管每分钟的进水量为 B、当时, C、出水管每分钟的出水量为 D、水量为的时间为或
A、进水管每分钟的进水量为 B、当时, C、出水管每分钟的出水量为 D、水量为的时间为或二、填空题
-
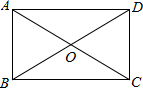
13. 式子有意义,则x的取值范围是 .14. 如图,在矩形中,对角线和交于点O , 若 , 则 .
 15. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是: , , 则射击成绩较稳定的是.(填“甲”或“乙”)16. 如图,直线: 与直线:相交于点 , 则关于x , y的方程组的解为 .
15. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是: , , 则射击成绩较稳定的是.(填“甲”或“乙”)16. 如图,直线: 与直线:相交于点 , 则关于x , y的方程组的解为 .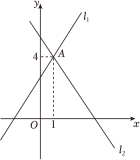 17. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.
17. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.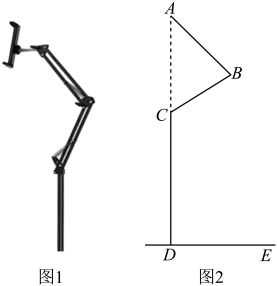 18. 平面直角坐标系中,O为坐标原点,直线与x轴、y轴分别交于两点,点C,点D坐标分别为 , 则的最小值为.
18. 平面直角坐标系中,O为坐标原点,直线与x轴、y轴分别交于两点,点C,点D坐标分别为 , 则的最小值为.
三、解答题
-
19. 计算: .20. 先化简,再求值: , 其中 .21. 水是生命之源,节约用水是每个公民应尽的义务.水龙头关闭不严会造成滴水,为了调查水量与漏水时间的关系,某同学在滴水的水龙头下放置了一个能显示水量的容器,每记录一次容器中的水量如下表:
时间
0
5
10
15
20
…
水量
0
25
50
75
100
…
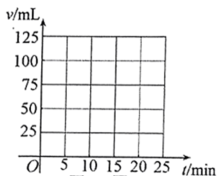 (1)、请根据上表中的信息,在图中描出以上述实验所得数据为坐标的各点;(2)、根据(1)中各点的分布规律,求出v关于t的函数解析式;(3)、请估算这种漏水状态下一天的漏水量.22. 如图,在中,点E在上,点F在上,且 .
(1)、请根据上表中的信息,在图中描出以上述实验所得数据为坐标的各点;(2)、根据(1)中各点的分布规律,求出v关于t的函数解析式;(3)、请估算这种漏水状态下一天的漏水量.22. 如图,在中,点E在上,点F在上,且 .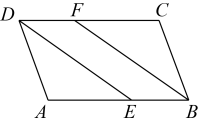 (1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.23. 在2023年体育中考中,扬帆中学初三学子再创佳绩.为做好总结,体育组老师随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):
(1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.23. 在2023年体育中考中,扬帆中学初三学子再创佳绩.为做好总结,体育组老师随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):扬帆中学初三学生体育中考成绩情况调查报告
调查主题
扬帆中学初三学生体育中考成绩
【设计调查方式】
随机抽取甲、乙两班各10名同学的体育中考成绩
【收集、整理、描述数据】
甲班抽取的10名同学的成绩:60,60,59,57,60,58,60,58,60,56.
乙班抽取的10名同学成绩的条形统计图:
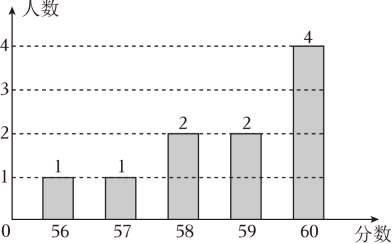
班级
平均分
众数
中位数
甲
60
m
乙
n
60
59
调查结论
…
请根据以上调查报告,解答下列问题;
(1)、填空:上述表格中, , ;(2)、根据以上数据,你认为甲、乙两班中哪个班的体育中考成绩更好?请说明理由(一条即可);(3)、该校初三有1200人参加体育中考,请估计满分的同学共有多少人?24. 螺蛳粉入选国家级非物质文化遗产名录,为满足广大消费者需求,某超市购进A、B两种品牌螺蛳粉,已知A品牌螺蛳粉比B品牌螺蛳粉每袋进价少2元,用3500元购进A品牌螺蛳粉与用4500元购进B品牌螺蛳粉的数量相同.(1)、A , B两种品牌螺蛳粉每袋的进价分别是多少元?(2)、本次购进A、B品牌螺蛳粉共900袋,每袋均按12元出售,且购进A品牌螺蛳粉的数量不超过B品牌螺蛳粉数量的2倍,若该批螺蛳粉全部售完,则该超市应购进A、B两种品牌螺蛳粉各多少袋才能获得最大利润?最大利润是多少元?25.(1)、【课本再现】如图,正方形的对角线相交于点 , 点又是正方形的一个顶点,边与边相交于点E , 边与边相交于点F , 在实验与探究中,小新发现通过证明 , 可得 . 请帮助小新完成证明过程;
(2)、【拓展推理】在(1)的条件下,连接 , 猜想之间的数量关系,并进行证明;
(3)、【迁移延伸】如图,矩形的对角线相交于点O , 点O又是矩形的一个顶点,边与边相交于点E , 边与边相交于点F , 连接 , 请判断(2)中的结论是否仍成立?若成立,请给出证明;若不成立,请说明理由.
 26. 如图,将矩形置于平面直角坐标系中,其中边在x轴上且A的坐标是 , . 过点A的直线l交y轴于点 , 将直线l沿y轴的正方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形的边截得的线段长度为m , 平移时间为t秒,m与t的函数图象如图所示.
26. 如图,将矩形置于平面直角坐标系中,其中边在x轴上且A的坐标是 , . 过点A的直线l交y轴于点 , 将直线l沿y轴的正方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形的边截得的线段长度为m , 平移时间为t秒,m与t的函数图象如图所示.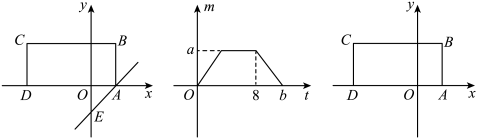 (1)、求直线l的函数解析式;(2)、直接写出矩形的面积,及图中a和b的值;(3)、在直线l的平移过程中,是否存在某个时刻使得直线l把矩形的面积分为的两部分,若成立,求出t的值;若不成立,请说明理由.
(1)、求直线l的函数解析式;(2)、直接写出矩形的面积,及图中a和b的值;(3)、在直线l的平移过程中,是否存在某个时刻使得直线l把矩形的面积分为的两部分,若成立,求出t的值;若不成立,请说明理由.