广西壮族自治区南宁市良庆区2022-2023学年七年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 下列各数为负数的是( )A、 B、 C、0 D、2. 2023年9月23日至10月8日第十九届亚运动会将在中国杭州举办,其中吉祥物“莲莲”深受大家喜爱,在下列的四个图中能由如图所示的图形平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )A、北纬 B、距气象台海里 C、北纬 , 东经 D、北海市附近4. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、5. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( )
3. 某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )A、北纬 B、距气象台海里 C、北纬 , 东经 D、北海市附近4. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、5. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( ) A、 B、 C、 D、6. “学习强国”平台,立足全体党员,面向全社会,某市有名党员注册学习,为了解党员学习积分情况,随机抽取了名党员学习积分进行调查,下列说法错误的是( )A、总体是该市名党员的“学习强国”积分 B、个体是每一名群众 C、样本是抽取的名党员的“学习强国”积分 D、样本容量是7. 如图,数轴上表示1,的对应点分别为A , B , 且 , 则点C所表示的数是( )
A、 B、 C、 D、6. “学习强国”平台,立足全体党员,面向全社会,某市有名党员注册学习,为了解党员学习积分情况,随机抽取了名党员学习积分进行调查,下列说法错误的是( )A、总体是该市名党员的“学习强国”积分 B、个体是每一名群众 C、样本是抽取的名党员的“学习强国”积分 D、样本容量是7. 如图,数轴上表示1,的对应点分别为A , B , 且 , 则点C所表示的数是( ) A、 B、 C、 D、8. 下列说法不正确的是( )A、为了解中央电视台《开学第1课》的收视率,采用抽样调查 B、为调查某单位职工学历情况占整体的百分比,采用扇形统计图 C、为调查神舟十四号飞船的零部件的质量,采用抽样调查 D、为调查某校初一班级学生的校服尺码,采用全面调查9. 小明和爸爸、妈妈三人玩跷跷板.爸爸的体重为75千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地,那么小明的体重应小于( )
A、 B、 C、 D、8. 下列说法不正确的是( )A、为了解中央电视台《开学第1课》的收视率,采用抽样调查 B、为调查某单位职工学历情况占整体的百分比,采用扇形统计图 C、为调查神舟十四号飞船的零部件的质量,采用抽样调查 D、为调查某校初一班级学生的校服尺码,采用全面调查9. 小明和爸爸、妈妈三人玩跷跷板.爸爸的体重为75千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地,那么小明的体重应小于( ) A、49千克 B、50千克 C、24千克 D、25千克10. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车备几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、11. 图是某品牌共享单车放在水平地面的实物图,图是其示意图,其中、都与地面平行, , , 若 , 则( )
A、49千克 B、50千克 C、24千克 D、25千克10. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车备几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、11. 图是某品牌共享单车放在水平地面的实物图,图是其示意图,其中、都与地面平行, , , 若 , 则( ) A、 B、 C、 D、12. 如果点的坐标满足 , 那么称点为“美丽点”,若某个“美丽点”到轴的距离为 , 则点的坐标为( )A、 B、 C、或 D、或
A、 B、 C、 D、12. 如果点的坐标满足 , 那么称点为“美丽点”,若某个“美丽点”到轴的距离为 , 则点的坐标为( )A、 B、 C、或 D、或二、填空题
-
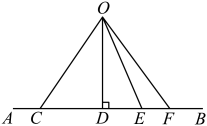
13. 若是二元一次方程的一个解,则m的值为14. 如图,直线外有一点 , 点都在直线上, , 已知 , , , , 则点到直线的距离是 .
 15. 如图所示,若“兵”的位置是 , “炮”的位置是 , 则“将”的位置可以表示为 .
15. 如图所示,若“兵”的位置是 , “炮”的位置是 , 则“将”的位置可以表示为 .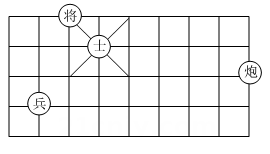 16. 学校为了解本校初一年级学生上学的交通方式,随机抽取了本校20名初一学生进行调查,其中有2名学生是乘私家车上学,如图是收集数据后绘制的扇形图.如果该校初一年级有640名学生,那么骑自行车上学的学生大约有 .
16. 学校为了解本校初一年级学生上学的交通方式,随机抽取了本校20名初一学生进行调查,其中有2名学生是乘私家车上学,如图是收集数据后绘制的扇形图.如果该校初一年级有640名学生,那么骑自行车上学的学生大约有 .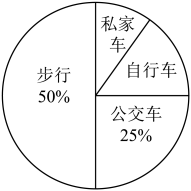 17. 依据图中呈现的运算关系,可知 .
17. 依据图中呈现的运算关系,可知 . 18. 对有理数x , y定义运算: , 其中a , b是常数.如果 , , 那么b的取值范围是 .
18. 对有理数x , y定义运算: , 其中a , b是常数.如果 , , 那么b的取值范围是 .三、解答题
-
19. 计算:;20. 解不等式组 , 并求不等式组的正整数解.21. 如图,在平面直角坐标系中,若三角形是由三角形平移后得到的,且三角形中任意一点经过平移后的对应点为 , 已知: , , .
 (1)、画出三角形;(2)、求三角形的面积;(3)、点在轴上,若三角形的面积为 , 求点的坐标.22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动,在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
(1)、画出三角形;(2)、求三角形的面积;(3)、点在轴上,若三角形的面积为 , 求点的坐标.22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动,在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.活动前骑电瓶车带安全用情况统计表
类别
人数
合计
A:每次带,B:经常带,C:偶尔带,D:都不带.
 (1)、“活动前骑电瓶车戴安全帽情况统计表”中,类别对应人数不小心污损;请求出类别的人数;(2)、若该市约有万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为 , 比活动前增加了人,因此交警部门开展的宣传活动没有效果,请判断小明分析数据的方法是否合理?并结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.23. 【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
(1)、“活动前骑电瓶车戴安全帽情况统计表”中,类别对应人数不小心污损;请求出类别的人数;(2)、若该市约有万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为 , 比活动前增加了人,因此交警部门开展的宣传活动没有效果,请判断小明分析数据的方法是否合理?并结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.23. 【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.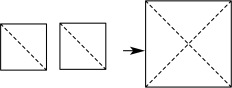 (1)、求大正方形纸片的边长;(2)、若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为 , 且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.24. 阅读理解:
(1)、求大正方形纸片的边长;(2)、若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为 , 且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.24. 阅读理解:在数学课上,李老师遇到下面问题:已知x,y满足方程组 , 求的值?
小红:把方程组解出来,再求的值.
小刚:把两个方程直接相加得方程两边同时除以解得 .
李老师对两位同学的讲解进行点评:指出“小刚”同学的思路体现了数学中【整体思想】的运用.
请你参考小红或小刚同学的做法,解决下面的问题.
(1)、已知关于、的方程组的解满足 , 求的值.(2)、运用【整体思想】解答:若方程组的解是 , 求的值.
25. 年月日上午,伴随着盾构机隆隆轰鸣声,南宁市轨道交通号线“五象火车站一清平坡站”区间盾构顺利始发,标志着号线续建工程正式进入区间据进施工阶段,待此次工程建设完工后,将实现号线全线贯通运营,目前,地铁号线续建工程正在有序进行施工,工地现有大量的泥土需要运输,某车队有载重量为吨、吨的卡车共辆,全部车辆满载运输一次可以运输吨泥土.(1)、求该车队有载重量吨、吨的卡车各多少辆?(2)、随着工程的进展,该车队需要一次运输泥土不低于吨,为了完成任务,该车队准备再购进这两种卡车共辆,则最多购进载重量为吨的卡车多少辆?26. 【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.例如:如图1, , 点、分别在直线、上,点在直线、之间.

求证:;
证明:如图1,过点作 .
,
, ,
,
即: .
【类比应用】已知直线 , 为平面内一点,连接、 .
(1)、如图2,已知 , , 求的度数,请说明理由.(2)、如图3,设、 , 猜想、、之间的数量关系为 .(3)、【联系拓展】如图4,直线 , 为平面内一点,连接、 . , 平分 , 若 , 运用(2)中的结论,直接写出的度数,则的度数为 .