广西壮族自治区南宁市西乡塘区2022-2023学年七年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、3 B、 C、 D、0.12. 下列各组图形可以通过平移一个图形得到另一个图形的是( )A、
 B、
B、 C、
C、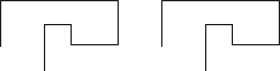 D、
D、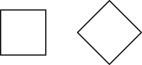 3. 以下调查中,最适宜采用普查方式的是( )A、检测某批次汽车的抗撞击能力 B、调查全国中学生视力和用眼卫生情况 C、调查黄河的水质情况 D、检查我国“神舟十三号”飞船各零部件的情况4. 不等式的解集在数轴上表示正确的是( )A、
3. 以下调查中,最适宜采用普查方式的是( )A、检测某批次汽车的抗撞击能力 B、调查全国中学生视力和用眼卫生情况 C、调查黄河的水质情况 D、检查我国“神舟十三号”飞船各零部件的情况4. 不等式的解集在数轴上表示正确的是( )A、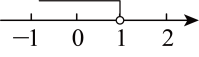 B、
B、 C、
C、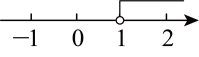 D、
D、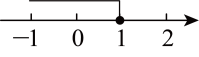 5. 点在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,要把小河里的水引到田地处,则作 , 垂足为 , 沿挖水沟,水沟最短.理由是( )
5. 点在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,要把小河里的水引到田地处,则作 , 垂足为 , 沿挖水沟,水沟最短.理由是( )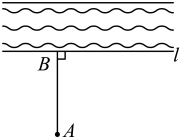 A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点作已知直线的垂线有且只有一条7. 的立方根是( )A、 B、2 C、512 D、8. 已知 ,则下列不等式中不正确的是( )A、 B、 C、 D、9. 方程的解是( )A、 B、 C、 D、10. 如图,下列条件中,能判断的是( )
A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点作已知直线的垂线有且只有一条7. 的立方根是( )A、 B、2 C、512 D、8. 已知 ,则下列不等式中不正确的是( )A、 B、 C、 D、9. 方程的解是( )A、 B、 C、 D、10. 如图,下列条件中,能判断的是( )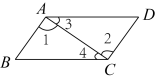 A、 B、 C、 D、11. 《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,动点P按图中箭头所示方向依次运动,从点出发,第1次运动到点 , 第2次运动到点 , 第3次运动到点 , …按这样的运动规律,动点P第2023次运动到点( )
A、 B、 C、 D、11. 《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,动点P按图中箭头所示方向依次运动,从点出发,第1次运动到点 , 第2次运动到点 , 第3次运动到点 , …按这样的运动规律,动点P第2023次运动到点( )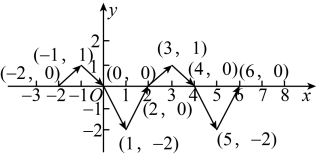 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若电影院中的5排2号记为(5,2),则7排3号记为 .14. 比较大小: 3.(填“>”、“=”或“<”)15. 命题“同位角相等”是(填“真”或“假”,)命题16. 某校调查1000名学生最喜爱的体育活动情况,制成扇形统计图.如图所示,被调查的1000名学生中,最喜欢篮球的有人.
 17. 关于x , y的二元一次方程组的解是 , 其中y的值被墨渍盖住了,则b的值为 .18. 记表示正数x四舍五入后的结果,例如 . 若 , 则x的取值范围是 .19. 【阅读理解】阅读下列解方程组的方法,然后解决问题.
17. 关于x , y的二元一次方程组的解是 , 其中y的值被墨渍盖住了,则b的值为 .18. 记表示正数x四舍五入后的结果,例如 . 若 , 则x的取值范围是 .19. 【阅读理解】阅读下列解方程组的方法,然后解决问题.解方程组时,如果直接考虑消元,那么非常麻烦,而采用下列解法则轻而易举.
解:①+②, ,
即③
①-②,
即
联立③和④,得
解得
所以原方程组的解为
(1)、由二元一次方程组 , 可得; .(2)、解方程组(3)、【拓展提升】对于实数x , y , 定义新运算: , 其中a , b , c是常数,例如: .
已知 , 则 .
三、解答题
-
20. 计算: .21. 解不等式组22. 如图,在平面直角坐标系中,三角形的顶点坐标分别是 , , . 将三角形先向右平移5个单位长度,再向上平移3个单位长度得到三角形 .
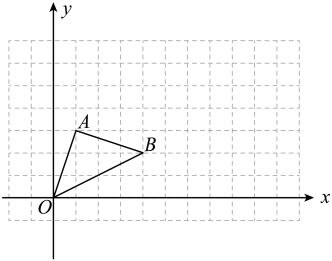 (1)、请画出三角形;(2)、请写出点的坐标 , 点的坐标 , 点的坐标;(3)、求三角形的面积.23. 某校为创建书香校园,倡导读书风尚,开展了师生“大阅读”活动,并制定“大阅读”评选方案,每月评选一次.为了解活动开展情况,学校对全校七年级“大阅读”评选工作进行抽样调查,随机抽取20名学生的“大阅读”积分(分值为整数)情况进行分析.
(1)、请画出三角形;(2)、请写出点的坐标 , 点的坐标 , 点的坐标;(3)、求三角形的面积.23. 某校为创建书香校园,倡导读书风尚,开展了师生“大阅读”活动,并制定“大阅读”评选方案,每月评选一次.为了解活动开展情况,学校对全校七年级“大阅读”评选工作进行抽样调查,随机抽取20名学生的“大阅读”积分(分值为整数)情况进行分析.【收集数据】20名学生的“大阅读”积分(单位:分):
31,40,35,35,12,42,48,25,58,11,26,41,59,40,56,30,49,29,37,40
【整理数据】
积分/分
频数/人次
2
3
5
a
b
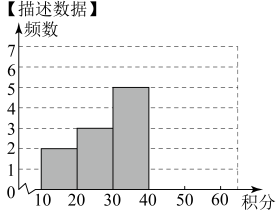
【得出结论】
(1)、填空: , ;(2)、根据表格制成如图所示不完整的频数分布直方图,请将其补全.(3)、学校计划为积分在40分及以上的学生颁发奖状,现七年级共有学生200名,请你估计有多少名学生能够获得奖状?24. 已知:如图,∠1=∠2,∠3=∠E,试说明:∠A=∠EBC(请按图填空,并补充理由):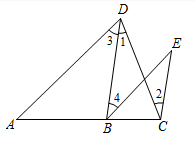
证明:∵∠1=∠2(已知)
∴ ▲ ∥ ▲ , ( )
∴∠E=∠ ▲ , ( )
又∵∠E=∠3(已知)
∴∠3=∠ ▲ , ( )
∴ ▲ ∥ ▲ , (内错角相等,两直线平行)
∴∠A=∠EBC.( )
25. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有四千多年的历史.中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为丰富学生课余生活,计划到甲超市购买一批象棋和围棋.已知购买2副象棋和3副围棋共需140元,购买4副象棋和1副围棋共需130元.(1)、求每副象棋和围棋的单价;(2)、若学校准备购买象棋和围棋共80副,总费用不超过2250元,那么最多能购买多少副围棋?(3)、若甲超市对围棋进行促销:方案一:围棋一律打九折:方案二:办理超市会员卡60元,围棋一律打七折.则学校选用哪种方案购买围棋花费少?26. 如图1,直线被直线所截,直线分别交直线于点A , 点C , 满足 . 将三角形按图1放置,点G在直线上(点G与点A不重合),点M在直线上, .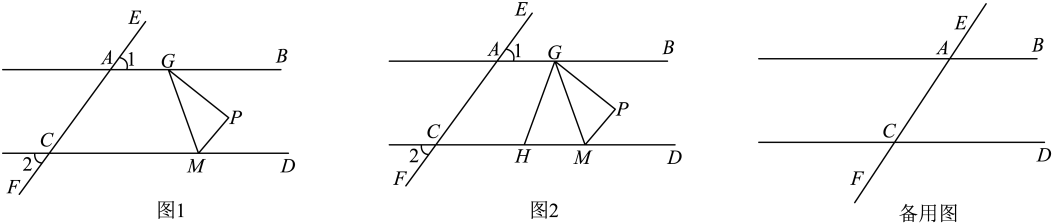 (1)、求证 .(2)、若 , 求的度数.(3)、如图2,的平分线交直线于点H . 现将三角形沿直线平移,请直接写出与的数量关系.
(1)、求证 .(2)、若 , 求的度数.(3)、如图2,的平分线交直线于点H . 现将三角形沿直线平移,请直接写出与的数量关系.