广西壮族自治区南宁市武鸣区2022-2023学年八年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 以下列各组数为边长的三角形,不是直角三角形的是( )A、1,2, B、1,2, C、3,4,5 D、6,8,123. 在函数中,自变量的取值范围是( )A、 B、 C、 D、4. 一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示,你认为商家更应该关注鞋子尺码的( )
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
4
6
6
10
2
1
1
A、平均数 B、中位数 C、众数 D、方差5. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知一次函数的图象如图所示,则取( )时, A、 B、 C、 D、7. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、 B、 C、 D、7. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、甲 B、乙 C、丙 D、丁8. 在▱ABCD中,AB=3cm,AD=4cm,∠A=120°,则▱ABCD的面积是( )A、3 B、6 C、15 D、129. 《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( ) A、 B、 C、 D、10. 如图,矩形纸片中, , 现将其沿对折,使得点落在边上的点处,折痕与边交于点 , 则的长为( )
A、 B、 C、 D、10. 如图,矩形纸片中, , 现将其沿对折,使得点落在边上的点处,折痕与边交于点 , 则的长为( ) A、 B、 C、 D、11. 一个四边形顺次添加下列中的三个条件便得到正方形:
A、 B、 C、 D、11. 一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A、仅① B、仅③ C、①② D、②③12. 如图1,点从四条边都相等的的顶点出发,沿以的速度匀速运动到点 , 图2是点运动时,的面积随时间变化的关系图象,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知直线经过点 , 则的值是 .14. 请写出一个y随x增大而增大的一次函数表达式 .15. 某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是分.16. 已知实数在数轴上的位置如图所示,则化简 .
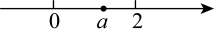 17. 如图所示, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为 .
17. 如图所示, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为 . 18. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
18. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
三、解答题
-
19. 计算: .20. 先化简,再求值: , 其中 .21. 在一次“爱心助学”捐款活动中,全校同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.李老师在全校范围内随机抽取部分学生,对捐款金额进行了统计,根据统计结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
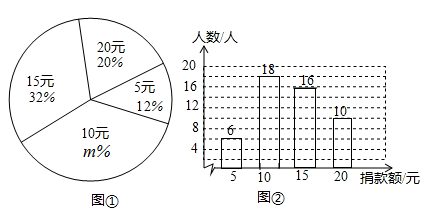 (1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.22. 如图,折线是在某市乘出租车所付车费(元)与行车里程之间的函数关系图象.
(1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.22. 如图,折线是在某市乘出租车所付车费(元)与行车里程之间的函数关系图象. (1)、根据图象,求当时,该图象的函数关系式;(2)、某人乘坐应付多少钱?(3)、若某人付车费30.8元,出租车行驶了多少千米?23. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)、根据图象,求当时,该图象的函数关系式;(2)、某人乘坐应付多少钱?(3)、若某人付车费30.8元,出租车行驶了多少千米?23. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题: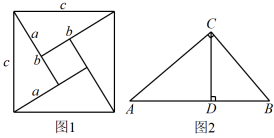 (1)、如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理 .(2)、如图2,在中,是边上的高, , 求的长度;(3)、如图1,若大正方形的面积是13,小正方形的面积是1,求的值 .24. 如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
(1)、如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理 .(2)、如图2,在中,是边上的高, , 求的长度;(3)、如图1,若大正方形的面积是13,小正方形的面积是1,求的值 .24. 如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F. (1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.25. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 , 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.25. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 , 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:类别
价格
款玩偶
款玩偶
进货价(元/个)
40
30
销售价(元/个)
56
45
(1)、第一次小李用1100元购进了 , 两款玩偶共30个,求两款玩偶各购进多少个;(2)、第二次小李进货时,网店规定 款玩偶进货数量不得超过 款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?(3)、小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?(注:利润率 )
26. 在平面直角坐标系中,直线:分别与轴,轴交于点 , , 且与直线:交于点 . (1)、分别求出 , , 三点的坐标.(2)、若是射线上的点,且的面积为12,求直线的函数解析式.(3)、在(2)的条件下,在平面内是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、分别求出 , , 三点的坐标.(2)、若是射线上的点,且的面积为12,求直线的函数解析式.(3)、在(2)的条件下,在平面内是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.