广西南宁市宾阳县2022-2023学年八年级下学期数学期末试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 一组数据:的众数是( )A、 B、 C、 D、3. 勾股定理为勾,为股,为弦 , 若“勾”为 , “股”为 , 则“弦”是( )A、 B、 C、 D、4. 已知一组数据2,x , 4的平均数为3,则x的值是( )A、2 B、3 C、4 D、55. 下列计算错误的是( )A、 B、 C、 D、6. 如图所示,两条公路 , 互相垂直, , 公路的中点M与点C被湖隔开,若测得的长为 , 则M , C两点间的距离为( )
 A、 B、 C、 D、7. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、
A、 B、 C、 D、7. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、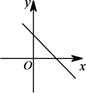 B、
B、 C、
C、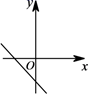 D、
D、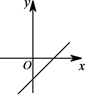 8. 如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
8. 如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( ) A、AB=BC B、∠DAB+∠ABC=180° C、AB=CD,AD=BC D、∠ABC=∠ADC,∠BAD=∠BCD9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )
A、AB=BC B、∠DAB+∠ABC=180° C、AB=CD,AD=BC D、∠ABC=∠ADC,∠BAD=∠BCD9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )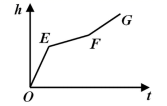 A、
A、 B、
B、 C、
C、 D、
D、 10. 《缉古算经》中记载:“今有五十鹿入舍,小舍容四鹿,大舍容六鹿,需舍几何?”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可容纳6头鹿,若每个圈舍都住满,求需要多少圈舍?设需要大圈舍y间,小圈舍x间,则x与y的方程可列为( )A、 B、 C、 D、11. 如图表示光从空气进入水中前、后的光路图,若按如图建立平面直角坐标系,并设入水前与入水后光线所在直线的表达式分别为 , 则关于与的关系,正确的是( )
10. 《缉古算经》中记载:“今有五十鹿入舍,小舍容四鹿,大舍容六鹿,需舍几何?”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可容纳6头鹿,若每个圈舍都住满,求需要多少圈舍?设需要大圈舍y间,小圈舍x间,则x与y的方程可列为( )A、 B、 C、 D、11. 如图表示光从空气进入水中前、后的光路图,若按如图建立平面直角坐标系,并设入水前与入水后光线所在直线的表达式分别为 , 则关于与的关系,正确的是( ) A、 B、 C、 D、12. 如图,在中, , , , P为边上一动点,于点E , 于点F , 则的最小值为( )
A、 B、 C、 D、12. 如图,在中, , , , P为边上一动点,于点E , 于点F , 则的最小值为( ) A、 B、 C、 D、6
A、 B、 C、 D、6二、填空题
-
13. 若二次根式 在实数范围内有意义,则 的取值范围是.14. 我国最长的河流长江全长约为6 300 000米,6 300 000用科学记数法表示为。15. 将直线向下平移2个单位长度,平移后直线的解析式为 .16. 如图是甲乙两位同学在参加体育中考前的次体能测试成绩折线统计图,由图可知,的成绩更稳定.
 17. 某学校科学兴趣小组为了了解自己育种的树苗的生长情况,随机抽取株树苗测量其高度,统计结果如表:
17. 某学校科学兴趣小组为了了解自己育种的树苗的生长情况,随机抽取株树苗测量其高度,统计结果如表:高度
株数
由此估计这批树苗的平均高度为 .
18. 如图,正方形 , , , …的顶点 , , , …在直线上,顶点 , , , …在x轴上,已知 , , 那么点的坐标为.
三、解答题
-
19. 计算:20. 先化简,再求值: , 其中 .21. 在平面直角坐标系中,一次函数经过 , 两点.
 (1)、直接画出一次函数图象.(2)、求出一次函数解析式.(3)、若函数图象与x轴交于点A , 与y轴交于点B , 求出的面积.22. 电信诈骗,严重危害着人民群众的财产安全,为提高大家的防范意识,某校举行了主题为“防电信诈骗,保财产安全”的知识测试.七、八年级各有700名学生,现从这两个年级各随机抽取50名学生参加测试,为了解本次测试成绩的分布情况,将两个年级的测试成绩x按A: , B: , C: , D:四个评价等级进行整理,得到了不完整的统计图表.七年级成绩统计表:
(1)、直接画出一次函数图象.(2)、求出一次函数解析式.(3)、若函数图象与x轴交于点A , 与y轴交于点B , 求出的面积.22. 电信诈骗,严重危害着人民群众的财产安全,为提高大家的防范意识,某校举行了主题为“防电信诈骗,保财产安全”的知识测试.七、八年级各有700名学生,现从这两个年级各随机抽取50名学生参加测试,为了解本次测试成绩的分布情况,将两个年级的测试成绩x按A: , B: , C: , D:四个评价等级进行整理,得到了不完整的统计图表.七年级成绩统计表:评价等级
成绩x/分
频数
频率
A
25
0.5
B
b
0.02
C
14
0.28
D
10
0.2

八年级测试成绩评价等级为B的全部分数(单位分)如下:
80,80,80,82,83,85,86,87,88,88,89,89,89.
(1)、表格中,;(2)、八年级测试成绩的中位数是 , 八年级测试成绩评价等级为A的人数有人;(3)、若测试成绩不低于80分,则认为该学生对防电信诈骗意识较强,请估计该校七、八两个年级防电信诈骗意识较强的学生一共有多少人?23. 如图,在平行四边形中,过点作于点 , 点在边上, , 连接 , . (1)、求证:四边形是矩形.(2)、已知 , 是的平分线,若 , 求的长度.24. 参观红色基地,研学红色文化.根据校团委的部署,八年级名师生准备租车到革命历史展览馆参观学习.车站有大小两种车型,每辆大车可坐人,每辆小车可坐人,已知租用大车1辆和小车2辆共需元,租用大车2辆和小车1辆共需元.(1)、租大车、小车两种客车每辆各多少元?(2)、若学校计划租辆车,其中大车辆有a辆,租车费用w元,能保障所有的八年级师生到革命历史展览馆参观学习,租车费用不超过元,有哪几种租车方案?租车费用最少为多少?25. 阅读与思考,同学们通过“真阅读工程”活动接触到很多课外阅读,其中有一段文章与勾股定理的内容相关:在直角坐标系中,已知两点的坐标是 , , 求M、N两点之间的距离,可以通过变形为计算.
(1)、求证:四边形是矩形.(2)、已知 , 是的平分线,若 , 求的长度.24. 参观红色基地,研学红色文化.根据校团委的部署,八年级名师生准备租车到革命历史展览馆参观学习.车站有大小两种车型,每辆大车可坐人,每辆小车可坐人,已知租用大车1辆和小车2辆共需元,租用大车2辆和小车1辆共需元.(1)、租大车、小车两种客车每辆各多少元?(2)、若学校计划租辆车,其中大车辆有a辆,租车费用w元,能保障所有的八年级师生到革命历史展览馆参观学习,租车费用不超过元,有哪几种租车方案?租车费用最少为多少?25. 阅读与思考,同学们通过“真阅读工程”活动接触到很多课外阅读,其中有一段文章与勾股定理的内容相关:在直角坐标系中,已知两点的坐标是 , , 求M、N两点之间的距离,可以通过变形为计算.试根据以上知识解决下列问题:
 (1)、若点 , , 则 , 两点间的距离为;(2)、若点与的距离为10,求m的值;(3)、若点 , , 点O是坐标原点,试判断是什么三角形,并说明理由.26.
(1)、若点 , , 则 , 两点间的距离为;(2)、若点与的距离为10,求m的值;(3)、若点 , , 点O是坐标原点,试判断是什么三角形,并说明理由.26. (1)、如图1,四边形是正方形,点G是边的中点, , 且交正方形外角的平分线于点F , 求证:.
(1)、如图1,四边形是正方形,点G是边的中点, , 且交正方形外角的平分线于点F , 求证:.小明展示了一种正确的解题思路:取的中点M , 连接 , 请你写出证明过程.
(2)、如图2,如果把“点G是边的中点”改为“点G是边上(除A、B外)的任意一点”,其他条件不变,那么结论“”仍然成立.这个结论正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(3)、若点G在边的延长线上的任意一点,其他条件不变,结论“.”仍然成立,你认为(1)的结论还正确吗?如果正确,写出证明过程;如果不正确,请说明理由.