浙江省杭州市拱墅区2022-2023学年七年级下学期数学期末试题

试卷更新日期：2023-09-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中，不是 $3 x + 2 y = 10$ 的解的是（）

A、 ${\begin{array}{l} x = 2 \\ \begin{array}{l} y = 2 \end{array} \end{array}$ B、 ${\begin{array}{l} x = - 2 \\ \begin{array}{l} y = 8 \end{array} \end{array}$ C、 ${\begin{array}{l} x = 2 \\ \begin{array}{l} y = 3 \end{array} \end{array}$ D、 ${\begin{array}{l} x = 3 \\ \begin{array}{l} y = \frac{1}{2} \end{array} \end{array}$

查看试题解析
2. 下列等式成立的是（）

A、 $2^{2} \times 2^{3} ＝ 2^{5}$ B、 $2^{2} \times 2^{3} ＝ 2^{6}$ C、 $2^{2} \times 2^{3} ＝ 2^{8}$ D、 $2^{2} \times 2^{3} ＝ 2^{9}$

查看试题解析
3. 多项式 $a x - x$ 因式分解的结果是（）

A、 $a (x - 1)$ B、 $x (a - 1)$ C、a D、 $x (a - x)$

查看试题解析
4. 分式 $\frac{x + 1}{(x - 1) (x^{2} - 4)}$ 有意义，x可取（）

A、 $- 1$ B、1 C、 $- 2$ D、2

查看试题解析
5. 要对大批量生产的商品进行检验，下列做法比较合适的是（）

A、把所有商品逐渐进行检验 B、从中抽取1件进行检验 C、从中挑选几件进行检验 D、从中按抽样规则抽取一定数量的商品进行检验

查看试题解析
6. 一个长方体，它的底面是边长为 $2 a^{3} b$ 的正方形，高为 $3 a b$ ，它的体积是（）

A、 $6 a^{6} b^{3}$ B、 $12 a^{6} b^{3}$ C、 $6 a^{7} b^{3}$ D、 $12 a^{7} b^{3}$

查看试题解析
7. 设A种糖果的单价为每千克a元，B种糖果的单价为每千克10元，则2千克A种糖果和b千克B种糖果混合而成的什锦糖果的单价为每千克（）

A、 $\frac{a + 10}{2}$ 元 B、 $\frac{2 + b}{2}$ 元 C、 $\frac{2 a + 10 b}{2 + b}$ 元 D、 $\frac{2 a + 10 b}{a + 10}$ 元

查看试题解析
8. 分式 $\frac{x^{2} + 2}{x^{2} + 1}$ 的值，可以等于（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
9. 若 $∠ 1$ ， $∠ 2$ ， $∠ 3$ ， $∠ 4$ 的位置如图，则（）

A、 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 360 °$ B、 $∠ 1 + ∠ 2 = ∠ 3 + ∠ 4$ C、 $∠ 1 - ∠ 2 = ∠ 3 - ∠ 4$ D、 $∠ 1 + ∠ 3 = ∠ 2 + ∠ 4$

查看试题解析
10. 设 $a$ ， $b$ 为实数，多项式 $(x + a) (2 x + b)$ 展开后 $x$ 的一次项系数为 $p$ ，多项式 $(2 x + a) (x + b)$ 展开后 $x$ 的一次项系数为 $q$ ：若 $p + q = 6$ ，且 $p$ ， $q$ 均为正整数，则（）

A、 $a b$ 与 $\frac{a}{b}$ 的最大值相等， $a b$ 与 $\frac{a}{b}$ 的最小值也相等 B、 $a b$ 与 $\frac{a}{b}$ 的最大值相等， $a b$ 与 $\frac{a}{b}$ 的最小值不相等 C、 $a b$ 与 $\frac{a}{b}$ 的最大值不相等， $a b$ 与 $\frac{a}{b}$ 的最小值相等 D、 $a b$ 与 $\frac{a}{b}$ 的最大值不相等， $a b$ 与 $\frac{a}{b}$ 的最小值也不相等

查看试题解析

二、填空题

11. 计算2a·3a= .

查看试题解析
12. 要了解某中学七年级（1）班学生的视力情况，比较合适的调查方法是．（填“全面调查”或“抽样调查”中的一个）．

查看试题解析
13. 若不论x为何值， $(x + 1) (x + a) = x^{2} + k x + 6$ ，则 $k =$ ．

查看试题解析
14. 设 $y = a x$ （a为常数），若分式 $\frac{x + y}{x}$ 的值为 $3$ ，则 $a =$ ．

查看试题解析
15. 已知多项式P ， Q的乘积为 $4 a^{2} - b^{2}$ ，若 $P = b - 2 a$ ，则 $Q =$ ．

查看试题解析
16. 如图， $A B ∥ C D$ ，射线 $F E$ ， $F G$ 分别与 $A B$ ， $C D$ 交于点M ， N ，若 $∠ F = ∠ F N D = 3 ∠ E M B$ ，则 $∠ F$ 的度数是．

查看试题解析

三、解答题

17. 解方程组： ${\begin{array}{l} x = 2 y + 3 \\ 2 x + y = 1 \end{array}$ ，并求分式 $\frac{2 y + 3}{1 - 2 x}$ 的值．

查看试题解析
18. 计算：

(1)、 $a (a - 2 b)$ ；

(2)、 ${(- 2 x)}^{3} + 2 x^{3}$ ；

(3)、 $\frac{1}{p - 1} - \frac{1}{p (p - 1)}$ ．

查看试题解析

19. 杭州市教育局为了推动杭州教育领域“共同富裕”探索实践．开展了杭州市中小学“共享优课”赛课活动．拱墅区中学数学教师踊跃参加，上传了初中数学八年级上册

30

节优课．并按优课时长分成

4

组，绘制成如图所示的频数表和未完成的频数分布直方图（每组含前一个边界值，不含后一个边界值）．

上传的八年级上册30节优课时长的频数表

组别（分）	频数
$6.5 - 7.5$	$3$
$7.5 - 8.5$	$9$
$8.5 - 9.5$	$a$
$9.5 - 10.5$	$3$

(1)、求

a

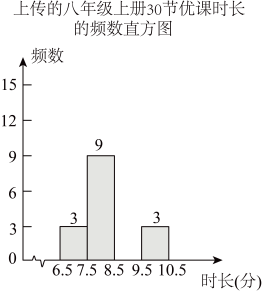的值，并把频数分布直方图补充完整；

(2)、若要播放完这

30

节优课（按正常速度完整播放，不考虑衔接的时间），试通过计算说明：总播放时长超过

4

小时．

查看试题解析

20. 如图， $A B$ $∥$ $C D$ ， $E F$ 分别交 $A B$ ， $C D$ 于点 $G$ ， $H$ ．

(1)、若 $∠ E G B = 70 °$ ，求 $∠ D H F$ 的度数；

(2)、若 $∠ B G H$ 和 $∠ D H G$ 的角平分线交于点 $I$ ，探索 $∠ H G I$ 和 $∠ G H I$ 之间满足的等量关系，说明理由．

查看试题解析
21. 已知多项式① $x^{2} - 2 x y$ ， ② $x^{2} - 4 y^{2}$ ， ③ $x^{2} - 4 x y + 4 y^{2}$ ．

(1)、把这三个多项式因式分解；

(2)、老师问：“三个等式 $① + ② = ③$ ； $① + ③ = ②$ ； $② + ③ = ①$ 能否同时成立？”圆圆同学说：“只有当 $x = y = 0$ 时，三个等式能同时成立，其他x ， y的值都不能使之成立．”你认为圆圆同学的说法正确吗？为什么？

查看试题解析
22. 在一次研究性学习中，同学们对乘法公式进行了研究．

(1)、如图，大正方形的边长为 $(a + b)$ ，直接写出下到结果．
①中间小正方形的边长；
②用含 $a$ ， $b$ 的等式表示：大正方形面积与小正方形面积的差等于图中一个长方形面积的 $4$ 倍．

(2)、当 $x + y = 6$ ， $x - y = - 4$ ．求 $x y$ 的值．

(3)、若当 $x - 2 y = P$ ， $x y = Q$ 时， $(x + 2 y)$ 的值唯一确定，用含 $P$ 的代数式表示 $Q$ ．

查看试题解析
23. 如图，直线 $C D ， E F$ 分别交直线 $A B$ 于点G ， H ，射线 $G I ， H J$ 分别在 $∠ C G B$ 和 $∠ E H B$ 的内部，且 $∠ C G B = 2 ∠ E H B$ ．

(1)、若 $∠ C G B$ 和 $∠ E H B$ 互补．
①求 $∠ E H B$ 的度数；
②当 $∠ C G I = 2 ∠ I G B$ ，且 $G I ∥ H J$ 时，求 $∠ E H J$ 的度数；

(2)、设 $∠ C G I = m ∠ I G B$ ， $∠ E H J = n ∠ J H B$ ．若 $G I ∥ H J$ ，求m ， n满足的等量关系．

查看试题解析