江苏省淮安市2023年中考数学试卷
试卷更新日期:2023-09-28 类型:中考真卷
一、单选题
-
1. 下列实数中,属于无理数的是( )A、﹣2 B、0 C、 D、52. 剪纸是中国优秀的传统文化.下列剪纸图案中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 健康成年人的心脏每分钟流过的血液约 . 数据4900用科学记数法表示为( ).A、 B、 C、 D、4. 下列计算正确的是( ).A、 B、 C、 D、5. 实数在数轴上的对应点的位置如图所示,下列结论正确的是( ).
3. 健康成年人的心脏每分钟流过的血液约 . 数据4900用科学记数法表示为( ).A、 B、 C、 D、4. 下列计算正确的是( ).A、 B、 C、 D、5. 实数在数轴上的对应点的位置如图所示,下列结论正确的是( ).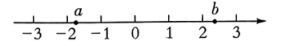 A、 B、 C、 D、6. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ).
A、 B、 C、 D、6. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ). A、 B、 C、 D、7. 如图是一个几何体的三视图,则该几何体的侧面积是( ).
A、 B、 C、 D、7. 如图是一个几何体的三视图,则该几何体的侧面积是( ).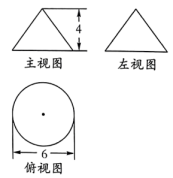 A、 B、 C、 D、8. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点 . 若点坐标为 , 则的值是( ).
A、 B、 C、 D、8. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点 . 若点坐标为 , 则的值是( ).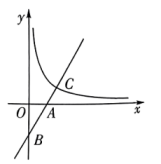 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若式子 在实数范围内有意义,则x的取值范围是 .10. 方程的解是 .11. 若等腰三角形的周长是 , 一腰长为 , 则这个三角形的底边长是 .12. 若 , 则的值是 .13. 将甲、乙两组各10个数据绘制成折线统计图(如图),两组数据的平均数都是7,设甲、乙两组数据的方差分别为 , 则(填“”“=”或“”).
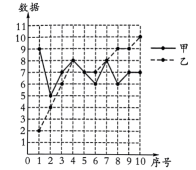 14. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
14. 如图,四边形是的内接四边形,是的直径, , 则的度数是 . 15. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .
15. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .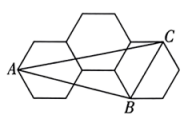 16. 在四边形中,为内部的任一条射线(不等于),点关于的对称点为 , 直线与交于点 , 连接 , 则面积的最大值是 .
16. 在四边形中,为内部的任一条射线(不等于),点关于的对称点为 , 直线与交于点 , 连接 , 则面积的最大值是 .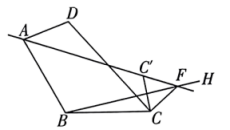
三、解答题
-
17.(1)、计算:;(2)、解不等式组:18. 先化简,再求值: , 其中 .19. 已知:如图,点为线段上一点, , , . 求证: .
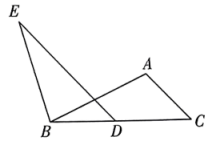 20. 小华、小玲一起到淮安西游乐园游玩,他们决定在三个热门项目(A:智取芭蕉扇、B:三打白骨精、C:盘丝洞)中各自随机选择一个项目游玩.(1)、小华选择C项目的概率是;(2)、用画树状图或列表等方法求小华、小玲选择不同游玩项目的概率.21. 为了调动员工的积极性,商场家电部经理决定确定一个适当的月销售目标,对完成目标的员工进行奖励.家电部对20名员工当月的销售额进行统计和分析.
20. 小华、小玲一起到淮安西游乐园游玩,他们决定在三个热门项目(A:智取芭蕉扇、B:三打白骨精、C:盘丝洞)中各自随机选择一个项目游玩.(1)、小华选择C项目的概率是;(2)、用画树状图或列表等方法求小华、小玲选择不同游玩项目的概率.21. 为了调动员工的积极性,商场家电部经理决定确定一个适当的月销售目标,对完成目标的员工进行奖励.家电部对20名员工当月的销售额进行统计和分析.数据收集(单位:万元):
5.0 9.9 6.0 5.2 8.2 6.2 7.6 9.4 8.2 7.8
5.1 7.5 6.1 6.3 6.7 7.9 8.2 8.5 9.2 9.8
数据整理:
销售额/万元
频数
3
5
4
4
数据分析:
平均数
众数
中位数
7.44
8
问题解决:
(1)、填空: , .(2)、若将月销售额不低于7万元确定为销售目标,则有名员工获得奖励.(3)、经理对数据分析以后,最终对一半的员工进行了奖励.员工甲找到经理说:“我这个月的销售额是7.5万元,比平均数7.44万元高,所以我的销售额超过一半员工,为什么我没拿到奖励?”假如你是经理,请你给出合理解释.22. 为了便于劳动课程的开展,学校打算建一个矩形生态园(如图),生态园一面靠墙(墙足够长),另外三面用的篱笆围成.生态园的面积能否为?如果能,请求出的长;如果不能,请说明理由.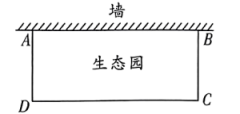 23. 根据以下材料,完成项目任务,
23. 根据以下材料,完成项目任务,
项目任务项目
测量古塔的高度及古塔底面圆的半径
测量工具
测角仪、皮尺等
测量

说明:点为古塔底面圆圆心,测角仪高度 , 在处分别测得古塔顶端的仰角为 , 测角仪所在位置与古塔底部边缘距离 . 点在同一条直线上.
参考数据
(1)、求出古塔的高度.(2)、求出古塔底面圆的半径.24. 如图,在中, . (1)、尺规作图:作 , 使得圆心在边上,过点且与边相切于点(请保留作图痕迹,标明相应的字母,不写作法);(2)、在(1)的条件下,若 , 求与重叠部分的面积.25. 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地卸装货物用时 , 结束后,立即按原路以另一速度匀速返回,直至与慢车相遇,已知慢车的速度为 . 两车之间的距离与慢车行驶的时间的函数图象如图所示.
(1)、尺规作图:作 , 使得圆心在边上,过点且与边相切于点(请保留作图痕迹,标明相应的字母,不写作法);(2)、在(1)的条件下,若 , 求与重叠部分的面积.25. 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地卸装货物用时 , 结束后,立即按原路以另一速度匀速返回,直至与慢车相遇,已知慢车的速度为 . 两车之间的距离与慢车行驶的时间的函数图象如图所示.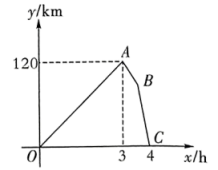 (1)、请解释图中点的实际意义;(2)、求出图中线段所表示的函数表达式;(3)、两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.26. 已知二次函数(为常数).(1)、该函数图象与轴交于两点,若点坐标为 ,
(1)、请解释图中点的实际意义;(2)、求出图中线段所表示的函数表达式;(3)、两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.26. 已知二次函数(为常数).(1)、该函数图象与轴交于两点,若点坐标为 ,①则的值是 ▲ , 点的坐标是 ▲ ;
②当时,借助图像,求自变量的取值范围;
(2)、对于一切实数 , 若函数值总成立,求的取值范围(用含的式子表示);(3)、当时(其中为实数,),自变量的取值范围是 , 求和的值以及的取值范围.27. 综合与实践定义:将宽与长的比值为(为正整数)的矩形称为阶奇妙矩形.
(1)、概念理解:当时,这个矩形为1阶奇妙矩形,如图(1),这就是我们学习过的黄金矩形,它的宽()与长的比值是 .
(2)、操作验证:用正方形纸片进行如下操作(如图(2)):
第一步:对折正方形纸片,展开,折痕为 , 连接;
第二步:折叠纸片使落在上,点的对应点为点 , 展开,折痕为;
第三步:过点折叠纸片,使得点分别落在边上,展开,折痕为 .
试说明:矩形是1阶奇妙矩形.
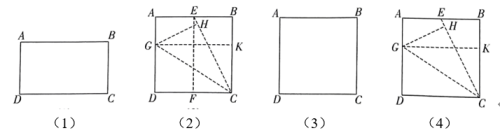 (3)、方法迁移:
(3)、方法迁移:用正方形纸片折叠出一个2阶奇妙矩形.要求:在图(3)中画出折叠示意图并作简要标注.
(4)、探究发现:小明操作发现任一个阶奇妙矩形都可以通过折纸得到.他还发现:如图(4),点为正方形边上(不与端点重合)任意一点,连接 , 继续(2)中操作的第二步、第三步,四边形的周长与矩形的周长比值总是定值.请写出这个定值,并说明理由.