湖北省武汉市黄陂区2022--2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-28 类型:期末考试
一、单选题
-
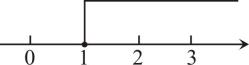
1. 在下列所给出坐标的点中,在第三象限的是( )A、 B、 C、 D、2. 下列调查中,适合全面调查方式的是( )A、了解武汉市空气质量 B、了解武汉市中小学生睡眠时间 C、调查某批次汽车的抗撞击能力 D、了解某班学生新冠病毒疫苗接种情况3. 不等式6﹣2x<0的解集在数轴上表示为( )A、
 B、
B、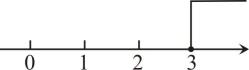 C、
C、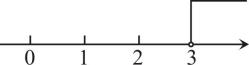 D、
D、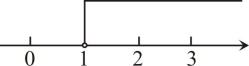 4. 如图,已知 , , , 则的度数是( )
4. 如图,已知 , , , 则的度数是( )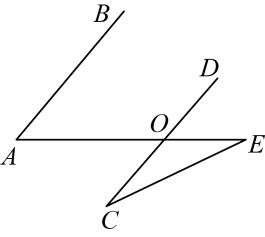 A、 B、 C、 D、5. 若 , 则下列不等式变形正确的是( )A、 B、 C、 D、6. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”意思是:用绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?设绳子长x尺,长木长y尺,则所列方程组正确的是( )A、 B、 C、 D、7. 如果关于x,y的方程组的解中x与y互为相反数,则k的值( )A、9 B、 C、1 D、8. “武汉是座英雄的城市” .在抗击“新冠肺炎”这场没有硝烟的战斗中,广大医务工作者奋战在抗疫的一线前沿是生命中“最美的逆行者”.某方舟医院安排若干名护士负责护理一批新冠病人,若每位护士护理4名病患,有20名患者没有人护理;若安排每位护士护理8名患者,就有一位护士护理的病人多于1人且不足8人.这个方舟医院安排了( )名护士护理新冠病人.A、8 B、7 C、6 D、59. 已知关于x的不等式组 , 下列四个结论:
A、 B、 C、 D、5. 若 , 则下列不等式变形正确的是( )A、 B、 C、 D、6. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”意思是:用绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?设绳子长x尺,长木长y尺,则所列方程组正确的是( )A、 B、 C、 D、7. 如果关于x,y的方程组的解中x与y互为相反数,则k的值( )A、9 B、 C、1 D、8. “武汉是座英雄的城市” .在抗击“新冠肺炎”这场没有硝烟的战斗中,广大医务工作者奋战在抗疫的一线前沿是生命中“最美的逆行者”.某方舟医院安排若干名护士负责护理一批新冠病人,若每位护士护理4名病患,有20名患者没有人护理;若安排每位护士护理8名患者,就有一位护士护理的病人多于1人且不足8人.这个方舟医院安排了( )名护士护理新冠病人.A、8 B、7 C、6 D、59. 已知关于x的不等式组 , 下列四个结论:①若它的解集是 , 则;②当 , 不等式组有解;③若它的整数解仅有3个,则a的取值范围是;④若它有解,则 .
其中正确的结论个数( )
A、1个 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2023个点的坐标为( )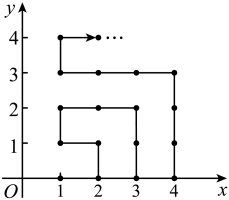 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 比较实数大小:(填“”、“”或“”).12. 体育委员统计了全班女生立定跳远的成绩,列出频数分布表如下:
距离
频数
1
4
8
10
2
已知跳远距离1.8米以上为优秀,则该班女生获得优秀的频率为 .
13. 已知两点 , 的距离为4,且直线轴,则的算术平方根为;14. 把一张对边互相平行的纸条折成如图那样,是折痕,若 , 则;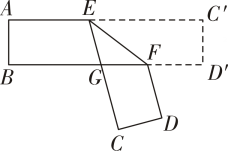 15. 已知关于x,y的方程组的解为 , 则关于m、n的方程组的解为;16. 定义:在平面直角坐标系中,将点变换为(k、b为常数),我们把这种变换称为“T变换”.已知点 , , 经过“T变换”的对应点分别是、F、G.若轴,且点G落在x轴上,则三角形的面积为 .
15. 已知关于x,y的方程组的解为 , 则关于m、n的方程组的解为;16. 定义:在平面直角坐标系中,将点变换为(k、b为常数),我们把这种变换称为“T变换”.已知点 , , 经过“T变换”的对应点分别是、F、G.若轴,且点G落在x轴上,则三角形的面积为 .三、解答题
-
17.(1)、计算:(2)、解方程组:18. 解不等式组,请按下列步骤完成解答:(1)、解不等式①得;(2)、解不等式②得;(3)、把不等式①和②的解集在数轴上表示出来:
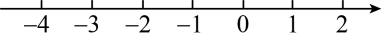 (4)、原不等式组的解集为 .19. 完成下面的推理填空.
(4)、原不等式组的解集为 .19. 完成下面的推理填空.如图,E、F分别在AB和CD上, , 与互余,于G.求证: .
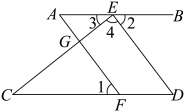
证明:∵
∴( )
∵
∴ ▲ ∥ ▲ ( )
∴( )
∵( )
∴
∵与互余(已知).
∴
∴( )
∴( )
20. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市宣传环保部门为了提高实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,将获得的数据整理绘制成如下两幅不完整的统计图.(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其它垃圾)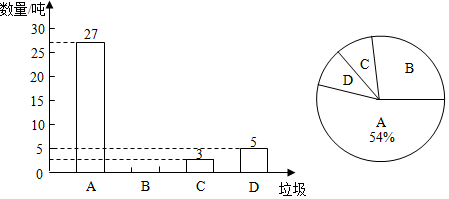
根据统计图提供的信息,解答下列问题:
(1)、在这次抽样调查中,一共有吨的生活垃圾;(2)、请将条形统计图补充完整;(3)、扇形统计图中,B所对应的百分比是 , D所对应的圆心角度数是;(4)、假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,请估计每月产生的有害垃圾多少吨?21. 如图是由边长为1的小正方形组成的网格,每个小正方形的顶点称为格点,已知图中A,B,C三点都是格点,且 , , .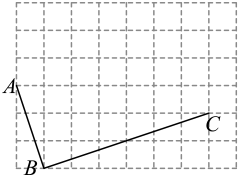 (1)、请在图中画出平面直角坐标系,并直接写出点B的坐标;(2)、P为格点,若三角形的面积为6,则P点的坐标;(3)、将线段平移至 , 使点B与点C重合.
(1)、请在图中画出平面直角坐标系,并直接写出点B的坐标;(2)、P为格点,若三角形的面积为6,则P点的坐标;(3)、将线段平移至 , 使点B与点C重合.①画出线段 , E为线段上一动点,则三角形的面积为 ▲ ;
②若M为上一点,N为上一点,O为坐标原点,当的值最小时,请仅用无刻度的直尺画出点M与点N(保留作图痕迹).
22. “武汉梦时代”为全球最大的纯商业体,总建筑面积约万平方米,该商业体有甲、乙两商场,甲、乙两商场以同样的价格出售同样的商品,并各自推出了优惠方案:在甲商场累计购物金额超过a元后,超出a元的部分按收费;在乙商场累计购物金额超过b元后,超出b元的部分按收费,已知 , 顾客累计购物金额为x元(顾客只能选择一家商场).(1)、若 , ,①当时,到甲商场实际花费元,到乙商场实际花费元;
②若 , 那么当时,到甲或乙商场实际花费一样;
(2)、经计算发现:当时,到甲商场无优惠,而到乙商场则可优惠1元;当时,到甲或乙商场实际花费一样,请求出a,b的值;(3)、若时,到甲或乙商场实际花费一样, , 且 , 请直接写出的最大值 .23. 如图1,点A是直线上一点,C是直线上一点,B是直线之间的一点, .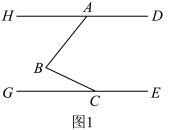 (1)、求证:;(2)、如图2,作 , 与的角平分线交于点F.若 , 求的度数;
(1)、求证:;(2)、如图2,作 , 与的角平分线交于点F.若 , 求的度数;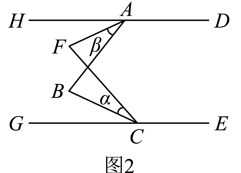 (3)、如图3,平分 , 平分 , , 已知 , 则(直接写出结果).
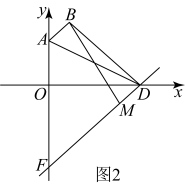
(3)、如图3,平分 , 平分 , , 已知 , 则(直接写出结果).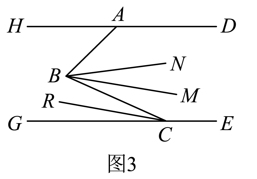 24. 在平面直角坐标系中,设 , , a、b满足 .(1)、直接写出 , .(2)、如图1,直线与x轴交于点C,点N为线段上一点,过点N分别作轴,轴,求;
24. 在平面直角坐标系中,设 , , a、b满足 .(1)、直接写出 , .(2)、如图1,直线与x轴交于点C,点N为线段上一点,过点N分别作轴,轴,求; (3)、如图2,已知点 , 将直线平移至直线 , 且点B的对应点为点D,直线与y轴交于点F,设为线段上一点,且满足三角形的面积不超过三角形面积的 , 直接写出点M的横坐标x的取值范围(不需要解答过程).
(3)、如图2,已知点 , 将直线平移至直线 , 且点B的对应点为点D,直线与y轴交于点F,设为线段上一点,且满足三角形的面积不超过三角形面积的 , 直接写出点M的横坐标x的取值范围(不需要解答过程).