湖北省黄冈市思源系列2023-2024学年八年级上学期开学考试数学试题
试卷更新日期:2023-09-28 类型:开学考试
一、单选题
-
1. 在下面四幅图案中,能通过平移上边图形得到的是( )
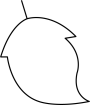 A、
A、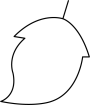 B、
B、 C、
C、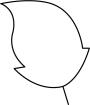 D、
D、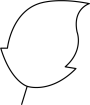 2. 在 , , , , 2022这五个数中无理数的个数为( )A、2 B、3 C、4 D、53. 如图, , ,则 的度数为( )
2. 在 , , , , 2022这五个数中无理数的个数为( )A、2 B、3 C、4 D、53. 如图, , ,则 的度数为( ) A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命5. 若 , 则下列不等式不一定成立的是( )A、 B、 C、 D、6. 将点先向右平移2个单位,再向下平移4个单位,得到的点的坐标为( )A、 B、 C、 D、7. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思就是说,有一群乌鸦要到树林休息,如果每棵树上落坐有三只乌鸦,则有五个落在地上;如果每棵树上落坐有五只乌鸦,则有一棵树没有乌鸦落坐,请你动脑筋,鸦树各几何?若设乌鸦有只,树有棵,由题意可列方程组( )A、 B、 C、 D、8. 非负数x,y满足 , 记 , W的最大值为m,最小值n,则( )A、6 B、7 C、14 D、21
A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命5. 若 , 则下列不等式不一定成立的是( )A、 B、 C、 D、6. 将点先向右平移2个单位,再向下平移4个单位,得到的点的坐标为( )A、 B、 C、 D、7. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思就是说,有一群乌鸦要到树林休息,如果每棵树上落坐有三只乌鸦,则有五个落在地上;如果每棵树上落坐有五只乌鸦,则有一棵树没有乌鸦落坐,请你动脑筋,鸦树各几何?若设乌鸦有只,树有棵,由题意可列方程组( )A、 B、 C、 D、8. 非负数x,y满足 , 记 , W的最大值为m,最小值n,则( )A、6 B、7 C、14 D、21二、填空题
-
9. 要使 有意义,则x的取值范围是 .10. 是连续的两个整数,若 , 则的值为 .11. 一个有80个数据的样本中,样本中的最大值是98,最小值是40,取组距为10,那么这些数据要分成组.12. 如图, , 点E在上,平分 , 若 , 则的度数为°.
 13. 关于x,y的方程组的解满足 , 则m的值为 .14. 如图,将Rt沿着点到的方向平移到的位置,此时 , , 阴影部分面积为40,则平移的距离为 .
13. 关于x,y的方程组的解满足 , 则m的值为 .14. 如图,将Rt沿着点到的方向平移到的位置,此时 , , 阴影部分面积为40,则平移的距离为 .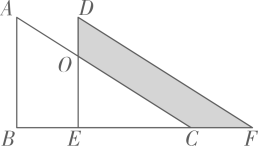 15. 一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是99.原来的两位数是 .16. 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标 , 且x、y均为整数,如数5对应的坐标为 , 则数623对应的坐标是 .
15. 一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是99.原来的两位数是 .16. 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标 , 且x、y均为整数,如数5对应的坐标为 , 则数623对应的坐标是 .
三、解答题
-
17. 解下列方程(组):(1)、;(2)、 .18. 解不等式组 , 并将不等式组的解集表示在数轴上.
 19. 某车间有60名工人,生产甲、乙两种零件,每人每天可以生产24个甲种零件或12个乙种零件.已知每2个甲种零件和3个乙种零件配成一套,问应安排多少名工人生产甲种零件,多少名工人生产乙种零件,才能使每天生产的这两种零件刚好配套?20. 已知:如图,∠D=∠A,∠B=∠FCB
19. 某车间有60名工人,生产甲、乙两种零件,每人每天可以生产24个甲种零件或12个乙种零件.已知每2个甲种零件和3个乙种零件配成一套,问应安排多少名工人生产甲种零件,多少名工人生产乙种零件,才能使每天生产的这两种零件刚好配套?20. 已知:如图,∠D=∠A,∠B=∠FCB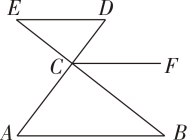
求证:ED//CF
21. 如图在边长为1的正方形网格中,三角形的三个顶点和点D都在格点(网格线的交点)上.其中点A的坐标为 , 平移三角形 , 使点A平移到点D,E、F分别是B、C的对应点.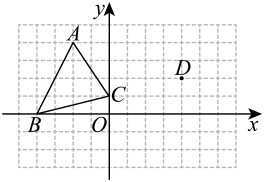 (1)、请画出平移后的三角形 , 并写出点F的坐标.(2)、求三角形的面积.22. 为落实“双减”政策,优化学校作业管理,某校从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间(单位:分钟).按照完成时间分成五组:A组“”,B组“”,组“”,组“”,组“”.将收集的数据整理后,绘制成如下两幅不完整的统计图.
(1)、请画出平移后的三角形 , 并写出点F的坐标.(2)、求三角形的面积.22. 为落实“双减”政策,优化学校作业管理,某校从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间(单位:分钟).按照完成时间分成五组:A组“”,B组“”,组“”,组“”,组“”.将收集的数据整理后,绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、这次调查的样本容量是 ▲ , 并补全条形统计图;(2)、在扇形统计图中,B组的圆心角是度;(3)、若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.23. 某零食店购进A、B两种网红零食共100件,A种零食进价为每件8元,B种零食进价为每件5元,在销售过程中,顾客买了3件A种零食和2件B种零食共付款65元,顾客买了2件A种零食和3件B种零食共付款60元.(1)、求A、B两种零食每件的售价分别是多少元?(2)、若该零食店计划A、B两种零食的进货总投入不超过656元,且销售完后总利润不低于600元,则购进A、B两种零食有多少种进货方案?(3)、在(2)的条件下,哪种进货方案可使获利最大?最大利润是多少元?24. 如图
如图1,在平面直角坐标系中,点A(a,0)在x轴正半轴上,点B(b,c)是第四象限内一点,轴于点C(0,c),且 .
(1)、求点A、B、C三点的坐标;(2)、如图2,D点是线段OC上一动点,交BC于点E,∠ODE的角平分线与∠BAF的角平分线交于第四象限的一点G,AB与DG交于点H,求∠AGD的度数;(3)、如图3,将点C向左平移4个单位得到点H,连接AH,AH与y轴交于点D.①求点D的坐标;
②y轴上是否存在点M,使三角形AHM和三角形AHB的面积相等?若存在,求出点M的坐标;若不存在,请说明理由.