浙江省杭州市上城区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-28 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 若分式有意义,则应满足的条件是( )A、 B、 C、 D、2. 下列四个图形中,与互为内错角的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列方程是二元一次方程的是( )A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 第届亚运会将于年月日至月日在杭州举行本届亚运会共设有个竞赛大项,这个竞赛大项包括个奥运项目和个非奥运项目,其中这个非奥运项目具有浓郁的亚洲特色和中国特色为了调查全校学生最喜爱的亚运竞赛项目情况,下列做法中,比较合理的是( )A、抽取八年级的女生,了解他们最喜爱的亚运竞赛项目 B、抽取七年级的男生,了解他们最喜爱的亚运竞赛项目 C、抽取九年级个班的学生,了解他们最喜爱的亚运竞赛项目 D、三个年级每班随机抽取男生和女生各个,了解他们最喜爱的亚运竞赛项目7. 如图,已知 , , ,则 的度数为( )
3. 下列方程是二元一次方程的是( )A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 第届亚运会将于年月日至月日在杭州举行本届亚运会共设有个竞赛大项,这个竞赛大项包括个奥运项目和个非奥运项目,其中这个非奥运项目具有浓郁的亚洲特色和中国特色为了调查全校学生最喜爱的亚运竞赛项目情况,下列做法中,比较合理的是( )A、抽取八年级的女生,了解他们最喜爱的亚运竞赛项目 B、抽取七年级的男生,了解他们最喜爱的亚运竞赛项目 C、抽取九年级个班的学生,了解他们最喜爱的亚运竞赛项目 D、三个年级每班随机抽取男生和女生各个,了解他们最喜爱的亚运竞赛项目7. 如图,已知 , , ,则 的度数为( )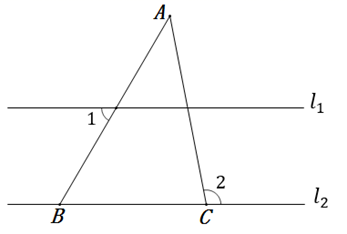 A、50° B、55° C、45° D、60°8. 若关于的分式方程有增根,则常数的值是( )A、 B、 C、 D、9. 如图,面积为的以每秒的速度沿射线方向平移,平移秒后所得图形是点在线段上 , 若 , 则图中的四边形的面积为( )
A、50° B、55° C、45° D、60°8. 若关于的分式方程有增根,则常数的值是( )A、 B、 C、 D、9. 如图,面积为的以每秒的速度沿射线方向平移,平移秒后所得图形是点在线段上 , 若 , 则图中的四边形的面积为( ) A、 B、 C、 D、10. 算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具九章算术的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法各行从左到右列出的算筹数分别表示未知数 , 的系数与相应的常数项把图所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 根据图列出的方程组为( )
A、 B、 C、 D、10. 算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具九章算术的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法各行从左到右列出的算筹数分别表示未知数 , 的系数与相应的常数项把图所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 根据图列出的方程组为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 已知 , 则分式的值是 .12. 方程用含的代数式表示 . .13. 已知是方程组的解,则的值为 .14. 一艘船从处出发,沿南偏东方向行驶至 , 然后向正东方向行驶至后又改变航向,朝与出发时相反的方向行驶至 , 则的度数为 .15. 如果是一个完全平方式,则 .16. 生活中我们经常用到密码,如手机解锁、密码支付等为方便记忆,有一种用“因式分解”法产生的密码,其原理是:将一个多项式分解成多个因式,如:将多项式分解结果为当时, , , 此时可得到数字密码将多项式因式分解后,利用题目中所示的方法,当时可以得到密码 , 则 .
三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 按要求计算:(1)、;(2)、;(3)、分解因式: .18. 解下列方程组:(1)、;(2)、 .19. 为了响应教育部关于中小学学生近视眼防控工作方案的文件,某校为了解学生视力状况,从全校名学生中,随机抽取了其中名学生进行视力检查,并根据调查结果,将学生分为、、、、五个等级,其中表示超级近视、表示严重近视、表示中等近视、表示轻微近视、表示视力良好,并绘制两幅不完整的统计图表某校抽取学生视力检查结果的频数表:
等级
视力
人数
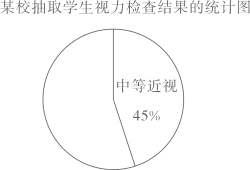
请结合题中信息,解答下列问题:
(1)、下列判断不正确的是____;A、名学生的视力是总体; B、样本容量是; C、名学生的视力是样本; D、每名学生的视力是个体.(2)、表中 , ;(3)、学校准备采取措施治疗和干预近视程度为“中等”和“严重”的学生,请你估计大约一共有多少人.20.(1)、先化简,再求值: , 其中;(2)、先化简,再求值: , 并从 , , , 中选取一个合适的数作为的值代入求值.21. 如图,已知 , 平分 , . (1)、求证:;(2)、若 , , 求的度数.22. 杭州亚运会篮球比赛,目前推出两种观赛门票,价格为:类票元张,类票元张杭州某企业计划投入万元,全部用于购买篮球比赛门票两类门票都有 , 用作职工福利.(1)、若购买门票总数为张,求购买的类票和类票分别的张数;(2)、若购买门票总数张,其中类票张.
(1)、求证:;(2)、若 , , 求的度数.22. 杭州亚运会篮球比赛,目前推出两种观赛门票,价格为:类票元张,类票元张杭州某企业计划投入万元,全部用于购买篮球比赛门票两类门票都有 , 用作职工福利.(1)、若购买门票总数为张,求购买的类票和类票分别的张数;(2)、若购买门票总数张,其中类票张.①求与满足怎样的数量关系;
②若购买的门票中类票比类票的倍还多张,求类门票的张数.
23. 综合实践.活动主题:探究图形面积与代数式之间的关系
活动资源:提供长度不同的两种木棒各根如图

入项任务:运用以上根木棒不折断摆成长方形或正方形,且木棒全部用完选取同学们的甲、乙、丙、丁四种不同的摆法如图进行研究.

问题探究过程
(1)、发现问题:请观察以上所有图形,并研究不同2种或2种以上摆法的图形面积之间关系,你发现哪些结论?
例如:小明发现:甲摆法的面积是乙摆法总面积的2倍.
小张发现:丁摆法的总面积大于乙摆法的总面积.
聪明的你,能提出不同于小明和小张的更创新更有意义问题吗?
你的发现是;请用简洁的语言描述
(2)、提出问题:请用代数式表示你的发现设两种木棒的长度分别为 , 其中 , 四种图形面积分别为 , , , .
例如:小明的结论是 .
小张的结论是 ,
你的结论是:;
(3)、分析问题:请用所学的数学知识证明你的结论.
例如:小明的证明方法如下.
证: , ,
,
你的证明:;
(4)、拓展创新:把甲摆法围成大长方形纸片沿虚线剪成四个全等的小长方形,请用四个小长方形拼摆出边长为的正方形,画出示意图,并用等式表达示意图中的各图形面积之间的关系.
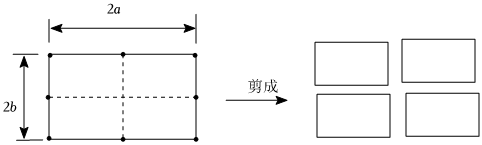
你的示意图:;
你的关系式: .
(5)、迁移应用:根据以上的研究结论,请解决数学问题,若 , , 求的值.
你的解答: .