浙江省杭州市西湖区2023年中考三模数学试卷

试卷更新日期：2023-09-28 类型：中考模拟

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 在下列实数中，属于无理数的是（）

A、 $\frac{1}{2023}$ B、-0.2023 C、2023 D、 $\sqrt{2023}$

查看试题解析
2. 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食物和药物，得到广泛的使用．经测算，一粒芝麻的质量约为0.00000209kg ，将0.00000209用科学记数法表示为（）

A、2.09×10^-8 B、0.209×10^-7 C、2.09×10^-6 D、20.9×10^-5

查看试题解析
3. 如图所示的几何体是由一个圆锥体和一个圆柱体组成的，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 一个多边形的内角和是外角和的3倍，则这个多边形的边数（）

A、9 B、8 C、7 D、6

查看试题解析
5. 设x ， y ， c为实数，则下列说法正确的是（）

A、若x＞y ，则x+3c＞y-2c B、若x＞y ，则xc＞yc C、若x＞y ，则xc²＞yc² D、若 $\frac{x}{c^{2}} > \frac{y}{c^{2}}$ ，则x＞y

查看试题解析
6. 设A（x₁ ， y₁）B（x₂ ， y₂）是反比例函数 $y = \frac{3}{x}$ 图象上的两点．若x₁＜x₂＜0，则y₁与y₂之间的关系是（）

A、y₂＞y₁＞0 B、y₁＞y₂＞0 C、y₁＜y₂＜0 D、y₂＜y₁＜0

查看试题解析
7. 如图，Rt△ABC中， ∠ACB=90°，∠A=30°，CD⊥AB于D，CE是△ABC的中线，要说明“三个角分别对应相等的两个三角形全等”是假命题，可以作为反例的两个三角形是（）

A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD

查看试题解析
8. 《九章算术》是中国古代数学著作之一，书中有这样的一个问题：五只雀，六只燕共重一斤，雀重燕轻，互换一只，恰好一样重．问：每只雀、燕的重量各为多少？设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
9. 如图，在圆内接正六边形ABCDEF中，BF ， BD分别交AC于点G ， H ，若该圆的半径为12，则线段GH的长为（）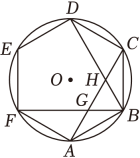

A、6 B、 $4 \sqrt{3}$ C、 $5 \sqrt{2}$ D、8

查看试题解析
10. 已知二次函数y＝a（x-k）（x+k-6），当x＝x₁时，函数值为y₁ ，当x＝x₂时，函数值为y₂ ，若|x₁-3|＜|x₂-3|，则下列结论正确的是（）

A、y₁-y₂＜0 B、a（y₁-y₂）＜0 C、y₁+y₂＞0 D、a（y₁+y₂）＞0

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

11. 计算：3⁰＝； $\sqrt{{(- 2)}^{2}}$ ＝．

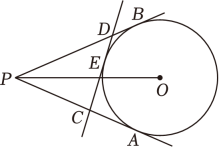
查看试题解析
12. 分解因式：2m²﹣18= ．

查看试题解析
13. 在一个布袋里放有1个白球和2个红球，它们除颜色外其余都相同，从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球．则两次摸出的球都是红球的概率是．

查看试题解析
14. 有一个圆心角为120°，半径长为9cm的扇形，若将其围成一圆锥侧面，那么这个圆锥的底面圆的半径是cm．

查看试题解析
15. 如图，PA ， PB分别与半径为3的⊙O相切于点A ， B ，直线CD分别交PA ， PB于点C ， D ，并切⊙O于点E ，当PO＝6时，△PCD的周长为．

查看试题解析
16. 如图，在矩形ABCD中，点E是AD的中点，连接BE ，将△ABE沿着BE翻折得到△FBE ， EF交BC于点H ，延长BF ， DC相交于点G ，若DG＝8，BC＝12，则AB＝， EH＝．

查看试题解析

三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算

17. 以下是圆圆同学化简 $\frac{2 a}{a^{2} - 9} - \frac{1}{a - 3}$ 的解答过程：
解：原式＝ $\frac{2 a}{(a + 3) (a - 3)} - \frac{1}{a - 3} = 2 a - a + 3 = a + 3$

圆圆的解答是否有错误？如果有错误，请写出正确的解答过程．

查看试题解析

18. 某校为了解九年级各班男生引体向上情况，随机抽取两个班各6名同学进行测试，其有效次数分别为：九（1）班：6，8，8，8，8，10；九（3）班：10，4，8，6，10，10．现从平均数、众数、中位数、方差对两个班做如下分析：

	平均数	众数	中位数	方差
九（1）班	8	8	8	4
九（3）班	8	a	b	c

(1)、求a ， b ， c的值；

(2)、如果引体向上有效次数10次的成绩为满分，请以这12名同学的成绩为样本，估计该校九年级240名男生引体向上成绩达到满分的人数．

查看试题解析

19. 如图，在等边△ABC中，D ， E分别是AB ， BC上的点，且BD＝CE ，连接AE ， CD交于点F ．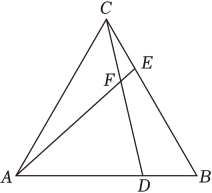

(1)、求证：△ACE≌△CBD；

(2)、求∠AFD的正弦值．

查看试题解析
20. 已知一次函数y₁＝kx+b与反比例函数 $y_{2} = \frac{m}{x}$ ，

(1)、若函数y₁与函数y₂的图象交于点A（3，2），点B（-1，a），
①求一次函数和反比例函数的表达式；
②当y₁＞y₂时，直接写出x的取值范围；

(2)、若点C（3，k）在函数y₁的图象上，求函数y₁的图象经过的定点．

查看试题解析
21. 如图，以△ABC的一边AB为直径作⊙O ， ⊙O与BC边的交点D恰好为BC的中点，DE⊥AC ．

(1)、求证：DE为圆O的切线；

(2)、连接OC交DE于点F ，若 $c o s ∠ A B C = \frac{3}{8}$ ，求 $\frac{O F}{F C}$ 的值．

查看试题解析
22. 在平面直角坐标系中，设二次函数 $y_{1} = x^{2} - 3 a x + 1$ （a是常数）

(1)、当a＝2时，求函数y₁图象的顶点坐标和对称轴；

(2)、若函数y₁图象经过点（1，p），（-1，q），求证：pq≤4；

(3)、若a＜0，y₂＝x-3a+1，y₁ ， y₂的图象交于点（x₁ ， m）（x₂ ， n），（x₁＜x₂），设（x₃ ， n）为y₁图象上一点（x₃≠x₂），求x₃-x₁的值．

查看试题解析
23. 正方形ABCD的边长为1，连接BD ，过点C作BD的平行线CE ， BE与CD相交于点F ，过点D作DH⊥BE ．

(1)、求△BDE的面积；

(2)、当∠CBE＝15°时，求BE的长；

(3)、若△EFC的面积记为S₁ ， △DFH的面积记为S₂ ， △DBF的面积记为S₃ ， △BFC的面积记为S₄ ， $\frac{C F}{C D} = k$ ，请用k的代数式表示 $\frac{S_{1} \cdot S_{2}}{S_{3} \cdot S_{4}}$ 的值．

查看试题解析