浙江省温州市2022-2023学年年九年级上册数学学业水平开学检测试卷

试卷更新日期：2023-09-28 类型：开学考试

进入出卷网下载

一、选择题(本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，选择正确才给分)

1. 下列函数中，① $y = 2 x$ ；② $y = 2 - x$ ；③ $y = - \frac{2}{x}$ ；④ $y = x^{2} + 6 x + 8$ .函数图象经过第四象限的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 从长度分别为 $1 c m$ 、 $3 c m$ 、 $5 c m$ 、 $6 c m$ 四条线段中随机取出三条，能够组成三角形的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
3. 一个不透明的袋中有四张完全相同的卡片，把它们分别标上数字1、2、3、4．随机抽取一张卡片，然后放回，再随机抽取一张卡片，则两次抽取的卡片上数字之积为偶数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、 $\frac{5}{6}$

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 7$ ， $B C = 24$ ，将它绕着 $B C$ 中点 $D$ 顺时针旋转一定角度后到 $△ A^{'} B^{'} C^{'}$ ，恰好使 $B^{'} C^{'} / / A B$ ， $A^{'} C^{'}$ 与边 $A B$ 交于点 $E$ ，则 $A^{'} E$ 的长为（）

A、 $\frac{7}{2}$ B、 $\frac{49}{24}$ C、 $\frac{84}{25}$ D、 $\frac{91}{25}$ 。

查看试题解析
5. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，现有以下结论：（1） $b > 0$ ：（2） $a b c < 0$ ；（3） $a - b + c > 0$ ，（4） $a + b + c > 0$ ；（5） $b^{2} - 4 a c > 0$ ；其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个．

查看试题解析
6. 我校门口道路的隔离栏通常会涂上醒目的颜色，呈抛物线形状，如图是一个长为2米，宽为1米的矩形隔离栏，中间被4根栏杆五等分，每根栏杆的下面一部分涂上醒目的蓝色，颜色的分界处（点E ，点P）以及点A ，点B落上同一条抛物线上，若第1根栏杆涂色部分（EF）与第2根栏杆未涂色部分（PQ）长度相等，则EF的长度是（）

A、 $\frac{1}{3}$ 米 B、 $\frac{1}{2}$ 米 C、 $\frac{2}{5}$ 米 D、 $\frac{3}{5}$ 米

查看试题解析
7. 二次函数y＝ax²＋bx＋c的图象如图所示，则函数y＝bx＋c的图象和函数y＝ $\frac{a + b + c}{x}$ 的图象在同一坐标系中大致为（）

A、 B、 C、 D、

查看试题解析
8. 三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小完全相同．当水面刚好淹没小孔时，大孔水面宽度为10米，孔顶离水面1.5米；当水位下降，大孔水面宽度为14米时，单个小孔的水面宽度为4米，若大孔水面宽度为20米，则单个小孔的水面宽度为（）

A、4 $\sqrt{3}$ 米 B、5 $\sqrt{2}$ 米 C、2 $\sqrt{13}$ 米 D、7米

查看试题解析
9. 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC、BC为直径作半圆，其中M，N分别是AC、BC为直径作半圆弧的中点， $\overset{⌢}{A C}$ ， $\overset{⌢}{B C}$ 的中点分别是P，Q.若MP+NQ＝7，AC+BC＝26，则AB的长是（）

A、17 B、18 C、19 D、20

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = \sqrt{5}$ .以 $A B$ 为直径作 $⊙ O$ ，作直径 $C D$ ，连结 $A D$ 并延长至点E，使 $D E = A D$ ，连结 $C E$ 交 $A B$ 于点F， $D G / / A B$ 交 $C E$ 于点G.若 $A C = 2 E G$ ，则直径 $A B$ 的长为（）

A、 $3 \sqrt{2}$ B、 $\sqrt{19}$ C、 $2 \sqrt{5}$ D、 $\sqrt{21}$

查看试题解析

二、填空题(本题共8小题，共40分，标明“㉿”符号题目在学校要求下选择是否与附加题替换，替换后需写附加题，不替换需写原题)

11. 一布袋里装有4个红球、5个黄球、6个黑球，这些球除颜色外其余都相同，那么从这个布袋里摸出一个黄球的概率为．

查看试题解析
12. 关于x的方程 $\sqrt{2 x - 4} - \sqrt{x + a} = 1$ 有一个增根 $x = 4$ ，则 $a =$ ．

查看试题解析
13. 已知抛物线 $y = x^{2} - x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $- 3 m^{2} + 3 m + 2022$ 的值为．

查看试题解析
14. 如图，抛物线 $y = a (x + 1) (x - 3)$ 与x轴交于A ， B两点（点A在B的左侧），点C为抛物线上任意一点（不与A ， B重合）， $B D$ 为 $△ A B C$ 的 $A C$ 边上的高线，抛物线顶点 $E$ 与点 $D$ 的最小距离为1，则抛物线解析式为．

查看试题解析
15. 如图，矩形ABCD中，AB＝2，AD＝4，E为BC的中点，F为DE上一动点，P为AF中点，连接PC，则PC的最小值是.

查看试题解析
16. 如图，纸片▱ABCD面积为6，AB＝3，∠BAD＝45°，按下列步骤进行裁剪和拼图．
第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开（E为BD上任意一点），得到△ABE和△ADE纸片；
第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处（边PQ与DC重合，△PQM和△DCF在DC同侧），将△BCG纸片翻转过来使其背面朝上置于△PRN处，（边PR与BC重合，△PRN和△BCG在BC同侧）．
由此可知，由纸片拼成的五边形PMQRN中，对角线MN长度的最小值为．

查看试题解析
17. 如图所示。小林家的洗手盘台面上有一瓶洗手液（如图1）．当手按住顶部A下压如图2位置时，洗手液瞬间从喷口B流出路线呈抛物线经过C与E两点．瓶子上部分是由弧 $\overset{⌢}{C E}$ 和弧 $\overset{⌢}{F D}$ 组成，其圆心分别为D，C．下部分的是矩形CGHD的视图，GH＝10cm，点E到台面GH的距离为14cm，点B距台面的距离为16cm，且B，D，H三点共线．若手心距DH的水平距离为2cm去接洗手液时，则手心距水平台面的高度为cm．

查看试题解析
18. ㉿已知半径为 $r$ 的 $⊙ O$ 是矩形 $A B C D$ 的外接圆，点 $E$ 是弧 $A B$ 上的一点，分别延长 $B E$ ， $D A$ 交于点 $F$ ，其中 $A D = 3$ ．如图甲，当点 $E$ 是弧 $A B$ 的中点时， $A F =$ （用 $r$ 的代数式表示）；如图乙，当点 $E$ 是弧 $A C$ 的中点时，且 $S_{△ A E F} = 10$ ， $r$ 的值为．

查看试题解析

三、解答题(本题共6小题，共70分，无特定要求的解答时需写出必要的文字说明，演算步骤或证明过程)

19. 计算：先化简，再求值： $(1 - x + \frac{2 x - 1}{x + 1}) \div \frac{x - 2}{x^{2} + 2 x + 1}$ ，其中x的值是方程 $x^{2} + x - 6 = 0$ 的解．

查看试题解析
20. 如图，在每个小正方形的边长均为1的方格纸中，有线段 $A B$ 和线段 $C D$ ，点 $A$ 、 $B$ 、 $C$ 、 $D$ 均在小正方形的顶点上．

(1)、在方格纸中画出以 $A B$ 为对角线的正方形 $A E B F$ ，点 $E$ 、 $F$ 在小正方形的顶点上；

(2)、在方格纸中画出以 $C D$ 为斜边的等腰直角三角形 $C D M$ ，点 $M$ 在小正方形的顶点上，连接 $M B$ ，请直接写出 $M B$ 长＝ ▲ ．

查看试题解析
21. 6月13日，某港口的潮水高度y（ $c m$ ）和时间x（h）的部分数据及函数图象如下：(数据来自某海洋研究所)

(1)、数学活动：
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．
②观察函数图象，当 $x = 4$ 时，y的值为多少？当y的值最大时，x的值为多少？ ▲ ， ▲ .

(2)、数学思考：
结合函数图象，写出该函数的两条性质或结论．

x(h)
…
11
12
13
14
15
16
17
18
…
y(cm)
…
189
137
103
80
101
133
202
260
…

(3)、数学应用：
当潮水高度超过260 $c m$ ，货轮能安全进出港口．问当天货轮进出港口最佳时间段？

查看试题解析
22. 某教育部门为了解本地区中小学生参加家庭劳动时间的情况，随机抽取该地区1200名中小学生进行问卷调查，并将调查问卷（部分）和结果描述如下：
中小学生每周参加家庭劳动时间x（h）分为5组：第一组（0≤x<0.5），第二组（0.5≤x<1），第三组（1≤x<1.5），第四组（1.5≤x<2），第五组（x≥2）．根据以上信息，解答下列问题：

(1)、本次调查中，中小学生每周参加家庭劳动时间的中位数落在哪一组？

(2)、在本次被调查的中小学生中，选择“不喜欢”的人数为多少？

(3)、该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于2h，请结合上述统计图，对该地区中小学生每周参加家庭劳动时间的情况作出评价，并提出两条合理化建议．
.

查看试题解析
23. 某商品的成本（单位：百元）由包装费和生产费两部分组成．其中当原料数量（单位：千克）低于4千克时，包装费 $y_{1}$ （单位：百元）与原料数量之间的关系式为 $y_{1} = 1.2 - 0.3 x$ ；当原料数量不低于4千克时，包装费全免．生产费 $y_{2}$ （单位：百元）与原料数量之间的关系式为： $y_{2} = a x^{2} + 0.1 x (a > 0)$ ．

(1)、当原料数量 $x = 3$ 时，该商品的成本为：（百元）；当原料数量 $x = 5$ 时，该商品的成本为：（百元）；（直接用含的式子表示）

(2)、若 $a = 0.1$ ，求原料数量为多少千克时，该商品的成本最少？最少是多少百元？

(3)、当原料数量低于4千克时，有且仅有唯一正整数使得该商品的成本不高于2百元，直接写出的取值范围．

查看试题解析
24. 如图1，矩形 $A B C D$ 中， $A B = 6 ， A D = 8$ ，点P在边 $B C$ 上，且不与点B、C重合，直线 $A P$ 与 $D C$ 的延长线交于点E ．

(1)、当点P是 $B C$ 的中点时，求证： $△ A B P ≌ △ E C P$ ；

(2)、将 $△ A P B$ 沿直线 $A P$ 折叠得到 $△ A P B^{'}$ ，点 $B^{'}$ 落在矩形 $A B C D$ 的内部，延长 $P B^{'}$ 交直线 $A D$ 于点F ．
①证明 $F A = F P$ ，并求出在（1）条件下 $A F$ 的值；
②连接 $B^{'} C$ ，求 $△ P C B^{'}$ 周长的最小值；

(3)、如图2， $B B^{'}$ 交 $A E$ 于点H ，点G是 $A E$ 的中点。当 $∠ E A B^{'} = 2 ∠ A E B^{'}$ 时，请判断 $A B$ 与 $H G$ 的数量关系为 ▲ ，并说明理由．

查看试题解析

四、附加题(本题共2小题，共10分)

25. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD为 $∠ B A C$ 的平分线，将AB绕点B逆时针旋转90°得到BE ， $E F ⊥ A D$ ，垂足为F ， EF与AB交于点G ．

(1)、求证： $∠ B A D = ∠ E$ ；

(2)、求 $∠ B F E$ 的度数；

(3)、求证： $E F = A F + B C$ ．

查看试题解析
26. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A C$ 为 $⊙ O$ 的直径， $∠ A D B = ∠ C D B$ ．

(1)、试判断 $△ A B C$ 的形状，并给出证明；

(2)、若 $A B = \sqrt{2}$ ， $A D = 1$ ，求 $C D$ 的长度．

查看试题解析

五、思维扩展(本题共9小题，共50分，分为选择题，填空题与解答题)

27. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，有下列说法：
①若 $a - b + c = 0$ ，则方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 必有一个根为1；

②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 必有两个不相等的实根；

③若 $c$ 是方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；

④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} - b)}^{2}$ ．

其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
28. 清代著名数学家梅文鼎在《勾股举隅》一书中，用四个全等的直角三角形拼出正方形 $A B C D$ 的方法证明了勾股定理（如图）．设四个全等直角三角形的较短直角边为 $a$ ，较长直角边为 $b$ ，五边形 $B C D E F$ 的面积为 $S_{1}$ ， $Δ F G H$ 的面积为 $S_{2}$ ，若 $a = 1$ ， $\frac{S_{1}}{S_{2}} = \frac{7}{5}$ ，则 $b$ 的值为（）

A、5 B、6 C、7 D、8

查看试题解析
29. 如图，▱ABCD中，AB＝3，AD＝5，AC⊥AB ， E、F为线段BD上两动点（不与端点重合）且EF＝ $\frac{1}{2}$ BD ，连接AE ， CF ，当点EF运动时，对AE+CF的描述正确的是（）

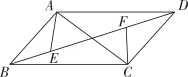A、等于定值5- $\sqrt{2}$ B、有最大值 $\frac{12 \sqrt{13}}{13}$ C、有最小值 $\frac{12 \sqrt{13}}{13}$ D、有最小值 $\sqrt{13}$

查看试题解析
30. 如图1，在矩形ABCD中，AB＜BC ， AC ， BD交于点O ．点E为线段AC上的一个动点，连接BE ， DE ，过点E作EF⊥BD于点F ．设图1中一线段的长为x ， DE＝y ，表示y与x的函数关系的图象如图2所示，则这条线段可能是图1中的（）

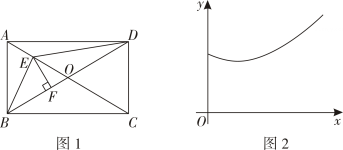A、线段FE B、线段CE C、线段BE D、线段AE

查看试题解析
31. 如图，在平面直角坐标系中，矩形 $A B C D$ 的对角线 $A C$ 的中点与坐标原点重合，点E是x轴上一点，连接 $A E$ .若 $A D$ 平分 $∠ O A E$ ，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过 $A E$ 上的两点A ， F ，且 $A F = E F$ 的面积为9，则k的值为（）

A、3 B、6 C、9 D、12

查看试题解析
32. 如图，△ABC是等腰三角形，AB＝AC ， ∠B＝30°，△ADE是直角三角形，∠ADE＝90°，∠E＝30°，AD＝AB ．将△ADE绕点A旋转，AD、AE分别交BC于点F ， G ，当∠AGB＝75°时， $\frac{F G}{D E} =$ ．

查看试题解析
33. 对于任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[ $\sqrt{3}$ ]=1．现对72进行如下操作：72 $\underset{\to}{第一次}$ [ $\sqrt{72}$ ]=8 $\underset{\to}{第二次}$ [ $\sqrt{8}$ ]=2 $\underset{\to}{第三次}$ [ $\sqrt{2}$ ]=1，类似地，只需进行3次操作后变为1的所有正整数中，最大的是．

查看试题解析
34. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C = 2 \sqrt{2}$ ， D为 $B C$ 的中点，E ， F分别为 $A C$ ， $A D$ 上任意一点，连接 $E F$ ，将线段 $E F$ 绕点E顺时针旋转90°得到线段 $E G$ ，连接 $F G$ ， $A G$ ．

(1)、如图1，点E与点C重合，且 $G F$ 的延长线过点B ，若点P为 $F G$ 的中点，连接 $P D$ ，求 $P D$ 的长；

(2)、如图2， $E F$ 的延长线交 $A B$ 于点M ，点N在 $A C$ 上， $∠ A G N = ∠ A E G$ 且 $G N = M F$ ，求证： $A M + A F =$ $\sqrt{2} A E$ ；

(3)、如图3，F为线段 $A D$ 上一动点，E为 $A C$ 的中点，连接 $B E$ ， H为直线 $B C$ 上一动点，连接 $E H$ ，将 $△ B E H$ 沿 $E H$ 翻折至 $△ A B C$ 所在平面内，得到 $△ B' E H$ ，连接 $B' G$ ，直接写出线段 $B' G$ 的长度的最小值．

查看试题解析
35. 如图1，抛物线 $y = a x^{2} + 2 x + c$ 经过点 $A (- 1 ， 0) 、 C (0 ， 3)$ ，并交x轴于另一点B ，点 $P (x ， y)$ 在第一象限的抛物线上， $A P$ 交直线 $B C$ 于点D ．

(1)、求该抛物线的函数表达式；

(2)、当点P的坐标为 $(1 ， 4)$ 时，求四边形 $B O C P$ 的面积；

(3)、点Q在抛物线上，当 $\frac{P D}{A D}$ 的值最大且 $△ A P Q$ 是直角三角形时，求点Q的横坐标；

(4)、如图2，作 $C G ⊥ C P ， C G$ 交x轴于点 $G (n ， 0)$ ，点H在射线 $C P$ 上，且 $C H = C G$ ，过 $G H$ 的中点K作 $K I ∥ y$ 轴，交抛物线于点I ，连接 $I H$ ，以 $I H$ 为边作出如图所示正方形 $H I M N$ ，当顶点M恰好落在y轴上时，请直接写出点G的坐标

查看试题解析

x(h)	…	11	12	13	14	15	16	17	18	…
y(cm)	…	189	137	103	80	101	133	202	260	…