北京市房山区2023年中考二模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列几何体的主视图和俯视图完全相同的是( )A、
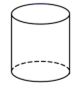 B、
B、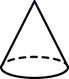 C、
C、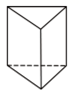 D、
D、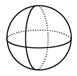 2. 2022年我国的进出口总额超过了6万亿美元,实际使用外资亿美元,规模再创历史新高.将189130000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,用量角器测量 , 可读出的度数为( )
2. 2022年我国的进出口总额超过了6万亿美元,实际使用外资亿美元,规模再创历史新高.将189130000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,用量角器测量 , 可读出的度数为( ) A、 B、 C、 D、4. 实数 , 在数轴上的对应点的位置如图所示,表示实数的点在原点右侧,且 , 下列结论中正确的是( )
A、 B、 C、 D、4. 实数 , 在数轴上的对应点的位置如图所示,表示实数的点在原点右侧,且 , 下列结论中正确的是( ) A、 B、 C、 D、5. 下列图形中,点是该图形的对称中心的是( )A、
A、 B、 C、 D、5. 下列图形中,点是该图形的对称中心的是( )A、 B、
B、
C、 D、
D、 6. 不透明的盒子中有三张卡片,上面分别写有数字“ , , ”,除数字外三张卡片无其他差别从中随机取出一张卡片,记录其数字,放回并摇匀,再从中随机取出一张卡片,记录其数字,两次取出卡片上的数字的乘积是偶数的概率是( )A、 B、 C、 D、7. 已知 , , , 若为整数,且 , 则的值是( )A、 B、 C、 D、8. 如图 , 在中, , , , 分别是边 , 的中点,点为线段上的一个动点,连接 , , 设 , 图中某条线段长为 , 若表示与的函数关系的图象大致如图所示,则这条线段可能是( )
6. 不透明的盒子中有三张卡片,上面分别写有数字“ , , ”,除数字外三张卡片无其他差别从中随机取出一张卡片,记录其数字,放回并摇匀,再从中随机取出一张卡片,记录其数字,两次取出卡片上的数字的乘积是偶数的概率是( )A、 B、 C、 D、7. 已知 , , , 若为整数,且 , 则的值是( )A、 B、 C、 D、8. 如图 , 在中, , , , 分别是边 , 的中点,点为线段上的一个动点,连接 , , 设 , 图中某条线段长为 , 若表示与的函数关系的图象大致如图所示,则这条线段可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共16.0分)
-
9. 若代数式在实数范围内有意义,则实数的取值范围是 .10. 分解因式: .11. 方程的解为 .12. 在平面直角坐标系中,若反比例函数的图象经过点和点 , 则的值为 .13. 若关于的一元二次方程有两个实数根,则实数的取值范围是 .14. 如图,点 , , 在上,若 , , 则的半径为 .
 15. 某公司销售部在出售一批柑橘前需要先进行“柑橘损坏率”统计,去掉损坏的柑橘后,再确定柑橘的售价表是销售部随机取样得到的“柑橘损坏率”统计表的一部分:
15. 某公司销售部在出售一批柑橘前需要先进行“柑橘损坏率”统计,去掉损坏的柑橘后,再确定柑橘的售价表是销售部随机取样得到的“柑橘损坏率”统计表的一部分:柑橘总质量
损坏的柑橘质量
柑橘损坏的频率
估计这批柑橘完好的概率为 结果精确到 .
16. 甲、乙、丙三位同学进行象棋比赛训练,两人先比,若分出胜负,则由第三个人与胜者比赛;若是和棋,则这两个人继续下一局比赛,直到分出胜负如此进行比赛若干局后,甲胜局,负局;乙胜局,负局;若丙负局,那么丙胜了 局,三位同学至少进行了 局比赛.三、解答题(本大题共12小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 解不等式组:19. 已知 , 求代数式的值.20. 下面是晓彤在证明“平行四边形的对角相等”这个性质定理时使用的三种添加辅助线的方法,请你选择其中一种,完成证明.
平行四边形性质定理:平行四边形的对角相等.

已知:如图, .
求证: , .
方法一:
证明:如图,连接AC .

方法二:
证明:如图,延长BC至点E .

方法三:
证明:如图,连接AC、BD,AC与BD交于点O .
 21. 如图,点为▱的对角线的中点,直线绕点旋转,当时,与边 , 分别交于点 , , 连接 , .
21. 如图,点为▱的对角线的中点,直线绕点旋转,当时,与边 , 分别交于点 , , 连接 , .
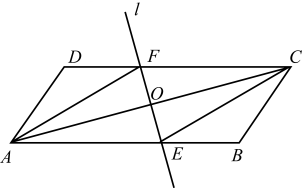 (1)、求证:四边形是菱形;(2)、若 , , , 求▱的面积.22. 在平面直角坐标系中,函数的图象经过点 , 且与函数的图象交于点 .(1)、求的值及函数的表达式;(2)、当时,对于的每一个值,函数的值小于函数的值,直接写出的取值范围.23. 如图, , , 三点在上,直径平分 , 过点作交弦于点 , 在的延长线上取一点 , 使得 .
(1)、求证:四边形是菱形;(2)、若 , , , 求▱的面积.22. 在平面直角坐标系中,函数的图象经过点 , 且与函数的图象交于点 .(1)、求的值及函数的表达式;(2)、当时,对于的每一个值,函数的值小于函数的值,直接写出的取值范围.23. 如图, , , 三点在上,直径平分 , 过点作交弦于点 , 在的延长线上取一点 , 使得 .
 (1)、求证:是的切线;(2)、若 , , 求的长.24. 青少年的健康素质是全民族健康素质的基础某校为了解学生寒假参加体育锻炼的
(1)、求证:是的切线;(2)、若 , , 求的长.24. 青少年的健康素质是全民族健康素质的基础某校为了解学生寒假参加体育锻炼的
情况,从七、八、九年级学生中各随机抽取了该年级学生人数的 , 调查了他们平均每周参加体育锻炼的时长,并对这些数据进行整理、描述和分析,下面给出部分信息.
七,八年级学生平均每周参加体育锻炼时长数据的折线图如下:
九年级学生平均每周参加体育锻炼的时长:
, , , , , , , ;
七、八、九年级学生平均每周参加体育锻炼时长的平均数、中位数、众数:年级
平均数
中位数
众数
七年级
,
八年级
九年级
根据所给信息,回答下列问题:
(1)、表中的值是 ,的值是 ,的值是 ;(2)、设七、八、九三个年级学生参加体育锻炼时长的方差分别是 , , , 直接写出 , , 之间的大小关系用“”连接;(3)、估计全校九年级所有学生中,共有 名学生参加体育锻炼的时长不少于小时.25. 排球场的长度为 , 球网在场地中央且高度为排球出手后的运动路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,排球运动过程中的竖直高度单位:与水平距离单位:近似满足函数关系 . (1)、某运动员第一次发球时,测得水平距离与竖直高度的几组数据如下:
(1)、某运动员第一次发球时,测得水平距离与竖直高度的几组数据如下:水平距离
竖直高度
根据上述数据,求这些数据满足的函数关系;
判断该运动员第一次发球能否过网 ▲ 填“能”或“不能” .(2)、该运动员第二次发球时,排球运动过程中的竖直高度单位:与水平距离单位:近似满足函数关系 , 请问该运动员此次发球是否出界,并说明理由.26. 平面直角坐标系中,抛物线的对称轴为直线 .(1)、若抛物线经过点 , 求和的值;(2)、若抛物线上存在两点和 , .
判断抛物线的开口方向;并说明理由;
若 , 求的取值范围.27. 如图, , , 点是延长线上一点,连接 , 点和点关于直线对称,连接交于点 , 连接 , , . (1)、依题意补全图形,并求的度数;(2)、用等式表示线段 , 和之间的数量关系,并证明.28. 在平面直角坐标系中,有图形和点 , 我们规定:若图形上存在点、点和可以重合 , 满足 , 其中点是点关于轴的对称点,则称点是图形的“对称平衡点”.
(1)、依题意补全图形,并求的度数;(2)、用等式表示线段 , 和之间的数量关系,并证明.28. 在平面直角坐标系中,有图形和点 , 我们规定:若图形上存在点、点和可以重合 , 满足 , 其中点是点关于轴的对称点,则称点是图形的“对称平衡点”. (1)、如图所示,已知,点 , 点 .
(1)、如图所示,已知,点 , 点 .
在点 , , 中,是线段的“对称平衡点”的是 ▲ ;
线段上是否存在线段的“对称平衡点”?若存在,请求出符合要求的“对称平衡点”的横坐标的范围,若不存在,请说明理由.(2)、如图 , 以点为圆心,为半径作坐标系内的点满足 , 再以点为圆心,为半径作 , 若上存在的“对称平衡点”,直接写出点纵坐标的取值范围.