北京市海淀区2023年中考二模数学考试试卷

试卷更新日期：2023-09-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，共16.0分。在每小题列出的选项中，选出符合题目的一项）

1. 一个正五棱柱如右图摆放，光线由上到下照射此正五棱柱时的正投影是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $2 a + 3 a = 5 a^{2}$ B、 $a \cdot a \cdot a = 3 a$
C、 $(a^{3})^{2} = a^{5}$ D、 $a (m + n) = a m + a n$

查看试题解析
3. 实数 $a$ 在数轴上对应点的位置如图所示 $.$ 若实数 $b$ 满足 $a + b < 0$ ，则 $b$ 的值可以是（）

A、 $- 2$ B、 $- 1$ C、 $0$ D、 $1$

查看试题解析
4. 如图，由正六边形和正三角形组成的图形为轴对称图形，该图形的对称轴的条数为（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
5. 投掷两枚质地均匀的骰子，两枚骰子向上一面的点数相同的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 如果 $a - b = 2$ ，那么代数式 $\frac{2}{a + b} \cdot (1 + \frac{2 b}{a - b})$ 的值是（）

A、 $\frac{1}{2}$ B、 $1$ C、 $\sqrt{2}$ D、 $2$

查看试题解析
7. 如图，在正方形网格中，以点 $O$ 为位似中心， $△ A B C$ 的位似图形可以是（）

A、 $△ D E F$ B、 $△ D H F$ C、 $△ G E H$ D、 $△ G D H$

查看试题解析

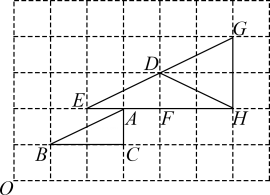8. 小明近期计划阅读一本总页数不低于

300

页的名著，他制定的阅读计划如下：

星期	一	二	三	四	五	六	日
页数	$15$	$20$	$15$	$10$	$20$	$40$	$30$

若小明按照计划从星期 $x$ 开始连续阅读， $10$ 天后剩下的页数为 $y$ ，则 $y$ 与 $x$ 的图象可能为（）

A、

B、

C、

D、

查看试题解析

二、填空题（本大题共8小题，共16.0分）

9. 若代数式 $\frac{1}{2 - x}$ 有意义，则实数 $x$ 的取值范围是．

查看试题解析
10. 分解因式： $a x^{2} - 4 a =$ .

查看试题解析
11. 用一个 $x$ 的值说明“ $\sqrt{x^{2}} = x$ ”是错误的，则 $x$ 的值可以是．

查看试题解析
12. 如图，正方形 $A B C D$ ，点 $A$ 在直线 $l$ 上，点 $B$ 到直线 $l$ 的距离为 $3$ ，点 $D$ 到直线 $l$ 的距离为 $2$ ，则正方形的边长为．

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，点 $A (1 ， y_{1})$ 和点 $B (3 ， y_{2})$ 在反比例函数 $y = \frac{k}{x}$ 的图象上 $.$ 若 $y_{1} < y_{2}$ ，写出一个满足条件的 $k$ 的值．

查看试题解析

14. 咖啡树种子的发芽能力会随着保存时间的增长而减弱，咖啡树种子保存到三个月时，发芽率约为

95 %

；从三个月到五个月，发芽率会逐渐降到

75 %

；从五个月到九个月，发芽率会逐渐降到

25 % .

农科院记录了某批咖啡树种子的发芽情况，结果如下表所示：

种子数量 $n$	$10$	$50$	$150$	$300$	$500$	$800$
发芽数量 $m$	$9$	$41$	$133$	$261$	$431$	$689$
发芽率 $\frac{m}{n}$	$0.9$	$0.82$	$0.887$	$0.87$	$0.862$	$0.861$

据此推测，下面三个时间段中，这批咖啡树种子的保存时间是 $($ 填“三个月内”“三至五个月”或“五至九个月” $)$ ．

查看试题解析

15. 如图， $A B$ 为 $⊙ O$ 的弦， $C$ 为 $⊙ O$ 上一点， $O C ⊥ A B$ 于点 $D .$ 若 $O A = \sqrt{10}$ ， $A B = 6$ ，则 $t a n ∠ A O D =$ ．

查看试题解析
16. 四个互不相等的实数 $a$ ， $b$ ， $c$ ， $m$ 在数轴上的对应点分别为 $A$ ， $B$ ， $C$ ， $M$ ，其中 $a = 4$ ， $b = 7$ ， $c$ 为整数， $m = 0.2 (a + b + c)$ ．

(1)、若 $c = 10$ ，则 $A$ ， $B$ ， $C$ 中与 $M$ 距离最小的点为；

(2)、若在 $A$ ， $B$ ， $C$ 中，点 $C$ 与点 $M$ 的距离最小，则符合条件的点 $C$ 有个 $.$

查看试题解析

三、解答题（本大题共12小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

17. 计算： $(\frac{1}{2})^{- 1} + | 1 - \sqrt{3} | - t a n 60 ° - (π + 2023)^{0}$ ．

查看试题解析
18. 解不等式 $\frac{x - 1}{2} \geq \frac{2}{3} x - 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、使用直尺和圆规，作 $A D ⊥ B C$ 交 $B C$ 于点 $D ($ 保留作图痕迹 $)$ ；

(2)、以 $D$ 为圆心， $D C$ 的长为半径作弧，交 $A C$ 于点 $E$ ，连接 $B E$ ， $D E$ ．
$① ∠ B E C =$ $°$ ；
$②$ 写出图中一个与 $∠ C B E$ 相等的角．

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0 (m < 0)$ ．

(1)、判断方程根的情况，并说明理由；

(2)、若方程的一个根为 $- 1$ ，求 $m$ 的值和方程的另一个根．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，直线 $y = k x - 1$ 与 $y = \frac{1}{2} x$ 交于点 $A (2 ， m)$ ．

(1)、求 $k$ ， $m$ 的值；

(2)、已知点 $P (n ， 0)$ ，过点 $P$ 作垂直于 $x$ 轴的直线交直线 $y = k x - 1$ 于点 $M$ ，交直线 $y = \frac{1}{2} x$ 于点 $N .$ 若 $M N = 2$ ，直接写出 $n$ 的值．

查看试题解析
22. 如图，平行四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $O$ ， $E$ 为 $O A$ 的中点 $.$ 连接 $D E$ 并延长至点 $F$ ，使得 $E F = D E .$ 连接 $A F$ ， $B F$ ．

(1)、求证：四边形 $A F B O$ 为平行四边形；

(2)、若 $∠ B D A = ∠ B D C$ ，求证：四边形 $A F B O$ 为矩形．

查看试题解析

23. 某企业生产甲、乙两款红茶，为了解两款红茶的质量，请消费者和专业机构分别测评

.

随机抽取

25

名消费者对两款红茶评分，并对数据进行整理、描述和分析，下面给出了部分信息．

a .

甲款红茶分数

(

百分制

)

的频数分布表如下：

分数	$70 \leq x < 75$	$75 \leq x < 80$	$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x \leq 100$
频数	$2$	$1$	$4$			$4$

$b .$ 甲款红茶分数在 $85 \leq x < 90$ 这一组的是：
$86 86 86 86 86 87 87 88 88 89$
$c .$ 甲、乙两款红茶分数的平均数、众数、中位数如下表所示：

品种	平均数	众数	中位数
甲	$86.6$	$m$	$n$
乙	$87.5$	$90$	$86$

根据以上信息，回答下列问题：

(1)、补全甲款红茶分数的频数分布直方图；

(2)、表格中

m

的值为，

n

的值为；

(3)、专业机构对两款红茶的条索、色泽、整碎、净度、内质、香气、滋味醇厚度、汤色、叶底来进行综合评分如下：甲款红茶

93

分，乙款红茶

87

分，若以这

25

名消费者评分的平均数和专业机构的评分按照

6

：

4

的比例确定最终成绩，可以认定款红茶最终成绩更高

(

填“甲”或“乙”

)

．

查看试题解析

24. 如图， $P$ 为 $⊙ O$ 外一点， $P A$ ， $P B$ 是 $⊙ O$ 的切线， $A$ ， $B$ 为切点，点 $C$ 在 $⊙ O$ 上，连接 $O A$ ， $O C$ ， $A C$ ．

(1)、求证： $∠ A O C = 2 ∠ P A C$ ；

(2)、连接 $O B$ ，若 $A C / / O B$ ， $⊙ O$ 的半径为 $5$ ， $A C = 6$ ，求 $A P$ 的长．

查看试题解析

25. 小明发现某乒乓球发球器有“直发式”与“间发式”两种模式，在“直发式”模式下，球从发球器出口到第一次接触台面的运动轨迹近似为一条抛物线；在“间发式”模式下，球从发球器出口到第一次接触台面的运动轨迹近似为一条直线，球第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线

.

如图

1

和图

2

分别建立平面直角坐标系

x O y

．

通过测量得到球距离台面高度 $y ($ 单位： $d m)$ 与球距离发球器出口的水平距离 $x ($ 单位： $d m)$ 的相关数据，如下表所示：
表 $1$ 直发式

$x (d m)$	$0$	$2$	$4$	$6$	$8$	$10$	$16$	$20$	$\dots$
$y (d m)$	$3.84$	$3.96$	$4$	$3.96$	$m$	$3.64$	$2.56$	$1.44$	$\dots$

表 $2$ 间发式

$x (d m)$	$0$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	$16$	$18$	$\dots$
$y (d m)$	$3.36$	$n$	$1.68$	$0.84$	$0$	$1.40$	$2.40$	$3$	$3.20$	$3$	$\dots$

根据以上信息，回答问题：

(1)、表格中

m =

，

n =

；

(2)、求“直发式”模式下，球第一次接触台面前的运动轨迹的解析式；

(3)、若“直发式”模式下球第一次接触台面时距离出球点的水平距离为

d_{1}

， “间发式”模式下球第二次接触台面时距离出球点的水平距离为

d_{2}

，则

d_{1}

d_{2} (

填“

>

”“

=

”或“

<

”

)

．

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} + b x + a + 2 (a > 0)$ 过点 $(1 ， 4 a + 2)$ ．

(1)、求该抛物线的顶点坐标；

(2)、过该抛物线与 $y$ 轴的交点作 $y$ 轴的垂线 $l$ ，将抛物线在 $y$ 轴右侧的部分沿直线 $l$ 翻折，其余部分保持不变，得到图形 $G$ ， $M (- 1 - a ， y_{1})$ ， $N (- 1 + a ， y_{2})$ 是图形 $G$ 上的点，设 $t = y_{1} + y_{2}$ ．
$①$ 当 $a = 1$ 时，求 $t$ 的值；
$②$ 若 $6 \leq t \leq 9$ ，求 $a$ 的取值范围．

查看试题解析
27. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 2 α (45 ° < α < 90 °) D$ 是 $B C$ 的中点， $E$ 是 $B D$ 的中点，连接 $A E .$ 将射线 $A E$ 绕点 $A$ 逆时针旋转 $α$ 得到射线 $A M$ ，过点 $E$ 作 $E F ⊥ A E$ 交射线 $A M$ 于点 $F$ ．

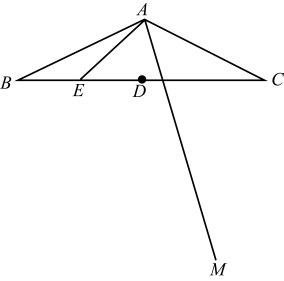(1)、 $①$ 依题意补全图形；
$②$ 求证： $∠ B = ∠ A F E$ ；

(2)、连接 $C F$ ， $D F$ ，用等式表示线段 $C F$ ， $D F$ 之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于 $△ O A B$ 和点 $P ($ 不与点 $O$ 重合 $)$ 给出如下定义：若边 $O A$ ， $O B$ 上分别存在点 $M$ ，点 $N$ ，使得点 $O$ 与点 $P$ 关于直线 $M N$ 对称，则称点 $P$ 为 $△ O A B$ 的“翻折点”．

(1)、已知 $A (3 ， 0)$ ， $B (0 ， 3 \sqrt{3}) .$
$①$ 若点 $M$ 与点 $A$ 重合，点 $N$ 与点 $B$ 重合，直接写出 $△ O A B$ 的“翻折点”的坐标；
$② P$ 是线段 $A B$ 上一动点，当 $P$ 是 $△ O A B$ 的“翻折点”时，求 $A P$ 长的取值范围；

(2)、直线 $y = - \frac{3}{4} x + b (b > 0)$ 与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点，若存在以直线 $A B$ 为对称轴，且斜边长为 $2$ 的等腰直角三角形，使得该三角形边上任意一点都为 $△ O A B$ 的“翻折点”，直接写出 $b$ 的取值范围．

查看试题解析