天津市南开区2023年中考二模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算的结果是( )A、 B、 C、 D、2. 下列三角函数中,结果为的是( )A、 B、 C、 D、3. 下列绿色能源图标中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 将数字用科学记数法可表示为( )A、 B、 C、 D、5. 如图是由若干个小正方体堆成的几何体的主视图(正视图),这个几何体是( )
4. 将数字用科学记数法可表示为( )A、 B、 C、 D、5. 如图是由若干个小正方体堆成的几何体的主视图(正视图),这个几何体是( )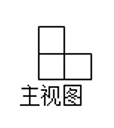 A、
A、 B、
B、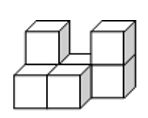 C、
C、 D、
D、 6. 估计的值在( )A、和之间 B、和之间 C、和之间 D、和之间7. 化简的结果为( )A、 B、 C、 D、8. 点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 方程的两根为 , , 下列表示根与系数关系的等式中,正确的是( )A、 , B、
6. 估计的值在( )A、和之间 B、和之间 C、和之间 D、和之间7. 化简的结果为( )A、 B、 C、 D、8. 点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 方程的两根为 , , 下列表示根与系数关系的等式中,正确的是( )A、 , B、
C、 D、10. 如图,▱的顶点坐标分别为、、 , 则点的坐标为( ) A、
A、
B、
C、
D、11. 对折矩形 , 使和重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点落在上的点处,并使折痕经过点 , 得到折痕 , 同时得到线段则下列结论错误的是( ) A、 B、 C、 D、12. 如图所示是抛物线的部分图象,其顶点坐标为 , 且与轴的一个交点在点和之间,则下列结论:;;;一元二次方程没有实数根其中正确的结论个数是( )
A、 B、 C、 D、12. 如图所示是抛物线的部分图象,其顶点坐标为 , 且与轴的一个交点在点和之间,则下列结论:;;;一元二次方程没有实数根其中正确的结论个数是( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本大题共6小题,共18.0分)
-
13. 计算 .14. 计算:的结果等于 .15. 有张背面完全相同的卡片,正面分别标有 , , , , , , 把这张卡片背面朝上,随机抽取其中的一张,卡片上的数是负数的概率为 .16. 直线与轴交于正半轴,则的值可以是 .17. 如图,在平行四边形中,对角线、相交于点 , , 点 , 点分别是 , 的中点,连接 , , 于点 , 交于点 , , 则线段的长为 .
 18. 如图,在每个小正方形的边长为的网格中,圆上的点 , , 及点均在格点上.
18. 如图,在每个小正方形的边长为的网格中,圆上的点 , , 及点均在格点上. (1)、的大小为 度;(2)、为上一点,连接 , 将绕点顺时针旋转得到请用无刻度的直尺,在如图所示的网格中,画出线段 , 并简要说明点 , 的位置是如何找到的不要求证明 .
(1)、的大小为 度;(2)、为上一点,连接 , 将绕点顺时针旋转得到请用无刻度的直尺,在如图所示的网格中,画出线段 , 并简要说明点 , 的位置是如何找到的不要求证明 .三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 解不等式组 , 请按下列步骤完成解答:
⑴解不等式 , 得 ▲ ;
⑵解不等式 , 得 ▲ ;
⑶把不等式和的解集在数轴上表示出来;
⑷原不等式组的解集为 ▲ .
20. 某校为了解八年级学生参加社会实践活动情况,随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题: (1)、本次接受随机抽样调查的学生人数为 , 图①中的m的值为;(2)、求本次抽样调查获取的样本数据的众数、中位数和平均数;(3)、若该校八年级学生有1200人,估计参加社会实践活动时间大于7天的学生人数.21. 已知中,直径长为 , 、分别切于点 , , 弦 .
(1)、本次接受随机抽样调查的学生人数为 , 图①中的m的值为;(2)、求本次抽样调查获取的样本数据的众数、中位数和平均数;(3)、若该校八年级学生有1200人,估计参加社会实践活动时间大于7天的学生人数.21. 已知中,直径长为 , 、分别切于点 , , 弦 . (1)、如图 , 若 , 求的大小和弦的长;(2)、如图 , 过点的切线分别与、的延长线交于点 , , 且 , 求弦的长.22. 如图,为测量一段笔直自西向东的河流的河面宽度,小明在河北岸处测得对岸处一棵树位于南偏西方向,处一棵树位于南偏东方向,已知两树、相距 , 求此段河面的宽度结果取整数,参考数据: , , , , ,
(1)、如图 , 若 , 求的大小和弦的长;(2)、如图 , 过点的切线分别与、的延长线交于点 , , 且 , 求弦的长.22. 如图,为测量一段笔直自西向东的河流的河面宽度,小明在河北岸处测得对岸处一棵树位于南偏西方向,处一棵树位于南偏东方向,已知两树、相距 , 求此段河面的宽度结果取整数,参考数据: , , , , , 23. 某实验室对甲、乙两机器人进行装卸货物测试,在实验场地的一条直线上依次设置货物装卸点 , , 三地,甲、乙两机器人同时从地匀速出发,甲机器人到达地后装货分钟,再以原速原路返回地,乙机器人到达地后装货分钟,再以原速前往地,结果甲、乙两机器人同时到达各自目的地,在两机器人行驶的过程中,甲、乙两机器人距地的距离单位:米与甲机器人所用时间单位:分之间的函数图象如图所示:请结合图象信息解答下列问题:
23. 某实验室对甲、乙两机器人进行装卸货物测试,在实验场地的一条直线上依次设置货物装卸点 , , 三地,甲、乙两机器人同时从地匀速出发,甲机器人到达地后装货分钟,再以原速原路返回地,乙机器人到达地后装货分钟,再以原速前往地,结果甲、乙两机器人同时到达各自目的地,在两机器人行驶的过程中,甲、乙两机器人距地的距离单位:米与甲机器人所用时间单位:分之间的函数图象如图所示:请结合图象信息解答下列问题:
(1)、填空:
、两地之间的距离为 米;
甲机器人从出发到返回地,共用时 分钟;
甲机器人的速度为 米分;
乙机器人的速度为 米分;
两机器人在第 分时相距米;(2)、写出乙机器人行驶的全过程中与的函数关系式.24. 四边形在平面直角坐标系中,已知点 , 、两点分别在轴、轴正半轴上,且 .
 (1)、如图 , 求点和点的坐标;(2)、如图 , 点为线段上一点不包括、 , 把线段绕点顺时针旋转得到线段 .
(1)、如图 , 求点和点的坐标;(2)、如图 , 点为线段上一点不包括、 , 把线段绕点顺时针旋转得到线段 .
连接 , 设点的横坐标为 , 的面积为 , 求与的函数关系式,并直接写出自变量的取值范围;
如图 , 连接 , 点在的延长线上,且 , 若点的横坐标等于 , 请直接写出四边形的面积以及点的坐标.25. 已知抛物线是常数的开口向上且经过点 , .(1)、当时,求抛物线的顶点坐标;(2)、若二次函数在时,的最大值为 , 求的值;(3)、若射线与抛物线仅有一个公共点,求的取值范围.