天津市东丽区2023年中考一模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算的值是( )A、 B、 C、 D、2. 的值等于()A、 B、 C、1 D、3. 天津水滴体育馆占地平方米,数字用科学记数法表示应为( )A、 B、 C、 D、4. 在一些美术字中,有的汉字是轴对称的下面个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图是一个由个相同的正方体组成的立体图形,它的俯视图是( )
5. 如图是一个由个相同的正方体组成的立体图形,它的俯视图是( ) A、
A、 B、
B、 C、
C、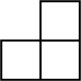 D、
D、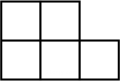 6. 估计的值在( )A、和之间 B、和之间 C、和之间 D、和之间7. 计算的结果是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,四边形为菱形, , , , 则对角线交点的坐标为( )
6. 估计的值在( )A、和之间 B、和之间 C、和之间 D、和之间7. 计算的结果是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,四边形为菱形, , , , 则对角线交点的坐标为( ) A、 B、 C、 D、9. 方程组 的解是( )A、 B、 C、 D、10. 若点 , , 都在反比例函数的图象上,若则 , , 的大小关系是( )A、 B、 C、 D、11. 如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为 , 则下列结论一定正确的是( )
A、 B、 C、 D、9. 方程组 的解是( )A、 B、 C、 D、10. 若点 , , 都在反比例函数的图象上,若则 , , 的大小关系是( )A、 B、 C、 D、11. 如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为 , 则下列结论一定正确的是( ) A、 B、AB+CE=BC C、DE+DC=AB D、12. 已知二次函数是常数,图象的对称轴是直线 , 经过点 , , 且 , , 现有下列结论:;;; , 其中正确结论的个数是( )A、 B、 C、 D、
A、 B、AB+CE=BC C、DE+DC=AB D、12. 已知二次函数是常数,图象的对称轴是直线 , 经过点 , , 且 , , 现有下列结论:;;; , 其中正确结论的个数是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
13. 计算的结果等于 .14. 计算的结果等于 .15. 把一副普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的牌是黑桃4的概率是.
 16. 把直线向下平移个单位长度,平移后的直线解析式为 .17. 如图,正方形的边长为 , 点是边中点,垂直平分且分别交、于点、 , 则的长为 .
16. 把直线向下平移个单位长度,平移后的直线解析式为 .17. 如图,正方形的边长为 , 点是边中点,垂直平分且分别交、于点、 , 则的长为 . 18. 如图,在网格中,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,点 , , 均为格点,点 , , 均在以格点为圆心的圆上.
18. 如图,在网格中,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,点 , , 均为格点,点 , , 均在以格点为圆心的圆上. (1)、线段的长等于 .(2)、请你只用无刻度的直尺,在线段上画点 , 使 , 并简要说明点是如何找到的不要求证明 .
(1)、线段的长等于 .(2)、请你只用无刻度的直尺,在线段上画点 , 使 , 并简要说明点是如何找到的不要求证明 .三、解答题(本大题共7小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 解不等式组.
请结合题意填空,完成本题的解答.
⑴ 解不等式 , 得 ▲ ;⑵解不等式 , 得 ▲ ;
⑶把不等式和的解集在数轴上分别表示出来;
⑷原不等式组的解集为 ▲ .
20. 某校名学生参加植树活动,要求每人植树的范围是棵棵,活动结束后随机抽查了若干名学生每人的植树量,并绘制成如下统计图.
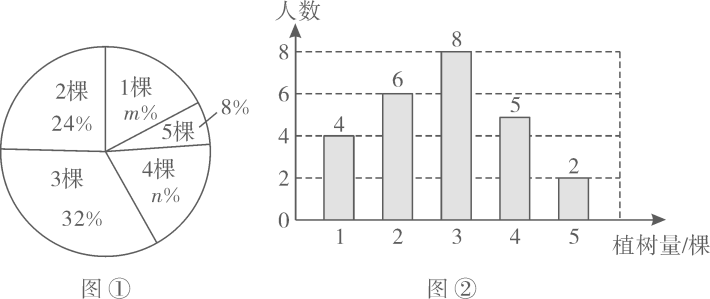
请根据相关信息,解答下列问题:(1)、扇形统计图中的 ; ;(2)、求被调查学生每人植树量的众数、中位数;(3)、估计该校名学生在这次植树活动中共植树多少棵.21. 如图,四边形内接于 , 为的直径, . (1)、求的度数;(2)、若 , , 求的长度.22. 如图,建筑物上有一旗杆 , 从处观测旗杆顶部的仰角为 , 观测旗杆底部的仰角为 , 已知旗杆的高度为 , 求建筑物的高度结果精确到米,参考数据: , ,
(1)、求的度数;(2)、若 , , 求的长度.22. 如图,建筑物上有一旗杆 , 从处观测旗杆顶部的仰角为 , 观测旗杆底部的仰角为 , 已知旗杆的高度为 , 求建筑物的高度结果精确到米,参考数据: , , 23. 已知 , 两地相距 , 甲、乙两人沿同一条公路从地出发到地,甲骑自行车匀速行驶到达,乙骑摩托车,比甲迟出发,行至处追上甲,停留后继续以原速行驶他们离开地的路程单位:与行驶时间单位:之间的关系如图所示.
23. 已知 , 两地相距 , 甲、乙两人沿同一条公路从地出发到地,甲骑自行车匀速行驶到达,乙骑摩托车,比甲迟出发,行至处追上甲,停留后继续以原速行驶他们离开地的路程单位:与行驶时间单位:之间的关系如图所示. (1)、根据题意填空:甲行驶的速度为 , 乙行驶的速度为 ;(2)、当时,直接写出乙离开地的路程与之间的函数关系式;(3)、当乙再次追上甲时距离地 .
(1)、根据题意填空:甲行驶的速度为 , 乙行驶的速度为 ;(2)、当时,直接写出乙离开地的路程与之间的函数关系式;(3)、当乙再次追上甲时距离地 .
