天津市红桥区2023年中考一模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算的结果等于( )A、 B、 C、 D、2. 的值等于( )A、 B、 C、 D、3. 下列图案中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 将用科学记数法表示应为( )A、 B、 C、 D、5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
4. 将用科学记数法表示应为( )A、 B、 C、 D、5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、 C、
C、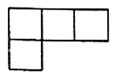 D、
D、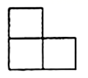 6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 方程组的解是( )A、 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 计算的结果是( )A、 B、 C、 D、10. 如图,四边形是矩形,A , B两点的坐标分别是 , , 点C在第一象限,则点C的坐标为( )
6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 方程组的解是( )A、 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 计算的结果是( )A、 B、 C、 D、10. 如图,四边形是矩形,A , B两点的坐标分别是 , , 点C在第一象限,则点C的坐标为( )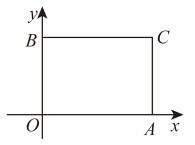 A、 B、 C、 D、11. 如图,在中, , 将绕点顺时针旋转得到 , 点 , 的对应点分别为 , 当的延长线经过点时,则下列结论一定正确的是( )
A、 B、 C、 D、11. 如图,在中, , 将绕点顺时针旋转得到 , 点 , 的对应点分别为 , 当的延长线经过点时,则下列结论一定正确的是( )
 A、 B、 C、 D、12. 开口向下的抛物线为常数,与轴的负半轴交于点 , 对称轴为直线有下列结论:;函数的最大值为;若关于的方程无实数根,则其中,正确结论的个数是( )A、 B、 C、 D、
A、 B、 C、 D、12. 开口向下的抛物线为常数,与轴的负半轴交于点 , 对称轴为直线有下列结论:;函数的最大值为;若关于的方程无实数根,则其中,正确结论的个数是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
13. 计算的结果等于 .14. 计算的结果等于 .15. 不透明袋子中装有个球,其中有个红球和个蓝球,这些球除颜色外无其他差别从袋子中随机取出个球,则它是蓝球的概率是 .16. 若一次函数是常数的图象经过第一、二、三象限,则的取值范围是 .17. 如图,已知正方形的边长为 , 为的中点,为上一点,且 , 若 , 分别为 , 的中点,连接 , 则的长为 .
 18. 如图,在每个小正方形的边长为的网格中,的顶点 , , 均在格点上,是的内切圆.
18. 如图,在每个小正方形的边长为的网格中,的顶点 , , 均在格点上,是的内切圆. (1)、线段的长等于 ;
(1)、线段的长等于 ;
(2)、的半径的长等于 ;
(3)、是上的动点,当取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 , 并简要说明点的位置是如何找到的不要求证明 .三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 解不等式组
请结合题意填空,完成本题的解答.⑴解不等式 , 得 ▲ ;
⑵解不等式 , 得 ▲ ;
⑶把不等式和的解集在数轴上表示出来:

⑷原不等式组的解集为 ▲ .20. 某校在一次体育测试中,随机抽取了部分男生每人完成引体向上的次数根据统计的结果,绘制出如下的统计图和图 .
请根据相关信息,解答下列问题:
(1)、本次接受随机抽样调查的男生人数为 ,图中的值为 ;(2)、求统计的这组次数数据的平均数、众数和中位数.21. 在中,为直径,过上一点作的切线,与的延长线交于点 , 连接 . (1)、如图 , 若 , 求的大小;(2)、如图 , 过点作的垂线,垂足为 , 交于点 , 连接 , 若 , , 求的长.22. 小琪要测量某建筑物的高度如图,小琪在点处测得该建筑物的最高点的仰角为 , 再往该建筑物方向前进至点处测得最高点的仰角为根据测得的数据,计算该建筑物的高度结果取整数 . 参考数据: , , .
(1)、如图 , 若 , 求的大小;(2)、如图 , 过点作的垂线,垂足为 , 交于点 , 连接 , 若 , , 求的长.22. 小琪要测量某建筑物的高度如图,小琪在点处测得该建筑物的最高点的仰角为 , 再往该建筑物方向前进至点处测得最高点的仰角为根据测得的数据,计算该建筑物的高度结果取整数 . 参考数据: , , . 23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.

已知小明家、体育馆、图书馆依次在同一条直线上小明从家出发,匀速骑行到达体育馆;在体育馆停留一段时间后,匀速步行到达图书馆;在图书馆停留一段时间后,匀速骑行返回家中,给出的图象反映了这个过程中小明离开家的距离与离开家的时间之间的对应关系.
请根据相关信息,解答下列问题:(1)、填表:小明离开家的时间
小明离开家的距离
▲
▲
▲
(2)、填空:
体育馆与图书馆之间的距离为 ▲ ;
小明从体育馆到图书馆的步行速度为 ▲ ;
当小明离开家的距离为时,他离开家的时间为 ▲
(3)、当时,请直接写出关于的函数解析式.24. 将一个矩形纸片放置在平面直角坐标系中,点 , 点 , 点 , 点在边上点不与点 , 重合 , 折叠该纸片,使折痕所在的直线经过点 , 并与轴的正半轴相交于点 , 且 , 点的对应点落在第一象限设 . (1)、如图 , 当时,求的大小和点的坐标;(2)、如图 , 若折叠后重合部分为四边形,点的对应点为 , 且在直线的下方, , 分别与边相交于点 , , 试用含有的式子表示重合部分的面积 , 并直接写出的取值范围;(3)、若折叠后重合部分的面积为 , 求的值直接写出结果即可 .
(1)、如图 , 当时,求的大小和点的坐标;(2)、如图 , 若折叠后重合部分为四边形,点的对应点为 , 且在直线的下方, , 分别与边相交于点 , , 试用含有的式子表示重合部分的面积 , 并直接写出的取值范围;(3)、若折叠后重合部分的面积为 , 求的值直接写出结果即可 .
25. 抛物线为常数,交轴于 , 两点.(1)、求该抛物线的解析式;(2)、点 , 是线段上的动点点不与点 , 重合 .
点关于轴的对称点为 , 当点在该抛物线上时,求点的坐标;
是线段上的动点点不与点 , 重合 , 且 , 连接 , , 当取得最小值时,求点的坐标.