重庆市两江新区2023年中考一模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 下列图案是中心对称图形的是( )A、
 B、
B、
C、 D、
D、 3. 下列各式中,是多项式的是( )A、 B、 C、 D、4. 油箱中存油升,油从油箱中均匀流出,流速为升分钟,则油箱中剩余油量升与流出时间分钟的函数关系是( )A、 B、 C、 D、5. 如图,与是位似图形,点是位似中心,若:: , 的面积为 , 则的面积为( )
3. 下列各式中,是多项式的是( )A、 B、 C、 D、4. 油箱中存油升,油从油箱中均匀流出,流速为升分钟,则油箱中剩余油量升与流出时间分钟的函数关系是( )A、 B、 C、 D、5. 如图,与是位似图形,点是位似中心,若:: , 的面积为 , 则的面积为( )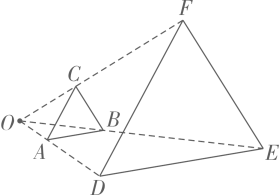 A、 B、 C、 D、6. 按如图所示的规律搭正方形:搭一个小正方形需要根小棒,搭两个小正方形需要根小棒,则搭个这样的小正方形需要的小棒数量为( )
A、 B、 C、 D、6. 按如图所示的规律搭正方形:搭一个小正方形需要根小棒,搭两个小正方形需要根小棒,则搭个这样的小正方形需要的小棒数量为( ) A、 B、 C、 D、7. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间8. 如图,某小区居民休闲娱乐中心是一块长方形长米,宽米场地,被条宽度相等的绿化带分为总面积为平方米的活动场所,如果设绿化带的宽度为米,由题意可列方程为( )
A、 B、 C、 D、7. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间8. 如图,某小区居民休闲娱乐中心是一块长方形长米,宽米场地,被条宽度相等的绿化带分为总面积为平方米的活动场所,如果设绿化带的宽度为米,由题意可列方程为( )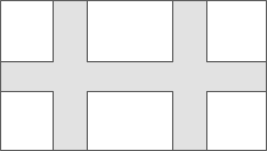 A、 B、
A、 B、
C、 D、9. 如图,是的直径,是的切线,连接交于点 , 连接 , , , 则的长为( ) A、
A、
B、
C、
D、10. 对于若干个数,先将每两个数作差,再将这些差的绝对值相加,这样的运算称为对这若干个数进行“绝对运算”例如,对于 , , 进行“绝对运算”,得到: .
对 , , , 进行“绝对运算”的结果是;
对 , , 进行“绝对运算”的结果为 , 则的最小值是;
对 , , , 进行“绝对运算”,化简的结果可能存在种不同的表达式;
以上说法中正确的个数为( )A、 B、 C、 D、二、填空题(本大题共8小题,共32.0分)
-
11. 计算: .12. 如图, , , 则为 度
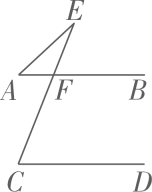 13. 一个n边形的内角和是720°,则n= .14. 从、、中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是偶数的概率是 .15. 如图,在菱形中, , 以为圆心,为半径画弧,则图中阴影部分的面积为 .
13. 一个n边形的内角和是720°,则n= .14. 从、、中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是偶数的概率是 .15. 如图,在菱形中, , 以为圆心,为半径画弧,则图中阴影部分的面积为 . 16. 如图,在边长为的菱形中, , 点是边的中点,连接 , 将菱形翻折,使点落在线段上的点处,折痕交于点 , 则线段的长为 .
16. 如图,在边长为的菱形中, , 点是边的中点,连接 , 将菱形翻折,使点落在线段上的点处,折痕交于点 , 则线段的长为 .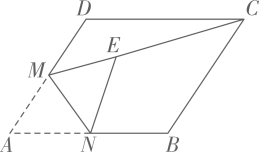 17. 若关于的一元一次不等式组有解,且关于的分式方程的解为整数,则所有满足条件的整数的值之和是 .18. 把一个四位数的各个数位上的数字均不为零之和记为 , 把的千位数字与百位数字的乘积记为 , 十位数字与个位数字的乘积记为 , 称为的“陪伴值”.(1)、的“陪伴值”为 ;
17. 若关于的一元一次不等式组有解,且关于的分式方程的解为整数,则所有满足条件的整数的值之和是 .18. 把一个四位数的各个数位上的数字均不为零之和记为 , 把的千位数字与百位数字的乘积记为 , 十位数字与个位数字的乘积记为 , 称为的“陪伴值”.(1)、的“陪伴值”为 ;
(2)、若的千位与个位数字之和能被整除,且 , 的“陪伴值”为 , 则满足条件的的最小值是 .三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:
(1)、;
(2)、 .20. 在学习直角三角形的过程中,小明遇到了一个问题:在直角三角形中, , 平分 , 探究 , , , 是否成比例线段,小明的思路是:首先过点作的垂线,从而构造与全等的三角形,再通过三角形面积建立等量关系,使问题得到解决请根据小明的思路完成下面的作图与填空: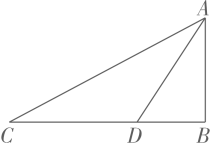
尺规作图:过点作于点用基本作图,保留作图痕迹,不写作法、结论 .
证明:平分 ,
▲ ,
,
▲ ,
,
在和中,
,
≌ ,
▲ ,
又 ,
,
▲ ,
即 ,
, , , 为成比例线段.21. 为了增加学生对航天航空知识的了解,学校组织全校学生收看了“天宫课堂”系列科普视频,并进行了一次航天知识竞赛,现从初一、初二年级各随机抽取了名同学的成绩,得分用表示,共分成组:: , : , : , : , 对得分进行整理分析,给出了下面部分信息:
初一年级航天知识竞赛成绩在组中的数据为: , , .
初二年级航天知识竞赛成绩: , , , , , , , , , , , , , , .
航天知识竞赛成绩统计表:年级
平均数
中位数
最高分
众数
初一
初二
 (1)、 , ;(2)、通过以上数据分析,你认为哪个年级的学生掌握航天航空知识的情况更好?并说明理由写出一条理由即可 .(3)、若初一、初二两个年级共有名学生,请估计初一和初二两个年级此次知识竞赛成绩达到分及以上的学生一共有多少人?22. 小区便民超市分别用元和元购进若干箱纯牛奶和酸奶,已知此次购进的酸奶的数量是纯牛奶数量的倍,且每箱酸奶的价格比每箱纯牛奶的价格贵元.(1)、求此次购进纯牛奶的数量.
(1)、 , ;(2)、通过以上数据分析,你认为哪个年级的学生掌握航天航空知识的情况更好?并说明理由写出一条理由即可 .(3)、若初一、初二两个年级共有名学生,请估计初一和初二两个年级此次知识竞赛成绩达到分及以上的学生一共有多少人?22. 小区便民超市分别用元和元购进若干箱纯牛奶和酸奶,已知此次购进的酸奶的数量是纯牛奶数量的倍,且每箱酸奶的价格比每箱纯牛奶的价格贵元.(1)、求此次购进纯牛奶的数量.
(2)、在销售过程中,纯牛奶每箱售价是元,很快售完;酸奶每箱按进价加价销售,售出一部分后,恰逢五一假期,商场搞促销活动,决定打九折出售剩余的酸奶,已知纯牛奶和酸奶全部售出后共获利元,求有多少箱酸奶打九折出售?23. 如图,海面上 , 两个小岛同时接到消息,一艘客船在地发生故障,需要支援,经测量,和分别位于的正北方向和南偏东方向;在点的北偏西方向上,已知 , 两地相距海里.
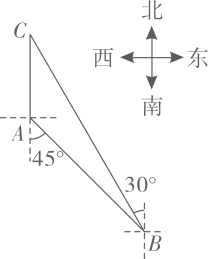 (1)、求 , 两地之间的距离结果保留根号;(2)、位于岛的补给船和救援船接到消息后同时出发前往地,补给船以每小时海里的速度从地出发,沿方向前往地,救援船以每小时海里的速度从地出发沿方向前往地准备救援材料准备材料的时间为分钟 , 再以相同的速度沿方向前往地,请通过计算说明哪艘船会先到达地.
(1)、求 , 两地之间的距离结果保留根号;(2)、位于岛的补给船和救援船接到消息后同时出发前往地,补给船以每小时海里的速度从地出发,沿方向前往地,救援船以每小时海里的速度从地出发沿方向前往地准备救援材料准备材料的时间为分钟 , 再以相同的速度沿方向前往地,请通过计算说明哪艘船会先到达地.
参考数据: , ,24. 如图,在中, , , , 点是的中点,动点从点出发,沿着折线含端点和运动,速度为每秒个单位长度,到达点停止运动,设点的运动时间为秒,点到的距离为个单位长度.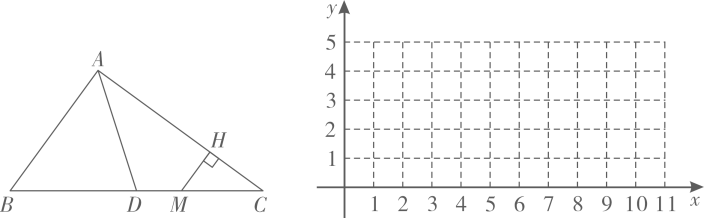 (1)、求关于的函数关系式,并写出自变量的取值范围.(2)、在直角坐标系中画出与的函数图象,并写出它的一条性质 .(3)、根据图象直接写出当时的取值范围: .25. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 .
(1)、求关于的函数关系式,并写出自变量的取值范围.(2)、在直角坐标系中画出与的函数图象,并写出它的一条性质 .(3)、根据图象直接写出当时的取值范围: .25. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 .
(1)、求该抛物线的函数表达式;(2)、点为线段下方抛物线上的一动点,过点作轴交直线于点 , 为上一点,且 , 求的最大值及此时点的坐标;(3)、在的条件下,将抛物线沿射线方向平移,得到新抛物线 , 新抛物线和原抛物线交于点 , 与轴交于点 , 点是新抛物线对称轴上的一点,若是以为腰的等腰三角形,写出所有符合条件的点的坐标,并写出求解点的坐标的其中一种情况的过程.26. 在中, , 于点 .
(1)、如图 , 过点作 , 分别交 , 于 , , 求证:;(2)、如图 , 过点作交于点 , 点为左侧一点,且 , 连接 , , 猜想线段 , , 之间存在的数量关系,并证明你的猜想;(3)、如图 , , , 点为内部一点,直接写出的最小值.