甘肃省定西市岷县、临洮县2023年中考模拟数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 下列各式中结果为负数的是( )A、 B、 C、 D、3. 如图,直线 , , 则等于( )
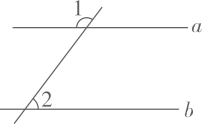 A、 B、 C、 D、4. 围棋起源于中国.古代称之为“弈”,至今已有多年历史.年月,世界围棋冠军柯洁与人工智能机器人进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、
A、 B、 C、 D、4. 围棋起源于中国.古代称之为“弈”,至今已有多年历史.年月,世界围棋冠军柯洁与人工智能机器人进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、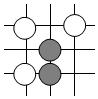 B、
B、 C、
C、 D、
D、 5. 下列式子计算正确的是( )A、 B、 C、 D、6. 网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶据预测,年到年中国直接经济产出和间接经济产出的情况如图所示根据如图提供的信息,下列推断不合理的是( )
5. 下列式子计算正确的是( )A、 B、 C、 D、6. 网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶据预测,年到年中国直接经济产出和间接经济产出的情况如图所示根据如图提供的信息,下列推断不合理的是( )
 A、年间接经济产出比直接经济产出多万亿元 B、年到年直接经济产出和间接经济产出都是逐年增长 C、年到年与年到年间接经济产出的增长率相同 D、年直接经济产出约为年直接经济产出的倍7. 如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是( )
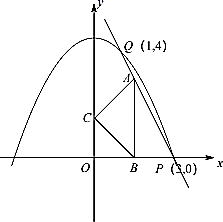
A、年间接经济产出比直接经济产出多万亿元 B、年到年直接经济产出和间接经济产出都是逐年增长 C、年到年与年到年间接经济产出的增长率相同 D、年直接经济产出约为年直接经济产出的倍7. 如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是( ) A、5m B、12m C、13m D、18m8. 如图,直线与轴、轴分别交于、两点,绕点顺时针旋转后得到 , 则点的对应点坐标为( )
A、5m B、12m C、13m D、18m8. 如图,直线与轴、轴分别交于、两点,绕点顺时针旋转后得到 , 则点的对应点坐标为( ) A、 B、 C、 D、9. 如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是( )
A、 B、 C、 D、9. 如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是( ) A、πm2 B、πm2 C、πm2 D、πm210. 如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为 , 线段的长为 , 如果与的函数图象如图所示,则矩形的面积是( )
A、πm2 B、πm2 C、πm2 D、πm210. 如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为 , 线段的长为 , 如果与的函数图象如图所示,则矩形的面积是( ) A、60 B、48 C、24 D、12
A、60 B、48 C、24 D、12二、填空题(本大题共6小题,共18.0分)
-
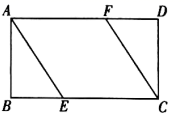
11. 分解因式: .12. 若关于 的一元二次方程 有两个相等的实数根,则 的值为 .13. 如图,在矩形 中,点 分别在 上, .只需添加一个条件即可证明四边形 是菱形,这个条件可以是(写出一个即可).
 14. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数的点为圆心,正方形对角线的长为半径画半圆,交数轴于点和点 , 则点表示的数是 .
14. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数的点为圆心,正方形对角线的长为半径画半圆,交数轴于点和点 , 则点表示的数是 .
 15. 声音在空气中的传播速度与温度的关系如表:
15. 声音在空气中的传播速度与温度的关系如表:温度
速度
则速度与温度之间的关系式为 ;当时,声音的传播速度为 .
16. 如图,点A、B、C在 上, , ,则 的半径为.
三、解答题(本大题共11小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:18. 解不等式组: ,并将解集在数轴上表示出来.
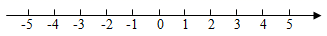 19. 已知: ,求代数式 的值.20. 作图题要求:尺规作图,写出作法并保留作图痕迹
19. 已知: ,求代数式 的值.20. 作图题要求:尺规作图,写出作法并保留作图痕迹
已知:线段、 .
求作:等腰 , 使 , , 边上的高 .
21. 小红和小丁玩纸牌游戏:如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌上,小红先从中抽出一张,小丁从剩余的3张牌中也抽出一张.比较两人抽出的牌面上的数字,数字大者获胜. (1)、请用树状图或列表法表示出两人抽牌可能出现的所有结果;(2)、这个游戏公平吗?请说明理由.22.
(1)、请用树状图或列表法表示出两人抽牌可能出现的所有结果;(2)、这个游戏公平吗?请说明理由.22.风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
 23. 月日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
23. 月日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
一、数据收集,从全校随机抽取学生,进行每周用于课外阅读时间的调查,数据如下单位::二、整理数据,按如下分段整理样本数据并补全表格:
课外阅读时间
等级
人数
三、分析数据,补全下列表格中的统计量:
平均数
中位数
众数
四、得出结论:
表格中的数据: ▲ , ▲ , ▲ ;
用样本中的统计量估计该校学生每周用于课外阅读时间的等级为 ▲ ;
如果该校现有学生人,估计等级为“”的学生有 ▲ 人;
假设平均阅读一本课外书的时间为分钟,请你用样本平均数估计该校学生每人一年按周计算平均阅读 ▲ 本课外书.24. 如图,已知反比例函数的图象与一次函数的图象交于点 , 点 . (1)、求和的值;(2)、求的面积;(3)、直接写出一次函数值大于反比例函数值的自变量的取值范围.25. 如图,是的直径, , 分别与相切于点 , , 连接 , 点在的延长线上,延长 , 交于点 .
(1)、求和的值;(2)、求的面积;(3)、直接写出一次函数值大于反比例函数值的自变量的取值范围.25. 如图,是的直径, , 分别与相切于点 , , 连接 , 点在的延长线上,延长 , 交于点 .
 (1)、求证:;(2)、若 , , , 求的长.
(1)、求证:;(2)、若 , , , 求的长.