甘肃省武威市2023年中考一模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 2023的绝对值为( )A、2023 B、 C、 D、2. 一个等腰三角形的顶角是 , 则它的底角的大小是( )A、 B、 C、 D、3. 代数式有意义,则的取值范围是( )A、 B、 C、且 D、且4. 关于的方程的两个实数根分别为和 , 则分解因式等于( )A、 B、 C、 D、5. 如图,在中,、分别是和上的点, , 若 , 那么( )
 A、
A、
B、
C、
D、6. 垃圾分类是对垃圾进行有效处置的一种科学管理方式,是对垃圾收集处置传统方式的改革,甲乙两班各有名同学参加了学校组织的年“生活垃圾分类回收”的考试考试规定成绩大于等于分为优异,两个班成绩的平均数、中位数、方差如表所示,则下列说法正确的是( )参加人数
平均数
中位数
方差
甲
乙
A、甲班的成绩比乙班的成绩稳定 B、小高得分将排在甲班的前名
C、甲、乙两班竞赛成绩的众数相同 D、甲班成绩优异的人数比乙班多7. 生活中处处有数学,多边形在生活中的应用更是不胜枚举如图是一个正六边形的螺帽,它的边长是 , 则这个正六边形的半径和扳手的开口的值分别是( ) A、 , B、 , C、 , D、 ,8. 为响应承办“绿色奥运”的号召,某校计划组织七年级部分同学参加义务植树棵由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了 , 结果每人比原计划少栽了棵若设原计划有人参加这次植树活动,则根据题意可列出方程为( )A、 B、 C、 D、9. 如图,是半圆的直径,是的中点,过点作 , 交半圆于点 , 则与的长度的比为( )
A、 , B、 , C、 , D、 ,8. 为响应承办“绿色奥运”的号召,某校计划组织七年级部分同学参加义务植树棵由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了 , 结果每人比原计划少栽了棵若设原计划有人参加这次植树活动,则根据题意可列出方程为( )A、 B、 C、 D、9. 如图,是半圆的直径,是的中点,过点作 , 交半圆于点 , 则与的长度的比为( ) A、: B、: C、: D、:10. 如图 , 在矩形的边上有一点 , 连结 , 点从顶点出发,沿以的速度匀速运动到点图是点运动时,的面积随时间变化的函数图象,则的长为( )
A、: B、: C、: D、:10. 如图 , 在矩形的边上有一点 , 连结 , 点从顶点出发,沿以的速度匀速运动到点图是点运动时,的面积随时间变化的函数图象,则的长为( )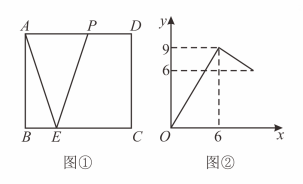 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 计算: .12. 因式分解: .13. 若方程是关于的一元一次方程,则 .14. 如图,已知矩形 的对角线 的长为 ,顺次连结各边中点 、 、 、 得四边形 ,则四边形 的周长为 .
 15. 如图, , , 是上的三个点, , 则的度数是 .
15. 如图, , , 是上的三个点, , 则的度数是 .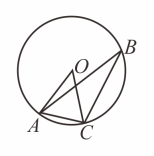 16. 某机器零件的尺寸标注如图所示,在其主视图,左视图和俯视图中,既是轴对称图形又是中心对称图形的是 .
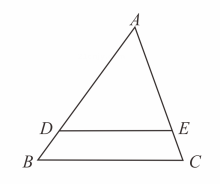
16. 某机器零件的尺寸标注如图所示,在其主视图,左视图和俯视图中,既是轴对称图形又是中心对称图形的是 .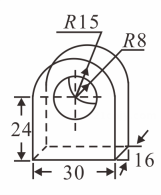 17. “水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的如图 , 水柱的最高点为 , , , 水嘴高 , 则水柱落地点到水嘴所在墙的距离是
17. “水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的如图 , 水柱的最高点为 , , , 水嘴高 , 则水柱落地点到水嘴所在墙的距离是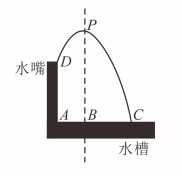 18. 如图,在矩形纸片中, , , 点在上,将沿折叠,使点落在对角线上的点处,则的长为 .
18. 如图,在矩形纸片中, , , 点在上,将沿折叠,使点落在对角线上的点处,则的长为 .
三、计算题(本大题共1小题,共6.0分)
-
19. 计算: .
四、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 化简: .21. 如图,已知中, .
 (1)、作图:在上找一点 , 使得点到、两边的距离相等;尺规作图,保留痕迹(2)、若的垂直平分线交线段于点 , 且的周长是 , , 则 .22. 线上教学期间,很多同学采用笔记本电脑学习,九年级一班同学为保护眼睛,开展实践探究活动如图,当张角时,顶部边缘处离桌面的高度的长为 , 此时用眼舒适度不太理想小组成员调整张角大小继续探究,最后联系黄金比知识发现当张角时点是的对应点 , 用眼舒适度较为理想求此时顶部边缘处离桌面的高度的长结果精确到;参考数据: , ,
(1)、作图:在上找一点 , 使得点到、两边的距离相等;尺规作图,保留痕迹(2)、若的垂直平分线交线段于点 , 且的周长是 , , 则 .22. 线上教学期间,很多同学采用笔记本电脑学习,九年级一班同学为保护眼睛,开展实践探究活动如图,当张角时,顶部边缘处离桌面的高度的长为 , 此时用眼舒适度不太理想小组成员调整张角大小继续探究,最后联系黄金比知识发现当张角时点是的对应点 , 用眼舒适度较为理想求此时顶部边缘处离桌面的高度的长结果精确到;参考数据: , ,
 23. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的 , , , 四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到小区的概率是 ;(2)、请用列表或画树状图的方法求甲组抽到小区,同时乙组抽到小区的概率.24. 受疫情影响,年下半学期很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动,为了解学生上网课使用的设备类型,某校从“电脑,手机,电视,其他”四种类型的设备对学生进行了一次抽样调查;调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图:
23. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的 , , , 四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到小区的概率是 ;(2)、请用列表或画树状图的方法求甲组抽到小区,同时乙组抽到小区的概率.24. 受疫情影响,年下半学期很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动,为了解学生上网课使用的设备类型,某校从“电脑,手机,电视,其他”四种类型的设备对学生进行了一次抽样调查;调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图: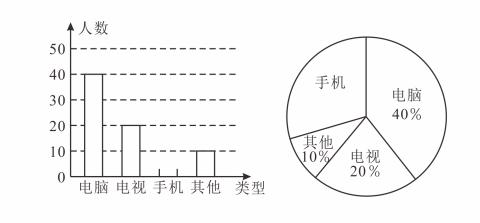
请根据以上信息解答下列问题:
(1)、本次调查抽取的总人数是 人,在扇形统计图中,“电视”所对应的扇形的圆心角的度数为 ;(2)、补全条形统计图;(3)、该校九年级共有名学生,估计有多少名同学用电脑上课?25. 如图,直线与反比例函数的图象交于 , 两点.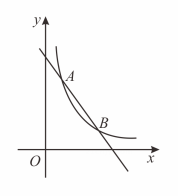 (1)、求的值;(2)、在轴上找一点 , 连接 , , 使的值最小,求点的坐标.26. 如图,点、、在上, , 直线 , , 点在上.
(1)、求的值;(2)、在轴上找一点 , 连接 , , 使的值最小,求点的坐标.26. 如图,点、、在上, , 直线 , , 点在上.
 (1)、判断直线与的位置关系,并说明理由;(2)、若的半径为 , 求弦的长.
(1)、判断直线与的位置关系,并说明理由;(2)、若的半径为 , 求弦的长.
-