甘肃省平凉四中2023年中考三模中考数学试卷

试卷更新日期：2023-09-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. $- 4$ 的相反数（）

A、 $\frac{1}{4}$ B、 $4$ C、 $- 4$ D、 $\pm 4$

查看试题解析
2. 下列既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 近年来出生人口持续走低，即使国家开放三胎，也缓解不了颓势， $2022$ 年我国出生人口是 $1062$ 万人，数据 $1062$ 万用科学记数法表示应为（）

A、 $1062 \times 1 0^{4}$ B、 $10.62 \times 1 0^{6}$ C、 $1.062 \times 1 0^{7}$ D、 $0.1062 \times 1 0^{8}$

查看试题解析
4. 关于 $x$ 的一元二次方程 $x^{2} + 4 x + k = 0$ 有两个实数根，则 $k$ 的取值范围是（）

A、 $k \leq - 4$ B、 $k < - 4$ C、 $k \leq 4$ D、 $k < 4$

查看试题解析
5. 如图， $A B / / C D$ ，点 $E$ 在 $B C$ 上，若 $∠ 1 = 40 °$ ， $∠ 2 = 20 °$ ，则 $∠ 3$ 的度数是（）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $50 °$

查看试题解析
6. 直线 $y = k x + b$ 经过一、三、四象限，那么点 $(b ， k)$ 在第几象限．（）

A、四 B、三 C、二 D、一

查看试题解析
7. 如图，已知 $A B$ 是 $⊙ O$ 的直径， $C D$ 是弦，若 $∠ B C D = 36 °$ ，则 $∠ A B D$ 等于（）

A、 $54 °$ B、 $56 °$ C、 $64 °$ D、 $66 °$

查看试题解析
8. 我国古代著作 $《$ 四元玉鉴 $》$ 记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意为：现请人代买一批椽，这批椽的价钱为 $6210$ 文．如果每株椽的运费是 $3$ 文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问 $6210$ 文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
9. 道路施工部门在铺设如图所示的管道时，需要先按照其中心线计算长度后再备料．图中的管道中心线 $\overset{�}{A B}$ 的长为 $($ 单位： $m)$ （）

A、 $\frac{40 π}{3}$
B、 $\frac{80 π}{3}$
C、 $\frac{1600 π}{3}$
D、 $\frac{3200 π}{3}$

查看试题解析
10. 如图 $(1)$ ， ▱ $A B C D$ 中， $A B = 3$ ， $B D ⊥ A B$ ，动点 $F$ 从点 $A$ 出发，沿折线 $A D B$ 以每秒 $1$ 个单位长度的速度运动到点 $B .$ 图 $(2)$ 是点 $F$ 运动时， $△ F B C$ 的面积 $y$ 随时间 $x$ 变化的图象，则 $m$ 的值为（）

A、 $6$ B、 $10$ C、 $12$ D、 $20$

查看试题解析

二、填空题（本大题共8小题，共32.0分）

11. 当x时，分式 $\frac{x + 2}{x - 1}$ 有意义.

查看试题解析
12. 因式分解： $x^{3} - x$ = ．

查看试题解析
13. 若点 $(m ， n)$ 在函数 $y = 2 x + 1$ 的图象上，则 $2 m - n$ 的值是．

查看试题解析
14. 如图，在 $6 \times 4$ 网格中建立平面直角坐标系，使点 $A$ 的坐标为 $(1 ， 2)$ ，点 $B$ 的坐标为 $(- 1 ， - 1)$ ，则点 $C$ 的坐标为．

查看试题解析
15. 如图，在▱ABCD中，对角线AC与BD相交于点O，请添加一个条件，使▱ABCD成为菱形（写出符合题意的一个条件即可）

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 为 $A B$ 中点， $C D = 5$ ， $A C = 6$ ，则 $B C$ 长为．

查看试题解析
17. 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线 $.$ 若不考虑空气阻力，小球的飞行高度 $h ($ 单位： $m)$ 与飞行时间 $t ($ 单位： $s)$ 之间具有函数关系： $h = - 5 t^{2} + 20 t$ ，则小球飞行最大高度是 $m .$

查看试题解析
18. 如图，点 $E$ 是矩形 $A B C D$ 中 $C D$ 边上一点， $△ B C E$ 沿 $B E$ 折叠得到对应的 $△ B F E$ ，且点 $C$ 的对应点 $F$ 落在 $A D$ 上．若 $t a n ∠ D F E = \frac{5}{12}$ ， $B C = 3$ ，则 $C E =$ ．

查看试题解析

三、解答题（本大题共10小题，共88.0分。解答应写出文字说明，证明过程或演算步骤）

19. 计算： $5 - (π - 3.14)^{0} + 4 s i n 60 ° - | 1 - \sqrt{3} |$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} x + 2 \geq 1 ① \\ 2 x \leq x + 3 ② \end{array}$ ．
请结合题意填空，完成本题的解答．
⑴解不等式 $①$ ，得     ▲     ；
⑵解不等式 $②$ ，得     ▲   ；
⑶ 把不等式 $①$ 和 $②$ 的解集在数轴上表示出来；
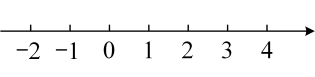
⑷原不等式组的解集为     ▲   ．

查看试题解析
21. 如图，已知 $△ A B C$ ．

⑴请用尺规作图作出 $∠ B A C$ 的平分线交 $B C$ 于点 $D$ ；
⑵请用尺规作图作出线段 $A D$ 的垂直平分线交 $A B$ 于点 $E$ ，交 $A C$ 于点 $F$ ；
⑶连接 $D E$ 和 $D F$ ，直接写出四边形 $A E D F$ 的形状．

查看试题解析
22. 钓鱼岛是我国固有领土， $2021$ 年 $4$ 月 $26$ 日，中华人民共和国自然资源部在其官网上公布 $《$ 钓鱼岛及其附属岛屿地形地貌调查报告 $》$ ，报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据．如图所示，点 $A$ 是岛上最西端“西钓角”，点 $B$ 是岛上最东端“东钓角”， $A B$ 长约 $3641$ 米，点 $D$ 是岛上的小黄鱼岛，且 $A$ 、 $B$ 、 $D$ 三点共线．某日中国海监一艘执法船巡航到点 $C$ 处时，恰好看到正北方的小黄鱼岛 $D$ ，并测得 $∠ A C D = 70 °$ ， $∠ B C D = 45 ° .$ 根据以上数据，请求出此时执法船距离小黄鱼岛 $D$ 的距离 $C D$ 的值． $($ 参考数据： $t a n 70 ° \approx 2.75$ ， $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ，结果精确到 $1$ 米． $)$

查看试题解析
23. 新冠疫情防控期间，武威市某学校学生进校园必须戴口罩，测体温，该校开通了三条测温通道，分别为：红外热成像测温 $(A$ 通道 $)$ 和人工测温 $(B$ 通道和 $C$ 通道 $) .$ 在三条通道中，每位同学都只能随机选择其中一条通道．某天早晨，该校学生小红和小明将随机选择一条测温通道进人校园．

(1)、小红选择从红外热成像测温通道进人校园的概率为；

(2)、用列表法或树状图表示小红和小明选择不同的测温通道进人校园的概率．

查看试题解析
24. 中考改革是为了进一步推进高中阶段学校考试招生制度，某市在初中毕业生学业考试、综合素质评价、高中招生录取等方面进行了积极探索，对学生各科成绩实行等级制，即 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 五个等级，根据某班一次数学模拟考试成绩按照等级制绘制了两幅统计图 $($ 均不完整 $)$ ，
请根据统计图提供的信息解答下列问题．

(1)、本次模拟考试该班学生有人；

(2)、补全条形统计图；

(3)、本次模拟考试该班学生考试成绩等级的中位数在等级；

(4)、该校共有 $1000$ 名学生，根据统计图估计该校 $A$ 等级的学生人数．

查看试题解析
25. 如图，一次函数 $y = k x + b$ 的图象与 $x$ 轴正半轴相交于点 $C$ ，与反比例函数 $y = - \frac{2}{x}$ 的图象相交于点 $A (- 1 ， m)$ 和点 $B$ ，过点 $A$ 作 $A D ⊥ x$ 轴，垂足为 $D$ ，且 $A D = C D$ ．

(1)、求一次函数的解析式；

(2)、连接 $B D$ ，求 $△ A B D$ 的面积．

查看试题解析
26. 如图， $A B$ 是 $⊙ O$ 的直径，点C是 $⊙ O$ 上异于A、B的点，连接 $A C$ 、 $B C$ ，点D在 $B A$ 的延长线上，且 $∠ D C A = ∠ A B C$ ，点E在 $D C$ 的延长线上，且 $B E ⊥ D C$ ．

(1)、求证： $D C$ 是 $⊙ O$ 的切线：

(2)、若 $\frac{O A}{O D} = \frac{2}{3} ， B E = 3$ ，求 $D A$ 的长．

查看试题解析
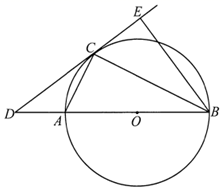27. 问题情境：数学活动课上，老师组织同学们以“正方形”为主题开展数学活动．

(1)、动手实践：如图 $①$ ，已知正方形纸片 $A B C D$ ，勤奋小组将正方形纸片沿过点 $A$ 的直线折叠，使点 $B$ 落在正方形 $A B C D$ 的内部，点 $B$ 的对应点为点 $M$ ，折痕为 $A E$ ，再将纸片沿过点 $A$ 的直线折叠，使 $A D$ 与 $A M$ 重合，折痕为 $A F$ ，易知点 $E$ 、 $M$ 、 $F$ 共线，则 $∠ E A F =$ 度．

(2)、拓展应用：如图 $②$ ，腾飞小组在图 $①$ 的基础上进行如下操作：将正方形纸片沿 $E F$ 继续折叠，使得点 $C$ 的对应点为点 $N$ ，他们发现，当点 $E$ 的位置不同时，点 $N$ 的位置也不同，当点 $E$ 在 $B C$ 边的某一位置时，点 $N$ 恰好落在折痕 $A E$ 上．
$①$ 则 $∠ C F E =$ 度．
$②$ 设 $A M$ 与 $N F$ 的交点为点 $P$ ，运用 $(1)$ 、 $(2)$ 操作所得结论，求证： $△ A N P$ ≌ $△ F N E$ ．

(3)、解决问题：在图 $②$ 中，若 $A B = 3$ ，请直接写出线段 $M P$ 的长．

查看试题解析
28. 如图，在平面直角坐标系中，抛物线 $y = - \frac{1}{3} x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ，点 $D$ 是点 $C$ 关于 $x$ 轴的对称点．

(1)、求抛物线与直线 $B D$ 的解析式；

(2)、点 $P$ 为直线 $B C$ 上方抛物线上一动点，当 $△ B P C$ 的面积最大时，求点 $P$ 的坐标；

(3)、在 $(2)$ 的条件下，当 $△ B P C$ 的面积最大时，在抛物线的对称轴上有一动点 $M$ ，在 $B D$ 上有一动点 $N$ ，且 $M N ⊥ B D$ ，求 $P M + M N$ 的最小值．

查看试题解析