新疆乌鲁木齐市2023年中考二模数学考试试卷

试卷更新日期：2023-09-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共9小题，共45.0分。在每小题列出的选项中，选出符合题目的一项）

1. 比 $- 2$ 大 $3$ 的数是（）

A、 $5$ B、 $1$ C、 $0$ D、 $- 5$

查看试题解析
2. 六个大小相同的正方体搭成的几何体如图所示，其主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列算式中，结果等于 $4 a^{4}$ 的是（）

A、 $2 a^{2} + 2 a^{2}$ B、 $3 a^{2} \cdot a^{2}$ C、 $a^{5} \div 4 a$ D、 ${(- 2 a^{2})}^{2}$

查看试题解析
4. 在今年“双 $11$ ”来临之际，某品牌鞋专柜为更好的备货，特整理了前期销售这款鞋子尺码的平均数、中位数、众数、方差，其中作为销售主管最关心的数据是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 如图，直角三角板的直角顶点放在直线 $b$ 上，且 $a / / b$ ， $∠ 1 = 55 °$ ，则 $∠ 2$ 的度数为（）

A、 $25 °$ B、 $35 °$ C、 $45 °$ D、 $55 °$

查看试题解析
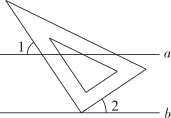6. 我国古代数学名著 $《$ 孙子算经 $》$ 中有一问题：“今三人共车，两车空；二人共车，九人步 $.$ 问人与车各几何？”其大意为：现有若干人和车，若每辆车乘坐 $3$ 人，则空余两辆车；若每辆车乘坐 $2$ 人，则有 $9$ 人步行 $.$ 问人与车各多少？设有 $x$ 人， $y$ 辆车，则所列方程组正确的是（）

A、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x}{2} - 9 = y \end{array}$ B、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x - 9}{2} = y \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x - 9}{2} = y \end{array}$ D、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x}{2} + 9 = y \end{array}$

查看试题解析
7. 如图， $A$ 、 $B$ 、 $C$ 三点在正方形网格的格点上，若将 $△ A C B$ 绕点 $A$ 逆时针旋转得到 $△ A C' B'$ ，则 $c o s ∠ B'$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{17}}{17}$ C、 $\frac{4 \sqrt{17}}{17}$ D、 $\frac{\sqrt{17}}{5}$

查看试题解析
8. 如果 $a^{2} + 3 a - 2 = 0$ ，那么代数式 $(\frac{3}{a^{2} - 9} + \frac{1}{a + 3}) \cdot \frac{a - 3}{a^{2}}$ 的值为（）

A、 $1$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
9. 如图，在边长为 $4$ 的正方形 $A B C D$ 中， $P$ 是 $B C$ 边上一动点 $($ 不含 $B$ ， $C$ 两点 $)$ ，将 $△ A B P$ 沿直线 $A P$ 翻折，点 $B$ 落在点 $E$ 处；在 $C D$ 上有一点 $M$ ，使得将 $△ C M P$ 沿直线 $M P$ 翻折后，点 $C$ 落在直线 $P E$ 上的点 $F$ 处，直线 $P E$ 交 $C D$ 于点 $N$ ，连接 $M A$ ， $N A .$ 则以下结论中正确的是（）

$①$ 线段 $A M$ 长度的最小值为 $5$ ；
$②$ 四边形 $A M C B$ 的面积最大值为 $10$ ；
$③$ 当 $△ A B P$ ≌ $△ A D N$ 时， $B P = 4 \sqrt{2} - 4$ ；
$④$ 当 $P$ 为 $B C$ 中点时， $A E$ 是线段 $N P$ 的垂直平分线．

A、 $① ② ③$ B、 $① ② ④$ C、 $① ③ ④$ D、 $② ③ ④$

查看试题解析

二、填空题（本大题共6小题，共30.0分）

10. 红细胞的直径约为 $0.0000077 m$ ， $0.0000077$ 用科学记数法表示为．

查看试题解析
11. 不等式组 ${\begin{array}{l} x - 2 \geq 0 \\ 2 x - 5 < 1 \end{array}$ 的解集是．

查看试题解析
12. 不透明袋子中装有除颜色外都相同的 $7$ 个小球，其中白球 $3$ 个，黑球 $4$ 个 $.$ 从中任意摸出的一个小球恰为白球的概率为．

查看试题解析
13. 圆锥的母线长为 $12 c m$ ，其侧面展开图的圆心角为 $150 °$ ，则圆锥的底面圆半径长是 $c m$ ．

查看试题解析
14. 已知点 $A (2 ， y_{1})$ ， $B (3 ， y_{2})$ 在反比例函数 $y = \frac{k^{2} + 2}{x} (k$ 为常数 $)$ 的图象上，则 $y_{1}$ 与 $y_{2}$ 的大小关系为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，分别以点 $A$ 和 $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ，作直线 $M N$ 交 $A B$ 于点 $E$ ，交 $B C$ 于点 $F .$ 若 $\frac{C F}{B F} = \frac{3}{5}$ ，则 $t a n ∠ A B C$ 的值为．

查看试题解析

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）

16. 计算： $4 c o s 30 ° + | - 4 | - \sqrt{12} + (π - 3)^{0}$ ．

查看试题解析
17. 先化简，再求值： $(a + b)^{2} - a (a - b) + (a - b) (a + b)$ ，其中 $a = \sqrt{2}$ ， $b = - 1$ ．

查看试题解析
18. 如图，▱ $A B C D$ 中，点 $O$ 为对角线 $A C$ 的中点， $E F$ 过点 $O$ 且分别交 $A D$ ， $B C$ 于点 $E$ ， $F$ ，连接 $A F$ ， $C E$ ．

(1)、求证： $△ A O E$ ≌ $△ C O F$ ；

(2)、求证：若 $A C$ 平分 $∠ E A F$ ，四边形 $A E C F$ 为菱形．

查看试题解析
19. 我市为加快推进生活垃圾分类工作，对分类收集桶实行统一的外型、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶 $.$ 为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如图所示的两幅不完整的统计图．
根据图中信息，解答下列问题：

(1)、此次调查一共随机采访了名学生，在扇形统计图中，“灰”所在扇形的圆心角的度数为；

(2)、补全条形统计图 $($ 要求在条形图上方注明人数 $)$ ；

(3)、若该校有 $1800$ 名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；

(4)、李老师计划从 $A$ ， $B$ ， $C$ ， $D$ 四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图法或列表法求出恰好抽中 $A$ ， $B$ 两人的概率．

查看试题解析
20. 某商场销售每件进价为 $50$ 元的一种商品，物价部门规定每件售价不得高于 $80$ 元，经市场调查，发现每月的销售量 $y ($ 件 $)$ 与每件的售价 $x ($ 元 $)$ 满足 $y = - 2 x + 240$ ．

(1)、商场每月想从这种商品销售中获利 $2250$ 元，该如何给这种商品定价？

(2)、请问售价定为多少元时可获得月最大利润？最大利润是多少？

查看试题解析
21. 如图，某公园里的四条人行步道围成四边形 $A B C D$ ，经测量，点 $C$ 在点 $B$ 的正北方向，点 $D$ 在点 $C$ 的北偏西 $60 °$ ，点 $A$ 在点 $B$ 的正西方向，点 $D$ 在点 $A$ 的东北方向， $A B = 700 m$ ， $C D = 200 \sqrt{3} m$ ，求 $A D$ 的长 $. ($ 结果保留根号 $)$

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 是 $\overset{⏜}{B C}$ 的中点， $∠ P A C = ∠ A D C$ ，且 $C D = \sqrt{5}$ ， $A D$ 与 $B C$ 交于点 $E$ ．

(1)、求证： $P A$ 是 $⊙ O$ 的切线；

(2)、若 $t a n ∠ C A D = \frac{1}{3}$ ，求 $D E$ 的长；

(3)、延长 $C D$ 、 $A B$ 交于点 $F$ ，若 $O B = B F$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 如图，已知抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $B (- 1 ， 0)$ ， $C (5 ， 0)$ ．

(1)、求抛物线的解析式及顶点 $M$ 的坐标；

(2)、如图 $2$ ，点 $E$ 在抛物线的对称轴上，且位于 $x$ 轴的上方，将 $△ B C E$ 沿直线 $B E$ 翻折，如果点 $C$ 的对应点 $F$ 恰好落在抛物线的对称轴上，求点 $E$ 的坐标；

(3)、点 $P$ 在抛物线的对称轴上，点 $Q$ 是抛物线上位于第四象限内的点，当 $△ C P Q$ 为等边三角形时，求直线 $B Q$ 的解析式．

查看试题解析