北京市重点大学附中2023-2024学年八年级上学期开学考试数学试卷
试卷更新日期:2023-09-27 类型:开学考试
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、
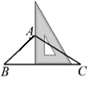 B、
B、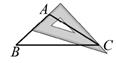 C、
C、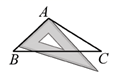 D、
D、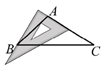 2. 正五边形的外角和为( )A、180° B、360° C、540° D、720°3. 如图,是的平分线, , , 则( )
2. 正五边形的外角和为( )A、180° B、360° C、540° D、720°3. 如图,是的平分线, , , 则( ) A、 B、 C、 D、4. 已知二元一次方程 , 用含的代数式表示 , 正确的是( )A、 B、 C、 D、5. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )
A、 B、 C、 D、4. 已知二元一次方程 , 用含的代数式表示 , 正确的是( )A、 B、 C、 D、5. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )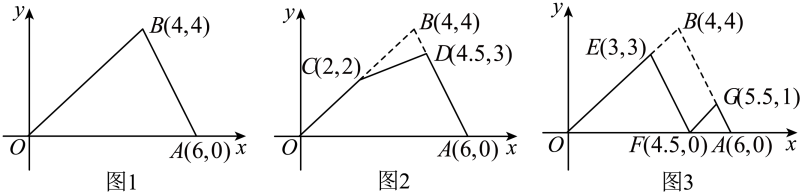 A、 B、且 C、 D、且6. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A、 B、且 C、 D、且6. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )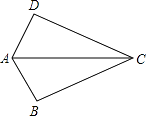 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°7. 年国家统计局公布了年国民经济和社会发展统计公报公报显示了全国年至年货物进出口额的变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图根据统计图提供的信息,下列结论正确的是( )
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°7. 年国家统计局公布了年国民经济和社会发展统计公报公报显示了全国年至年货物进出口额的变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图根据统计图提供的信息,下列结论正确的是( ) 与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升;
与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升;从年到年,进口额最多的是年;
年进口额年增长率持续下降;
与年相比,年出口额增加了万亿元.
A、 B、 C、 D、8. 已知 , 则下列结论正确的是( )A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
9. 已知关于的不等式的解集如图所示,那么的值是 .
 10. 计算: .11. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.12. 已知 , , 则用含的式子表示为 .13. 如图,在中, , , , 平分则的度数为 .
10. 计算: .11. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.12. 已知 , , 则用含的式子表示为 .13. 如图,在中, , , , 平分则的度数为 .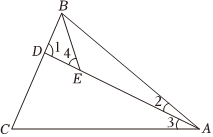 14. 在中, , 点是上一点,将沿翻折后得到 , 边交于点若 , .
14. 在中, , 点是上一点,将沿翻折后得到 , 边交于点若 , . (1)、则的度数为 ;(2)、若中有两个角相等,则 .15. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度.
(1)、则的度数为 ;(2)、若中有两个角相等,则 .15. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度.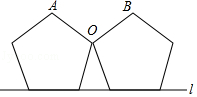 16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.
16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.尺寸
数量个
款式
大
中
小
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.
某批次需要生产个大尺寸陶艺品,个中尺寸陶艺品,个小尺寸陶艺品.
(1)、烧制这批陶艺品,款电热窑至少使用 次;(2)、若款电热窑每次烧制成本为元,款电热窑每次烧制成本为元,则烧制这批陶艺品成本最低为 元三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:(1)、解不等式组:;(2)、已知方程 , 当时 , 当时 , 求和的值.18. 已知如图所示,
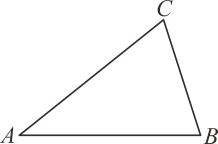 (1)、画出中边上的高线 , 在内部作射线使得 , 交边于点 , 请你依题意补全图形;(2)、判断与之间的关系,并说明理由.19. 如图,点 , , , 在直线上之间不能直接测量 , 点 , 在异侧,测得 , , 求证: .
(1)、画出中边上的高线 , 在内部作射线使得 , 交边于点 , 请你依题意补全图形;(2)、判断与之间的关系,并说明理由.19. 如图,点 , , , 在直线上之间不能直接测量 , 点 , 在异侧,测得 , , 求证: . 20. 在平面直角坐标系中,的三个顶点分别是 , , .(1)、在所给的图中,画出这个平面直角坐标系;(2)、点经过平移后对应点为 , 将作同样的平移得到 , 画出平移后的;(3)、在(2)的条件下,点在直线上,若 , 直接写出点的坐标;(4)、在(2)的条件下,已知 , 点 , 点 , 所围成的区域内包括边界恰有个整点,求的取值范围.
20. 在平面直角坐标系中,的三个顶点分别是 , , .(1)、在所给的图中,画出这个平面直角坐标系;(2)、点经过平移后对应点为 , 将作同样的平移得到 , 画出平移后的;(3)、在(2)的条件下,点在直线上,若 , 直接写出点的坐标;(4)、在(2)的条件下,已知 , 点 , 点 , 所围成的区域内包括边界恰有个整点,求的取值范围.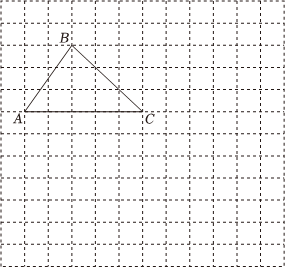 21. 如图,中, , , E点为射线上一动点,连结 , 作且 .
21. 如图,中, , , E点为射线上一动点,连结 , 作且 . (1)、如图1,过F点作交于D点,求证:;(2)、如图2,连结交于G点,若 , , 求证:E点为中点.(3)、当E点在射线上,连结与直线交于G点,若 , , 则 . (直接写出结果)22. 已知点和图形 , 为图形上一点,若存在点 , 使得点为线段的中点不重合 , 则称点为图形关于点的倍点.
(1)、如图1,过F点作交于D点,求证:;(2)、如图2,连结交于G点,若 , , 求证:E点为中点.(3)、当E点在射线上,连结与直线交于G点,若 , , 则 . (直接写出结果)22. 已知点和图形 , 为图形上一点,若存在点 , 使得点为线段的中点不重合 , 则称点为图形关于点的倍点.如图,在平面直角坐标系中,点 , , , .
 (1)、若点的坐标为 , 则在 , , 中,是正方形关于点的倍点的是 ;(2)、点的坐标为 , 若在第一三象限的角平分线才存在正方形关于点的倍点,求的取值范围;(3)、已知点 , , 若线段上的所有点均可成为正方形关于其边上某一点的倍点,直接写出点的取值范围.
(1)、若点的坐标为 , 则在 , , 中,是正方形关于点的倍点的是 ;(2)、点的坐标为 , 若在第一三象限的角平分线才存在正方形关于点的倍点,求的取值范围;(3)、已知点 , , 若线段上的所有点均可成为正方形关于其边上某一点的倍点,直接写出点的取值范围.