安徽省合肥四十六中九年级上学期开学考数学试卷

试卷更新日期：2023-09-27 类型：开学考试

进入出卷网下载

一、选择题（共10小题，每小题4分，满分40分）

1. 下列各数中，与 $\sqrt{3}$ 是同类二次根式的是（　　）

A、 $\sqrt{50}$ B、 $\sqrt{24}$ C、 $\sqrt{27}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 用配方法解下列方程时，配方错误的是（）

A、 $x^{2} + 2 x - 99 = 0$ 化为 ${(x + 1)}^{2} = 100$ B、 $2 x^{2} - 7 x - 4 = 0$ 化为 ${(x - \frac{7}{4})}^{2} = \frac{81}{16}$ C、 $x^{2} + 8 x + 9 = 0$ 化为 ${(x + 4)}^{2} = 25$ D、 $3 x^{2} - 4 x - 2 = 0$ 化为 ${(x - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
3. 某企业今年1月份产值为 $a$ 万元，2月份比1月份减少了10%，3月份又开始了回暖，已知3，4月份平均月增长率为10%，则4月份的产值是（）

A、 $(a - 10 %) (a + 20 %)$ 万元 B、 $a (1 - 10 %) {(1 + 10 %)}^{2}$ 万元 C、 $a (1 - 10 %) (1 + 20 %)$ 万元 D、 $a (1 + 10 %)$ 万元

查看试题解析
4. 定义：如果一元二次方程ax²+bx+c=0（a≠0）满足a+b+c=0，那么我们称这个方程为“凤凰”方程．已知ax²+bx+c=0（a≠0）是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是（）

A、a=c B、a=b C、b=c D、a=b=c

查看试题解析
5. 如图，在△ABC中，点E，D，F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四个判断中，不正确的是（　　）

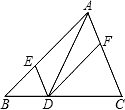A、四边形AEDF是平行四边形 B、如果∠BAC=90°，那么四边形AEDF是矩形 C、如果AD平分∠BAC，那么四边形AEDF是菱形 D、如果AD⊥BC且AB=AC，那么四边形AEDF是正方形

查看试题解析
6. 如图，任意四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，对于四边形EFGH的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（　　）

A、当E，F，G，H是各边中点，且AC＝BD时，四边形EFGH为菱形 B、当E，F，G，H是各边中点，且AC⊥BD时，四边形EFGH为矩形 C、当E，F，G，H不是各边中点时，四边形EFGH可以为平行四边形 D、当E，F，G，H不是各边中点时，四边形EFGH不可能为菱形

查看试题解析
7. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝5，F为DE的中点.若△CEF的周长为18，则OF的长为（　　）

A、3 B、4 C、 $\frac{5}{2}$ D、 $\frac{7}{2}$

查看试题解析
8. 为了了解班上体育锻炼情况，班主任从八（1）班45名同学中随机抽取了8位同学开展“1分钟跳绳”测试，得分如下（满分10分）：10，6，9，9，7，8，9，6，则以下判断正确的是（）

A、这组数据的众数是9，说明全班同学的平均成绩达到9分 B、这组数据的方差是2，说明这组数据的波动很小 C、这组数据的中位数是8，说明8分以上的人数占大多数 D、这组数据的平均数是8，可以估计班上其他同学的平均成绩大约也是8分

查看试题解析
9. 对于函数 $y = {(x + 2)}^{2} - 9$ ，下列结论错误的是（）

A、图象顶点是 $(- 2 ， - 9)$ B、图象开口向上 C、图象关于直线 $x = - 2$ 对称 D、函数最大值为-9

查看试题解析
10. 如图，在菱形ABCD中， $A B = 4$ ， E是AB边上一点，且 $∠ A = ∠ E D F = 60 °$ ，有下列结论：
① $△ D E F$ 是等边三角形；② $∠ A D E = ∠ B E F$ ；③ $△ B E F$ 周长的最小值为 $4 + 2 \sqrt{3}$ ；④ $△ B E F$ 面积的最大值为 $\sqrt{3}$ .

其中正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分.）

11. 有一组数据：5，2， $a$ ， 5，2，6，它们的中位数是4.5，则这组数据的方差是.

查看试题解析
12. 若m、n是方程 $x^{2} + x - 1 = 0$ 的两不同的根，则 $m^{3} + m^{2} + n$ 的值为.

查看试题解析
13. 某抛物线的顶点为（3，-4），并且经过点（4，-2），则此抛物线的解析式为.

查看试题解析
14. 如图，直角边分别为3，4的两个直角三角形如图摆放，M，N为斜边的中点，则线段MN的长为．

查看试题解析
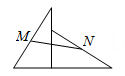15. 在某张三角形纸片上，取其一边的中点，沿着过这点的两条中位线分别剪去两个三角形，剩下的部分就是如图所示的四边形；经测量这个四边形的相邻两边长为10cm、6cm，一条对角线的长为8cm；则原三角形纸片的周长是.

查看试题解析
16. 如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是.

查看试题解析

三、解答题

17. 计算： $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{24} \div \sqrt{3}$

查看试题解析
18. 解方程： $x (x - 4) = 5$ ．

查看试题解析
19. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D、E分别是边AB、AC的中点，延长DE至F ，使得 $A F ∥ C D$ ，连接BF、CF.

(1)、求证：四边形AFCD是菱形；

(2)、当 $A C = 4$ ， $B C = 3$ 时，求BF的长.

查看试题解析
20. 如图，一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ．求：

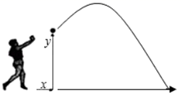(1)、铅球在行进中的最大高度；

(2)、该男生将铅球推出的距离是多少m？

查看试题解析
21. 某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元.为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施.经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.求：

(1)、若商场平均每天要赢利1200元，每件衬衫应降价多少元？

(2)、要使商场平均每天赢利最多，请你帮助设计方案.

查看试题解析
22. 已知正方形ABCD ，点E在AB上，点G在AD ，点F在射线BC上，点H在CD上.

(1)、如图1， $D E ⊥ F G$ ，求证： $B F = A E + A G$ ；

(2)、如图2， $D E ⊥ D F$ ， P为EF中点，求证： $B E = \sqrt{2} P C$ ；

(3)、如图3，EH交FG于O ， $∠ G O H = 45 °$ ，若 $C D = 4$ ， $B F = D G = 1$ ，则线段EH的长为.

查看试题解析