湖南省长沙省明德教育集团2022—2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 下列数中,是无理数的是( )A、 B、 C、 D、2. 已知三角形两边的长分别是2和5,则此三角形第三边的长可能是( )A、1 B、2 C、3 D、43. 若 , 则下列结论一定成立的是( )A、 B、 C、 D、4. 我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥中的斜拉索桥,那么你能推断出斜拉索大桥中运用的数学原理是( )
 A、三角形的不稳定性 B、三角形的稳定性 C、四边形的不稳定性 D、四边形的稳定性5. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一条直线的两条直线平行 B、三角形一个外角大于它的任何一个内角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行6. 将一副三角板()按如图所示方式摆放,使得 , 则等于( )
A、三角形的不稳定性 B、三角形的稳定性 C、四边形的不稳定性 D、四边形的稳定性5. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一条直线的两条直线平行 B、三角形一个外角大于它的任何一个内角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行6. 将一副三角板()按如图所示方式摆放,使得 , 则等于( )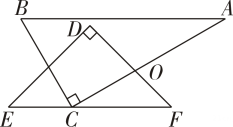 A、 B、 C、 D、7. 黄金分割数是一个很奇妙的数,它大量应用于艺术、建筑和统计决策等方面.请你估算黄金分割数的分子-1的值所在的范围是( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间8. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )A、 B、 C、 D、9. 如图,是的中线, , 的周长与的周长差为( )
A、 B、 C、 D、7. 黄金分割数是一个很奇妙的数,它大量应用于艺术、建筑和统计决策等方面.请你估算黄金分割数的分子-1的值所在的范围是( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间8. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )A、 B、 C、 D、9. 如图,是的中线, , 的周长与的周长差为( )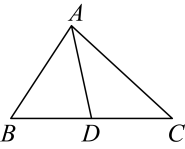 A、2 B、 C、 D、不确定10. 已知直角三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点D从点A到点B沿AB运动,CD=x , 则x的取值范围是( ) .
A、2 B、 C、 D、不确定10. 已知直角三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点D从点A到点B沿AB运动,CD=x , 则x的取值范围是( ) .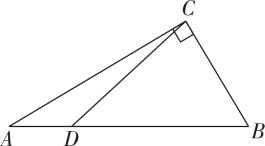 A、 ≤x≤3 B、 ≤x<4 C、 ≤x≤4 D、 ≤x≤5
A、 ≤x≤3 B、 ≤x<4 C、 ≤x≤4 D、 ≤x≤5二、填空题
-
11. 比较大小: .12. 36的平方根是.13. 若七边形的内角中有一个角为 , 则其余六个内角之和为 .14. 直线交于点O , , , 则 .
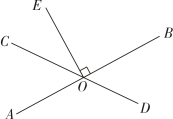 15. 在平面直角坐标系中,已知线段轴,且 , 点的坐标是 , 则点的坐标为 .16. 已知关于x的不等式组 的整数解仅有4个,则a的取值范围是 .
15. 在平面直角坐标系中,已知线段轴,且 , 点的坐标是 , 则点的坐标为 .16. 已知关于x的不等式组 的整数解仅有4个,则a的取值范围是 .三、解答题
-
17. 计算:18. 解不等式组 , 并把解集表示在数轴上.
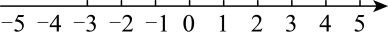 19. 解方程组 .20. 如图,在平面直角坐标系中,点、、的坐标分别为( , ),(4,3),( , 2).将先向左平移4个单位,再向下平移2个单位得到 .
19. 解方程组 .20. 如图,在平面直角坐标系中,点、、的坐标分别为( , ),(4,3),( , 2).将先向左平移4个单位,再向下平移2个单位得到 .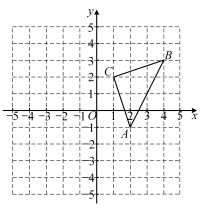 (1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;( ▲ , ▲ )( ▲ , ▲ )( ▲ , ▲ )(3)、求的面积.21. 劳动教育具有树德、增智、强体、育美的综合育人价值,有利于树立正确的劳动价值观为了培养大家的劳动习惯与劳动能力,某校学生发展中心在暑假期间开展了“家务劳动我最行”的实践活动,开学后从本校七至九年级各随机抽取名学生,对他们的每日平均家务劳动时长(单位:)进行了调查,并对数据进行了收集、整理和描述.下面是其中的部分信息:
(1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;( ▲ , ▲ )( ▲ , ▲ )( ▲ , ▲ )(3)、求的面积.21. 劳动教育具有树德、增智、强体、育美的综合育人价值,有利于树立正确的劳动价值观为了培养大家的劳动习惯与劳动能力,某校学生发展中心在暑假期间开展了“家务劳动我最行”的实践活动,开学后从本校七至九年级各随机抽取名学生,对他们的每日平均家务劳动时长(单位:)进行了调查,并对数据进行了收集、整理和描述.下面是其中的部分信息:名学生每日平均家务劳动时长频数分布表
分组
合计
频数
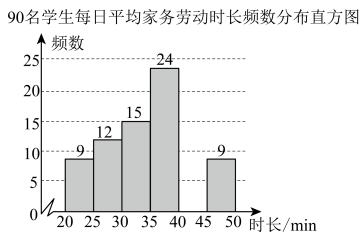
根据以上信息,回答下列问题:
(1)、频数分布表中的组距是 ▲ , ▲ ;(2)、求出频数分布表中的值并补全频数分布直方图;(3)、学生发展中心准备将每日平均家务劳动时长不少于的学生评为“家务小能手”,如果该校七至九年级共有名学生,请估计获奖的学生人数.22. 如图,已知点E、F在直线上,点G在线段上,与交于点H , , .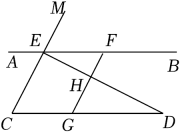 (1)、求证:;(2)、若 , 求的度数.23. 中医药是中华民族的宝贵财富.为更好地弘扬中医药传统文化,传播中医药知识,增进青少年对中华优秀传统文化的了解与认知.明德麓谷学校开展“中草药种植进校园 传承中医药文化”活动,特开设中草药种植课程,计划购买甲、乙两种中草药种子,经过调查得知:每斤甲种种子的价格比每斤乙种种子的价格贵40元,买5斤甲种种子和10斤乙种种子共用1100元.(1)、求每斤甲、乙种子的价格分别是多少元?(2)、若学校需购进乙种中草药种子m斤(其中m为整数),且甲、乙两种中草药种子共120斤,总费用低于8500元,并且要求购进乙种的数量必须不超过甲种数量的3倍,问有几种购买方案?最低费用是多少?24. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②“包含”,其中不等式(组)①与不等式(组)②均有解.
(1)、求证:;(2)、若 , 求的度数.23. 中医药是中华民族的宝贵财富.为更好地弘扬中医药传统文化,传播中医药知识,增进青少年对中华优秀传统文化的了解与认知.明德麓谷学校开展“中草药种植进校园 传承中医药文化”活动,特开设中草药种植课程,计划购买甲、乙两种中草药种子,经过调查得知:每斤甲种种子的价格比每斤乙种种子的价格贵40元,买5斤甲种种子和10斤乙种种子共用1100元.(1)、求每斤甲、乙种子的价格分别是多少元?(2)、若学校需购进乙种中草药种子m斤(其中m为整数),且甲、乙两种中草药种子共120斤,总费用低于8500元,并且要求购进乙种的数量必须不超过甲种数量的3倍,问有几种购买方案?最低费用是多少?24. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②“包含”,其中不等式(组)①与不等式(组)②均有解.例如:不等式被不等式“包含”.
(1)、下列不等式(组)中,能被不等式“包含”的是____.A、 B、 C、 D、(2)、若关于x的不等式被“包含”,若且 , 求M的最小值.(3)、已知 , , 且k为整数,关于x的不等式P: , Q: , 请分析是否存在k , 使得P和Q存在“包含”关系,且Q被P“包含”,若存在,请求出k的值,若不存在,请说明理由.25. 已知 , , 满足 , C , D分别为x轴,y轴正半轴上的点,且满足 .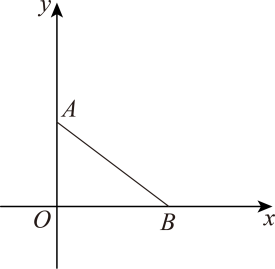
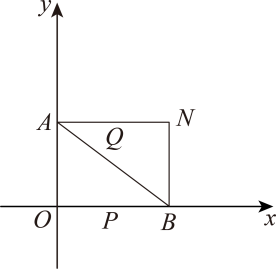
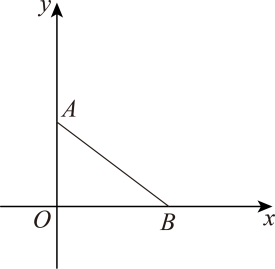 (1)、求A , B两点的坐标.(2)、作和的角平分线交于点M , 试求的比值.(3)、分别过点A、点B作x、y轴的平行线交于点N , 有一动点P从B点出发沿方向以每秒1个单位长度的速度运动,同时有一动点Q从A点出发沿方向以每秒个单位长度的速度运动,当两个点有一个到达终点时另一个随之停止运动,设运动时间为t , 求t为何值时,以P、A、Q、B为顶点的图形的面积为四边形面积的一半?
(1)、求A , B两点的坐标.(2)、作和的角平分线交于点M , 试求的比值.(3)、分别过点A、点B作x、y轴的平行线交于点N , 有一动点P从B点出发沿方向以每秒1个单位长度的速度运动,同时有一动点Q从A点出发沿方向以每秒个单位长度的速度运动,当两个点有一个到达终点时另一个随之停止运动,设运动时间为t , 求t为何值时,以P、A、Q、B为顶点的图形的面积为四边形面积的一半?