湖南省长沙市浏阳市2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 下列各点中,位于第二象限的是( )A、 B、 C、 D、3. 不等式3x-1<x+3的解集在数轴上表示正确的是( )A、
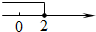 B、
B、 C、
C、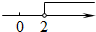 D、
D、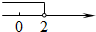 4. 在世界无烟日(月日),小华为了了解所住小区大约有多少成年人在吸烟,随机调查了个成年人,结果其中有个成年人吸烟.对于这个数据收集与处理的问题,下列说法正确的是( )A、调查的方式是普查 B、所住小区只有个成年人不吸烟 C、样本容量是 D、样本容量是5. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、
4. 在世界无烟日(月日),小华为了了解所住小区大约有多少成年人在吸烟,随机调查了个成年人,结果其中有个成年人吸烟.对于这个数据收集与处理的问题,下列说法正确的是( )A、调查的方式是普查 B、所住小区只有个成年人不吸烟 C、样本容量是 D、样本容量是5. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、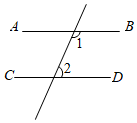 B、
B、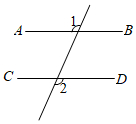 C、
C、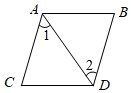 D、
D、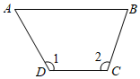 6. 一个正方体的体积扩大为原来的倍,则它的棱长为原来的( )A、倍 B、倍 C、倍 D、倍7. 如果3xm+n+5ym﹣n﹣2=0是一个关于x、y 的二元一次方程,那么( )A、 B、 C、 D、8. 一个两位数的两个数字之和为10,两个数字之差为6,求这个两位数,此题的解有( )A、0个 B、1个 C、2个 D、4个9. 如图,将直角三角形ABC沿AB方向平移2cm得到 , DF交BC于点H , , , 则阴影部分的面积为( )
6. 一个正方体的体积扩大为原来的倍,则它的棱长为原来的( )A、倍 B、倍 C、倍 D、倍7. 如果3xm+n+5ym﹣n﹣2=0是一个关于x、y 的二元一次方程,那么( )A、 B、 C、 D、8. 一个两位数的两个数字之和为10,两个数字之差为6,求这个两位数,此题的解有( )A、0个 B、1个 C、2个 D、4个9. 如图,将直角三角形ABC沿AB方向平移2cm得到 , DF交BC于点H , , , 则阴影部分的面积为( )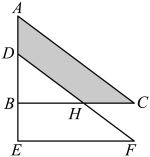 A、6cm2 B、8cm2 C、12cm2 D、16cm210. 已知关于x的不等式(1-a)x>3的解集为x< , 则a的取值范围是( )A、a>0 B、a>1 C、a<0 D、a<1
A、6cm2 B、8cm2 C、12cm2 D、16cm210. 已知关于x的不等式(1-a)x>3的解集为x< , 则a的取值范围是( )A、a>0 B、a>1 C、a<0 D、a<1二、填空题
-
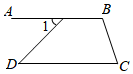
11. 若有意义,请写出符合条件的一个x的值: .12. 已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 .13. 如图,若∠1=∠D , ∠C=76°,则∠B= .
 14. 有P、Q、R、S四个人去公园玩跷跷板,依据下面的示意图,则这四个人中最重的是 .
14. 有P、Q、R、S四个人去公园玩跷跷板,依据下面的示意图,则这四个人中最重的是 .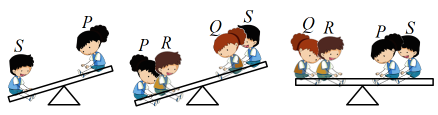 15. 对于非零实数 , 规定.若 , 则x的值为.16. 一道来自课本的习题:
15. 对于非零实数 , 规定.若 , 则x的值为.16. 一道来自课本的习题:从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x , y , 已经列出一个方程 , 则另一个方程是 .
三、解答题
-
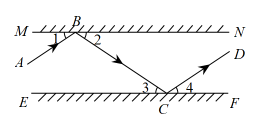
17. 计算:18. 解方程组:19. 如图, , 分别表示两个互相平行的镜面,一束光线照射到镜面上,反射光线为 , 此时;光线经过镜面反射后的光线为 , 此时 . 试判断与的位置关系,并说明理由.
答: .
理由:延长射线交于点 .
.
▲ ( )
, (已知)
▲ (等量代换)
又 ,
( )
▲ (等量代换)
( )
20. 解不等式组 , 并把解集在数轴上表示出来.21. 在边长为的正方形网格中建立平面直角坐标系,位置如图.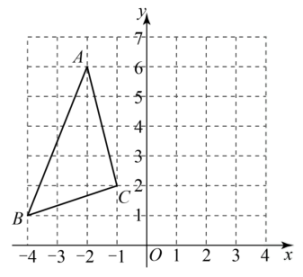 (1)、请写出 , , 三点的坐标;(2)、将向右平移个单位长度,再向上平移个单位长度得到 , 请在图中作出平移后的三角形,并写出点的坐标;(3)、求出的面积.22. 为有效推进儿童青少年近视防控工作,教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-025年)》,共提出八项主要任务,其中第三项任务为强化户外活动和体育锻炼.我市各校积极落实方案精神,某学校决定开设以下四种球类的户外体育选修课程篮球、足球、排球、乒乓球.为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成如下不完整的统计图表.
(1)、请写出 , , 三点的坐标;(2)、将向右平移个单位长度,再向上平移个单位长度得到 , 请在图中作出平移后的三角形,并写出点的坐标;(3)、求出的面积.22. 为有效推进儿童青少年近视防控工作,教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案(2021-025年)》,共提出八项主要任务,其中第三项任务为强化户外活动和体育锻炼.我市各校积极落实方案精神,某学校决定开设以下四种球类的户外体育选修课程篮球、足球、排球、乒乓球.为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成如下不完整的统计图表.课程
人数
篮球
m
足球
21
排球
30
乒乓球
n

根据图表信息,解答下列问题:
(1)、分别求出表中m , n的值;(2)、求扇形统计图中“足球”对应的扇形圆心角的度数;(3)、该校共有2000名学生,请你估计其中选择“乒乓球”课程的学生人数.23. 2022年北京冬奥会的吉祥物冰墩墩和雪容融相关的商品,很受孩子们喜欢,其中最受欢迎的是冰墩墩立体钥匙扣和雪容融吉样徽章.某官方授权的专卖店销售这两种商品的价格如图.问: (1)、已知该专卖店某天共卖出这两种商品1000件,共获得销售额76000元.求该网店这天售出冰墩墩立体钥匙扣和雪容融吉祥徽章分别是多少件?(2)、某学校准备购买冰墩墩立体钥匙扣和雪容融吉祥徽章共100个用于奖品发放,但总金额不得超过8000元,问最多可购买雪容融吉祥徽章多少个?24.
(1)、已知该专卖店某天共卖出这两种商品1000件,共获得销售额76000元.求该网店这天售出冰墩墩立体钥匙扣和雪容融吉祥徽章分别是多少件?(2)、某学校准备购买冰墩墩立体钥匙扣和雪容融吉祥徽章共100个用于奖品发放,但总金额不得超过8000元,问最多可购买雪容融吉祥徽章多少个?24. (1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.25. 在平面直角坐标系中,对于任意三点A , B , C的“矩面积”,给出如下定义:“水平底”a:任何两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积” .
(1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.25. 在平面直角坐标系中,对于任意三点A , B , C的“矩面积”,给出如下定义:“水平底”a:任何两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积” .例如:三点坐标分别为 , , , 则“水平底” , “铅垂高” , “矩面积” .
(1)、已知点 , , , 求三点的“矩面积”S .(2)、若点 , , 三点的“矩面积”S为12,求点P的坐标.