四川省成都市温江区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 以下分别是回收、节水、绿色包装、低碳4个标志,其中是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、对角线相等且垂直的四边形是正方形 B、对角线相等且互相平分的四边形是菱形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线相等的平行四边形是矩形3. 在下列不等式中,解集为的是( )A、 B、 C、 D、4. 下列分解因式正确的是( )A、 B、 C、 D、5. 如果一个多边形的内角和等于其外角和的2倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 如图,F是正方形对角线上一点,连接 , , 并延长交于点E.若 , 则的度数为( )
2. 下列说法正确的是( )A、对角线相等且垂直的四边形是正方形 B、对角线相等且互相平分的四边形是菱形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线相等的平行四边形是矩形3. 在下列不等式中,解集为的是( )A、 B、 C、 D、4. 下列分解因式正确的是( )A、 B、 C、 D、5. 如果一个多边形的内角和等于其外角和的2倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 如图,F是正方形对角线上一点,连接 , , 并延长交于点E.若 , 则的度数为( ) A、 B、 C、 D、7. 某车间加工600个零件后采用了新工艺,工效提高了50%,这样加工同样多的零件少用5h,求采用新工艺前、后每小时分别加工多少个零件?若设采用新工艺前每小时加工x个零件,则可列方程为( )A、 B、 C、 D、8. 如图,已知的顶点 , , 点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点M,作射线交于点G.则点G的坐标为( )
A、 B、 C、 D、7. 某车间加工600个零件后采用了新工艺,工效提高了50%,这样加工同样多的零件少用5h,求采用新工艺前、后每小时分别加工多少个零件?若设采用新工艺前每小时加工x个零件,则可列方程为( )A、 B、 C、 D、8. 如图,已知的顶点 , , 点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点M,作射线交于点G.则点G的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 因式分解: .10. 如图,将沿向右平移得到 , 若 , , 则 .
 11. 如图,在平面直角坐标系中,函数与的图象交于点 , 则不等式的解集为 .
11. 如图,在平面直角坐标系中,函数与的图象交于点 , 则不等式的解集为 . 12. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点E和F;②作直线交于点P.若 , , . 则的长为 .
12. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点E和F;②作直线交于点P.若 , , . 则的长为 .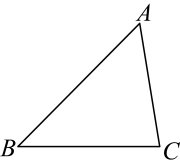 13. 如图,边长为的等边三角形中,是对称轴上的一个动点,连接将线段绕点顺时针旋转得到 , 连接 , 则在点运动过程中,的最小值是 .
13. 如图,边长为的等边三角形中,是对称轴上的一个动点,连接将线段绕点顺时针旋转得到 , 连接 , 则在点运动过程中,的最小值是 .
三、解答题
-
14.(1)、分解因式: .(2)、解不等式组 , 并在数轴上表示出解集.15. 解方程: .16. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 .
 (1)、平移 , 使得点A的对应点的坐标为 , 画出平移后的 .(2)、将绕点O旋转 , 画出旋转后的 .(3)、若与Δ关于点P成中心对称,求点P的坐标.17. 先化简,再求值: , 然后从 , 0,1,3中选一个合适的数作为x的值代入求值.18. 如图,四边形是矩形,点E,F分别在边 , 上,将矩形沿对折,点B与点D恰好重合.
(1)、平移 , 使得点A的对应点的坐标为 , 画出平移后的 .(2)、将绕点O旋转 , 画出旋转后的 .(3)、若与Δ关于点P成中心对称,求点P的坐标.17. 先化简,再求值: , 然后从 , 0,1,3中选一个合适的数作为x的值代入求值.18. 如图,四边形是矩形,点E,F分别在边 , 上,将矩形沿对折,点B与点D恰好重合. (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.四、填空题
-
19. 若 , 则的值为 .20. 以正六边形的顶点D为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线CD上,则正六边形ABCDEF至少旋转 °.
 21. 如图,中,对角线、相交于点O,交于点E,已知的周长为12,则的周长为 .
21. 如图,中,对角线、相交于点O,交于点E,已知的周长为12,则的周长为 . 22. 若关于x的方程的解是正数,则a的取值范围是 .23. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为4,是它的较短对角线,点E,F分别是边 , 上的两个动点,且 , 点G为的中点,点P为边上的动点,则的最小值为 .
22. 若关于x的方程的解是正数,则a的取值范围是 .23. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为4,是它的较短对角线,点E,F分别是边 , 上的两个动点,且 , 点G为的中点,点P为边上的动点,则的最小值为 .
五、解答题
-
24. 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行.大动会场馆共计49个,包括13个新建场馆和36个改造场馆.现计划对面积为的某场馆区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为区域的绿化时,甲队比乙队少用2天.(1)、求甲、乙两工程队每天能完成绿化的面积;(2)、设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;(3)、在(2)的条件下,若甲队每天绿化费用是2万元,乙队每天绿化费用为0.8万元,且甲乙两队施工的总天数不超过20天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.

