四川省成都市双流区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 火锅,是四川人的家常便饭,也是外地人来四川必吃的美食,无辣不欢,无火锅不四川.下面是四种火锅的设计图,其中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 两边都除以 , 得( )A、 B、 C、 D、3. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 如图,平面直角坐标系中,线段的两端点坐标分别为 , , 现将该线段沿轴向右平移,使得点与原点重合,得到线段 , 则点的坐标是( )
2. 若 , 两边都除以 , 得( )A、 B、 C、 D、3. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 如图,平面直角坐标系中,线段的两端点坐标分别为 , , 现将该线段沿轴向右平移,使得点与原点重合,得到线段 , 则点的坐标是( )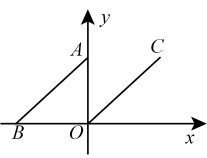 A、 B、 C、 D、5. 如图,在中, , , 边的垂直平分线分别交 , 于 , 两点,则的周长为( )
A、 B、 C、 D、5. 如图,在中, , , 边的垂直平分线分别交 , 于 , 两点,则的周长为( )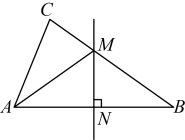 A、 B、 C、 D、6. 如图,一束太阳光线平行照射在放置于地面的正五边形上,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,一束太阳光线平行照射在放置于地面的正五边形上,若 , 则的度数为( ) A、 B、 C、 D、7. 若关于的分式方程有增根,则增根为( )A、 B、 C、 D、8. 如图,在中, , 为边上的高,为边上的中线,若的面积为 , , 则的长度为( )
A、 B、 C、 D、7. 若关于的分式方程有增根,则增根为( )A、 B、 C、 D、8. 如图,在中, , 为边上的高,为边上的中线,若的面积为 , , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 分式 在实数范围内有意义,则x的取值范围是 .10. 小明为测量一卷粗细均匀的电线的长度,他先从这卷电线上取米长的电线,称它的质量为克,再称得剩余电线的质量为克,那么剩余电线的长度是米.11. 如图,在中,是对角线上的点, , , 则的大小为 .
 12. 如图,在△ABC中,AB=AC,∠A=40°,BD⊥AC于D,则∠DBC=度.
12. 如图,在△ABC中,AB=AC,∠A=40°,BD⊥AC于D,则∠DBC=度. 13. 已知一次函数y=kx+b的图象如图,则关于x的不等式kx+b>0的解集是 .
13. 已知一次函数y=kx+b的图象如图,则关于x的不等式kx+b>0的解集是 .
三、解答题
-
14. 计算(1)、因式分解:;(2)、解不等式组 .15. 先化简,再求值: , 其中 .16. 如图,在四边形中, , 的平分线交的延长线于点 , 交于点 , 且 .
 (1)、求证:四边形是平行四边形;(2)、若 , , , 求四边形的面积.17. 《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为,一段高速公路全程限速千米/时(即每一时刻的车速都不能超过千米/时),以下是张师傅和李师傅行驶完这段全程为千米的高速公路时的对话片段,张:“你的车速太快了,平均每小时比我多跑 , 少用我一个小时就跑完了全程,还是慢点.”李:“虽然我的时速快,但最快时速比我的平均时速只快 , 可没有超速违法啊,”李师傅超速违法吗?为什么?18. 如图,中, , 点沿方向从点开始以每秒个单位长度的速度运动,过点的直线与平行,分别与射线 , , 交于点 , , , 设运动时间为秒.
(1)、求证:四边形是平行四边形;(2)、若 , , , 求四边形的面积.17. 《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为,一段高速公路全程限速千米/时(即每一时刻的车速都不能超过千米/时),以下是张师傅和李师傅行驶完这段全程为千米的高速公路时的对话片段,张:“你的车速太快了,平均每小时比我多跑 , 少用我一个小时就跑完了全程,还是慢点.”李:“虽然我的时速快,但最快时速比我的平均时速只快 , 可没有超速违法啊,”李师傅超速违法吗?为什么?18. 如图,中, , 点沿方向从点开始以每秒个单位长度的速度运动,过点的直线与平行,分别与射线 , , 交于点 , , , 设运动时间为秒. (1)、求证:;(2)、当四边形的面积与的面积相等时,求的值.
(1)、求证:;(2)、当四边形的面积与的面积相等时,求的值.四、填空题
-
19. 已知非零实数 , 满足 , 则的值等于 .20. 如图,在中, , , , , 分别为 , 上的中点,连接 , , 分别取 , , 的中点 , , , 顺次连接 , , , 则的周长为 .
 21. 如图,在中, , 于 , 点在上,在内部,且 , 交于 , 若 , , 则的长为(用含 , 的代数式表示).
21. 如图,在中, , 于 , 点在上,在内部,且 , 交于 , 若 , , 则的长为(用含 , 的代数式表示). 22. 若整数既能使关于的不等式组有解,也能使关于的分式方程有整数解,则整数的值为 .23. 如图,正方形的边长为 , 点是边上的一动点,连接 , 将绕点顺时针方旋转后得到 , 连接 , 则点在整个运动过程中,线段所扫过的图形面积为 .
22. 若整数既能使关于的不等式组有解,也能使关于的分式方程有整数解,则整数的值为 .23. 如图,正方形的边长为 , 点是边上的一动点,连接 , 将绕点顺时针方旋转后得到 , 连接 , 则点在整个运动过程中,线段所扫过的图形面积为 .
五、解答题
-
24. 为了市民游玩方便,准备在风阳湖市政森林公国内的环形路上提供免费游览车服务,如图是游览车路线图,已知间的路程为米,间的路程为米,间的路程为米,间的路程为米,现有有号,号两游览车分别从出口A和景点同时出发,号车逆时针、号车顺时针沿环形路连续循环行驶,供游客随时免费乘车(上,下车的时间忽略不计),两车速度均为米/分.
 (1)、探究:设行驶时间为分.
(1)、探究:设行驶时间为分.①当时,分别写出号车,号车在下半圈环线离出口A的路程 , (米)与(分)的函数关系式,并求出当两车相距的路程少于米时的取值范围;
②为何值时,号车第三次恰好经过景点 , 并直接写出这一段时间内它与号车相遇过的次数.
(2)、应用:已知游客小双在上从景点向出口A走去,步行的速度是米/分,当行进到上一点(不与点 , A重合)时,刚好与号车迎面相遇,设的路程为s米,写出他原地等候乘号车到出口A所花时间与的函数关系式,并直接写出在什么范围内时,等候乘号车能更快到达.25. 综合与实践:问题情境:数学课上,小广和小都两位同学利用三角板操作探究图形的旋转问题.
 (1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.
(1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.其中两个角顶点重合于点 , 与重合,已知长 , 请你帮小都同学求出此时点、之间的距离;
(3)、操作探究:随后,小将图②中的换成了含角的三角板,同相是顶点重合于点 , 与重合,已知直角边与长均为 , 他还想求点 , 之间距离,小广提出,如果把三角板也换成了含角的三角板,并利用旋转的知识,结论将更容易得到,你能求出此时点 , 之间的距离吗?26. 如图①,平面直角坐标系中,直线与轴,轴分别交于点 , , 直线 , 交轴于点 , 点位于点右侧的轴上,且 , 点在轴正半轴上,且 , 直线交于点 . (1)、点的横坐标为 , 当点在原点左侧时,;(均用含的代数式表示)(2)、当为等腰三角形时,求的值;(3)、如图②,点是点关于直线的对称点,连接 , , 若四边形为平行四边形,求的值(直接写出答案)
(1)、点的横坐标为 , 当点在原点左侧时,;(均用含的代数式表示)(2)、当为等腰三角形时,求的值;(3)、如图②,点是点关于直线的对称点,连接 , , 若四边形为平行四边形,求的值(直接写出答案)