天津市滨海新区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 25的算术平方根是 $($ $)$

A、 5 B、 $\pm 5$ C、 $- 5$ D、25

查看试题解析
2. 在平面直角坐标系中，下列各点位于第四象限的是（）

A、 $(- 1 ， 6)$ B、 $(- 5 ， - 3)$ C、 $(2 ， - 2)$ D、 $(4 ， 3)$

查看试题解析
3. 估计 $\sqrt{15} + 1$ 的值在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
4. 如图，直线a，b相交， $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $140 °$ B、 $50 °$ C、 $40 °$ D、 $130 °$

查看试题解析
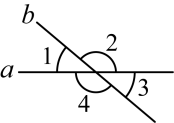5. 如图，在灌溉农田时，要把河 $($ 直线 $l$ 表示一条河 $)$ 中的水引剩农田 $M$ 处，设计了四条路线 $M A$ ， $M B$ ， $M C$ ， $M D ($ 其中 $M C ⊥ l$ $)$ ，要使控渠的路线最短，可以选择的路线为（）

A、 $M A$ B、 $M B$ C、 $M C$ D、 $M D$

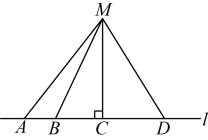查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{{(- 1)}^{2}} = - 1$ B、 $\pm \sqrt{9} = \pm 3$ C、 $- \sqrt{4} = 2$ D、 $\sqrt[3]{- 27} = 3$

查看试题解析
7. 如图，点E在 $A C$ 的延长线上，下列条件中能判断 $B D ∥ A C$ 的是（）

A、 $∠ D + ∠ A C D = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 + ∠ 4 = 180 °$ D、 $∠ A = ∠ D C E$

查看试题解析
8. 下列调查中，最适合采用全面调查方式的是（）

A、了解全市居民身体健康情况 B、对我市中小学生每周课外阅读时间情况的调查 C、了解电视栏目《朗读者》的收视率 D、了解某班学生的视力情况

查看试题解析
9. 如果 $a > b$ ，那么下列不等式中一定成立的是（）

A、 $a - 2 > b + 2$ B、 $3 a < 3 b$ C、 $- a + 1 < - b + 1$ D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
10. 下列命题为真命题的是（）

A、相等的角是对顶角 B、不相交的两条直线是平行线 C、两条直线被第三条直线所截，内错角相等 D、经过直线外一点，有且只有一条直线与这条直线平行

查看试题解析
11. 甲、乙二人从相距22 $k m$ 的两地同时出发相向而行，经过20 $m i n$ 相遇，如果甲的速度比乙的速度每分钟多12 $m$ ，求甲乙二人的速度，设甲、乙的速度分别为x $m / m i n$ ， y $m / m i n$ ，则可列方程组为（）

A、 ${\begin{array}{l} x - y = 12 \\ 20 (x + y) = 22 \end{array}$ B、 ${\begin{array}{l} x - y = 12 \\ 20 (x + y) = 22000 \end{array}$ C、 ${\begin{array}{l} y - x = 12 \\ 20 (x + y) = 22 \end{array}$ D、 ${\begin{array}{l} y - x = 12 \\ 20 (x + y) = 22000 \end{array}$

查看试题解析
12. 关于x的不等式组 ${\begin{array}{l} \frac{x - 1}{3} \leq 1 \\ a - x < 2 \end{array}$ 恰好只有四个整数解，则a的取值范围是（）

A、 $2 \leq a < 3$ B、 $2 \leq a \leq 3$ C、 $a < 3$ D、 $2 < a < 3$

查看试题解析

二、填空题

13. $1 - \sqrt{2}$ 的相反数为．

查看试题解析
14. 如图，直线AB，CD相交于点O，若∠BOD=30°，OE⊥CD，则∠AOE的度数为．

查看试题解析
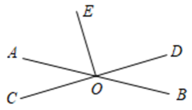15. 若点P $(m + 3 ， m - 1)$ 在 $x$ 轴上，则点P的坐标为.

查看试题解析
16. 一组数据的最大值是 $7.4$ ，最小值是 $4.0$ ，用频数分布直方图描述这一组数据，取组距为 $0.3$ ，则可以分成组．

查看试题解析
17. 若关于x，y的方程 $a x + b y = 2$ 的两个解为 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ 和 ${\begin{array}{l} x = - 1 \\ y = - 7 \end{array}$ ，则 $a + b$ 的值是．

查看试题解析
18. 如图，在平面直角坐标系中，已知点 $A (1 ， 1) ， B (- 1 ， 1) ， C (- 1 ， - 2) ， D (1 ， - 2)$ ，点P，点Q分别从点A，点C同时出发，沿长方形 $A B C D$ 的边作环绕运动，点P按逆时针方向以每秒2个单位长度的速度匀速运动，点Q按顺时针方向以每秒3个单位长度的速度匀速运动，则第2023秒P，Q两点相遇地点的坐标是．

查看试题解析

三、解答题

19. 解方程组：

(1)、 ${\begin{array}{l} y = x - 2 \\ 2 x + 3 y = 9 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x}{4} + \frac{y}{3} = - 1 \\ 5 (x - 8) = 6 (y + 9) \end{array}$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} \frac{11}{3} x + 2 \geq \frac{5}{3} x ， ① \\ 1 - 3 x \geq x - 7 ， ② \end{array}$
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
21. 完成下面的推理，并在括号内标注理由：
如图，已知三角形 $A B C$ 中， $B F ⊥ A C$ 于点 $F$ ，点 $D$ ， $E$ ， $G$ 分别在 $B C$ ， $A C$ ， $A B$ 上，且 $∠ A G F = ∠ A B C$ ， $∠ 1 + ∠ 2 = 180 °$ ．求证： $D E ⊥ A C$ ．

证明： $∵$ $∠ A G F = ∠ A B C$ ，
      $∴$ $G F ∥$     ▲         ．
      $∴ ∠ 1 =$     ▲         ，（  ）
      $∵$ $∠ 1 + ∠ 2 = 180 °$ ，
      $∴$ $∠ 2 +________= 180 °$ $($ 等量代换 $)$ ，
      $∴$ $D E ∥$     ▲         ，（  ）
      $∴ ∠ B F C =$     ▲         ，
      $∵ B F ⊥ A C$ ，
      $∴$ $∠ B F C = 90 °$ $($ 垂直定义 $)$ ，
∴∠    ▲         $= 90 °$ $($ 等量代换 $)$
      $∴ D E ⊥ A C$ ．

查看试题解析
22. 某校动员学生课余时间练习书法，为了了解学生们每天练习书法的情况，该校随机抽取部分学生进行问卷调查，被调查学生在五种选项中选择自己每天练习书法的时间，根据调查结果绘制成如图两幅不完整的统计图，根据统计图提供的信息，解答下列问题：

(1)、本次共调查了名学生；

(2)、在扇形统计图中，m的值是， 20 $m i n$ 所对应的扇形圆心角的度数是度；

(3)、根据以上信息直接在答题卡中补全条形统计图；

(4)、根据以上调查结果，请估计该校800名学生中每天练习书法时间为25 $m i n$ 的学生人数．

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ 交线段 $B C$ 于点 $E$ ， $∠ 1 = ∠ 2$ ， $∠ A = 100 °$ ．求 $∠ B$ 的度数．

查看试题解析
24. 某社区开展“美丽社区”活动，积极推进垃圾分类工作，计划购买 $A$ 、 $B$ 两种类型垃圾桶，已知购买 $2$ 个 $A$ 型垃圾桶的费用与购买 $3$ 个 $B$ 型垃圾桶的费用相同，购买 $14$ 个 $A$ 型垃圾桶和 $4$ 个 $B$ 型垃圾桶共用 $1500$ 元．请解答下列问题：

(1)、求出 $A$ 型垃圾桶和 $B$ 型垃圾桶的单价；

(2)、社区现需一次性购买上述两种类型垃圾桶共 $45$ 个，要求购买的费用不超过 $3400$ 元则最多可购买多少个 $A$ 型垃圾桶？

查看试题解析
25. 在平面直角坐标系中， $O$ 为原点，点 $B$ 的坐标为 $(- 2$ ， $- 6)$ ， $B A ⊥ x$ 轴于点 $A$ ，将线段 $B A$ 沿 $x$ 轴负方向平移 $2 \sqrt{3}$ 个单位长度，平移后得到线段 $C D$ ．在四边形 $A B C D$ 中，点 $P$ 从点 $A$ 出发，沿 $“ A B \to B C \to C D ”$ 方向移动，移动到点 $D$ 停止．若点 $P$ 的速度为每秒 $1$ 个单位长度，设运动时间为 $t$ 秒．

(1)、点 $C$ 的坐标为，线段 $B C$ 与线段 $A D$ 的位置关系是；

(2)、当点 $P$ 在线段 $A B$ 上运动时，若三角形 $A D P$ 的面积为 $3 \sqrt{3}$ ，则此时 $t =$ ；

(3)、当点 $P$ 在线段 $B C$ 上运动时，
①直接写出点 $P$ 在运动过程中的坐标为 ▲ （用含 $t$ 的式子表示）；

②若四边形 $A B P D$ 的面积是四边形 $A B C D$ 面积的 $\frac{2}{3}$ ，求点 $P$ 的横坐标．

查看试题解析