天津市西青区2022-2023学年七年级下学期数学期末试题

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、 $\frac{5}{7}$ B、 $0.1010010001 . . .$ （相邻的两个1之间依次多一个0） C、 $\sqrt[3]{- 8}$ D、 $3 . \dot{7}$

查看试题解析
2. 估计 $\sqrt{31}$ 的值在（）

A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间

查看试题解析
3. 若 $m > n$ ，则下列不等式中正确的是（）

A、 $m + 3 < n + 3$ B、 $m - 5 < n + 2$ C、 $2 m > 2 n$ D、 $- m > - n$

查看试题解析
4. $1.5 - \sqrt{2}$ 的绝对值是（）

A、 $1.5 - \sqrt{2}$ B、 $- 1.5 - \sqrt{2}$ C、 $\sqrt{2} - 1.5$ D、 $1.5 + \sqrt{2}$

查看试题解析
5. 已知点A在第四象限，到x轴的距离是1，到y轴的距离是2，则点A的坐标为（）

A、 $(- 1 ， 2)$ B、 $(- 2 ， 1)$ C、 $(1 ， - 2)$ D、 $(2 ， - 1)$

查看试题解析
6. 下列调查中，适合采用全面调查的是（）

A、对我市食品合格情况的调查 B、对你所在班级同学的身高情况的调查 C、对电视台某栏目收视率的调查 D、对某灯泡厂生产的灯泡使用寿命的调查

查看试题解析
7. 某校组织了第二课堂，分别设置了文艺类，体育类、阅读类、兴趣类四个社团（假设该校要求人人参与社团，每人只能选择一个），为了了解学生喜爱哪种社团活动，学校做了一次抽样调查，并绘制成如图①，图②所示的两幅不完整的统计图，根据图中信息回答，下列结论正确的是（）

A、本次抽样调查的样本容量是50 B、阅读类对应扇形的圆心角是 $90 °$ C、样本中喜爱体育类社团的有16人 D、若全校有800名学生，则喜爱文艺类社团的有200人

查看试题解析
8. 如图，直线 $A B$ ， $E F$ 相交于点 $O$ ，直线 $B C ∥ E F$ ， $O D ⊥ A B$ ，若 $∠ A B C = 50 °$ ，则 $∠ D O E$ 的大小是（）

A、 $40 °$ B、 $50 °$ C、 $90 °$ D、 $130 °$

查看试题解析
9. 下列算式正确的是（）

A、 $\sqrt[3]{64} = 8$ B、 $\sqrt{4} = \pm 2$ C、 $\sqrt{{(- 3)}^{2}} = - 3$ D、 $\pm \sqrt{\frac{169}{225}} = \pm \frac{13}{15}$

查看试题解析
10. 某超市推出一种购物卡，凭卡在该超市购物均可按商品标价的九折优惠，但每张卡收 $100$ 元购卡费，若办理此卡购物比不办卡购物合算，则需按标价累计购物金额超过（）

A、 $1000$ 元 B、 $900$ 元 C、 $800$ 元 D、 $700$ 元

查看试题解析
11. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”若设鸡有x只，免有y只，则下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 35 \\ 2 x + 4 y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ C、 ${\begin{array}{l} x + y = 94 \\ 2 x + 4 y = 94 \end{array}$ D、 ${\begin{array}{l} x + y = 35 \\ x + 4 y = 94 \end{array}$

查看试题解析
12. 下列命题：
①互补的两个角一定是邻补角；②直线外一点到这条直线的垂线段的长度，叫做点到直线的距离；③两直线平行，同旁内角相等；④如果两条直线都与第三条直线平行，那么这两条直线也互相平行；⑤在同一平面内，过一点有且只有一条直线与已知直线垂直．
其中真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. $\sqrt{7} - 3$ 的相反数是．

查看试题解析
14. 如图，这是一个利用平面直角坐标系画出的某学校的示意图，北若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，且综合楼和食堂的坐标分别是 $(4 ， 1)$ 和 $(5 ， 4)$ ，则教学楼的坐标是．

查看试题解析
15. 对某班同学的身高进行统计（单位：厘米），频数分布表中165.5~170.5这一组学生人数是12，频率是0.25，则该班共有名学生

查看试题解析
16. 若式子 $\frac{4 a + 1}{6}$ 表示大于 $- 2$ 的数，则满足条件的所有负整数a的值是．

查看试题解析
17. 如图，将三角形 $A B C$ 沿 $B C$ 方向平移 $2 c m$ 得到三角形 $D E F$ 若三角形 $A B C$ 的周长是 $15 c m$ ，则四边形 $A B F D$ 的周长为 $c m$ ．

查看试题解析
18. 将9个数填入正方形的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，如图①就是填好的一个正方形，图②中已经填好一部分数字．

(1)、图②中是否存在正整数x，y满足上述条件？（填“是”或“否”）．

(2)、若图②中存在正整数x，y满足上述条件，请写出x与y的乘积：若不存在，请说明理由．．

查看试题解析

三、解答题

19. 计算

(1)、解不等式： $3 x + 1 > - x - 3$ ；

(2)、解不等式组 ${\begin{array}{l} 5 x + 1 \geq 3 (x - 1) ① \\ \frac{x - 3}{2} \geq \frac{2 x - 5}{3} ② \end{array}$ ．
请结合题意填空，完成本题的解答
①解不等式（2）中的①，得    ▲        ；
②解不等式（2）中的②，得    ▲        ；
③把不等式①和②的解集在数轴上表示出来；

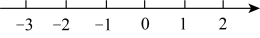
④原不等式组的解集为    ▲         ．

查看试题解析
20. 解下列方程组

(1)、 ${\begin{array}{l} y = - x + 3 \\ x - 2 y + 12 = 0 \end{array}$ ；

(2)、 ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$ ．

查看试题解析
21. 请将下面的推理过程补充完整．

(1)、如图，已知 $A D ∥ B C$ ， $B E$ ， $A C$ 分别 $A D$ ， $B C$ 相交， $∠ B = 70 °$ ， $A D$ 平分 $∠ E A C$ ，求 $∠ C$ 的度数．

解：∵ $A D ∥ B C$ （已知），
∴ $∠ B = ∠ 70 °$ （两直线平行，同位角相等）
∵ $A D$ 平分 $∠ E A C$ （已知），
∴∠= ▲ ∠ ▲ =70°（角平分线的定义）
∵ $A D ∥ B C$ （已知）．
∴ $∠ C = ∠ D A C = 70 °$ （）

(2)、如图， $D E ∥ B C$ ， $A B$ ， $E F$ ， $A C$ 分别与 $D E$ ， $B C$ 相交，且 $∠ 1 = ∠ 2$ ，求证 $E F ∥ A B$ ．

证明：∵ $D E ∥ B C$ （已知），

∴ $∠ 3 = ∠ 4$ （），

∵ $∠ 1 = ∠ 4$ （），

∴ $∠ 1 = ∠ 3$ （）．

又 $∠ 1 = ∠ 2$ （已知），

∴∠ ▲ =∠ ▲ ．

∴ $E F ∥ A B$ （）．

查看试题解析

22. 某兴趣小组随机调查了某市

50

名教师某日行走的步数情况并进行了统计整理，绘制了如下的统计图表（不完整）：

步数/万步	频数	频率
$0 \leq x < 0.4$	$8$	$a$
$0.4 \leq x < 0.8$	$15$	$0.3$
$0.8 \leq x < 1.2$	$12$	$0.24$
$1.2 \leq x < 1.6$	$b$	$0.2$
$1.6 \leq x < 2.0$	$3$	$0.06$
$2.0 \leq x < 2.4$	$2$	$0.04$

请根据以上信息，解答下列问题：

(1)、表格中数据

a =

，

b =

，行走的步数x在

0.8 \leq x < 1.2

范围的教师占调查总体的

%

；

(2)、补全频数分布直方图；

(3)、调查的部分教师中日行走步数超过

1.2

万步（包含

1.2

万步）的人数占（填百分数），由此估计该市约

3600

名教师中，日行走步数超过

1.2

万步（包含

1.2

万步）的教师人数占（填百分数），约有人．

查看试题解析

23. 注意：为了使同学们更好地解答本题，我们提供了一种解思路，你可以依照这个思路接下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．
某茶叶店经销A，B两种茶，第一次购进了A种茶 $30$ 盒，B种茶 $20$ 盒，共花费 $7000$ 元；第二次购进时，两种茶每盒的价格都提高了 $20 %$ ，该店又购进了A种茶 $20$ 盒，B种茶 $15$ 盒，共花费 $6000$ 元，求第一次购进的A，B两种茶每盒的价格．
解题方案：设第一次购进的A种茶每盒的价格为x元，B种茶每盒的价格为y元．

(1)、根据题章，列出方程组 ${\begin{array}{l} ____________ \\ ____________ \end{array}$ ；

(2)、解这个方程组，得 ${\begin{array}{l} x =____________ \\ y =____________ \end{array}$ ．
答：第一次购进的A种茶每盒的价格为元，B种茶每盒的价格为元．

查看试题解析
24. 已知直线 $E F$ 分别与直线 $A B$ ， $C D$ 交于点 $E$ ， $F$ ， $E G$ 平分 $∠ A E F$ 交直线 $C D$ 于点 $G$ ，且 $∠ F E G = ∠ F G E$ ，点 $H$ 是射线 $G D$ 上的一个动点（不与点 $G$ ， $F$ 重合）， $E M$ 平分 $∠ F E H$ ，交直线 $C D$ 于点 $M$ ，过点 $M$ 作 $M N ∥ E G$ ，交 $A B$ 于点 $N$ ，设 $∠ E M N = α$ ， $∠ E H F = β$ ．

(1)、如图①，求证 $A B ∥ C D$ ；

(2)、如图②，当点H在点F的右侧时， $β = 50 °$ ，求 $α$ 的度数．

查看试题解析
25. 如图①，在平面直角坐标系中， $O$ 为原点，已知 $A (a ， 0)$ ， $B (b ， 0)$ ，且 $a$ ， $b$ 满足关系式： $\sqrt{a + 2} + | a + b | = 0$ ，现同时将点 $A$ ， $B$ 向上平移3个单位长度，再向右平移1个单位长度，得到 $A$ ， $B$ 的对应点 $C$ ， $D$ ，连接 $A C$ ， $C D$ ， $D B$ ．

(1)、 $a =$ ， b= ，点C的坐标为，点D的坐标为；

(2)、连接 $C B$ ，在 $x$ 轴上是否存在一点 $P$ ，使得三角形 $B D P$ 的面积等于三角形 $A B C$ 面积的 $\frac{2}{3}$ ？若存在，请求出点P的坐标：若不存在，请说明理由；

(3)、如图②，点 $M$ 是直线 $B D$ 上一个动点连接 $M C$ ， $M O$ ，当点 $M$ 在直线 $B D$ 上运动时，请直接写出 $∠ O M C$ 与 $∠ M C D$ ， $∠ M O B$ 的数量关系．

查看试题解析