四川省成都市郫都区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 下列关于体育运动的图标,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 两人在“石头、剪刀、布”游戏中,两人都出了“剪刀”.这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定性事件3. 下列计算,正确的是( )A、 B、 C、 D、4. 在某一阶段,某商品的售价x(元)与销量y(件)之间存在如下关系:
2. 两人在“石头、剪刀、布”游戏中,两人都出了“剪刀”.这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定性事件3. 下列计算,正确的是( )A、 B、 C、 D、4. 在某一阶段,某商品的售价x(元)与销量y(件)之间存在如下关系:售价x/年
90
100
110
120
130
140
销量y/件
90
80
70
60
50
40
估计当售价x为137元时,销量y可能为( ).
A、33件 B、43件 C、53件 D、63件5. 转动转盘,当转盘停止转动时,指针落在红色区域的可能性最大的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在中,的度数是( )
6. 如图,在中,的度数是( ) A、 B、 C、 D、7. 如图,在中,边上的高为( )
A、 B、 C、 D、7. 如图,在中,边上的高为( ) A、线段 B、线段 C、线段 D、线段8. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( )
A、线段 B、线段 C、线段 D、线段8. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( )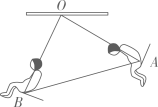 A、70° B、60° C、50° D、40°
A、70° B、60° C、50° D、40°二、填空题
-
9. 夷人多封锁,国人当自强.国内某大学开设了芯片研究学院,研发出了厚度约为米的芯片.用科学记数法表示数据应为 .10. 若 , , 则 .11. 如图,直线 , 若 , 则的大小为 .
 12. 某图书出租店图书的租金y(元)与出租的天数x(天)之间的函数图象如图所示,结合图象计算可知:两天后每过一天租金增加元.
12. 某图书出租店图书的租金y(元)与出租的天数x(天)之间的函数图象如图所示,结合图象计算可知:两天后每过一天租金增加元. 13. 如图,在中, , 平分交于点 , , , 则 .
13. 如图,在中, , 平分交于点 , , , 则 .
三、解答题
-
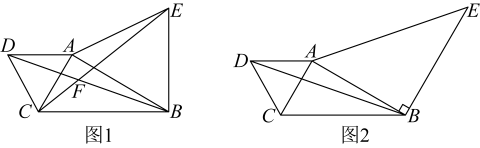
14. 按要求解答下列各题(1)、计算: .(2)、先化简,再求值: , 其中 , .15. 如图,在中,是的垂直平分线,于点D,且D为的中点.
 (1)、求证:;(2)、若 , 求的度数.16. 为鼓励学生多读书,读好书,七年级(8)班班主任精选了《朝花夕拾》、《平凡的世界》、《长征》、《红岩》、《文化苦旅》共5种书,准备送给学生.(1)、若上述5种书各有2本,小明从中任选一本,选中《红岩》的概率是多少?(2)、若上述5种书各有3本,小明从上述5种书中任选一本,选中《长征》的概率是 , 班主任老师只需要增加几本《长征》书?17. 如图, , 和的角平分线交于点 , 交于点 . (解答过程要求写出每步推导的理由)
(1)、求证:;(2)、若 , 求的度数.16. 为鼓励学生多读书,读好书,七年级(8)班班主任精选了《朝花夕拾》、《平凡的世界》、《长征》、《红岩》、《文化苦旅》共5种书,准备送给学生.(1)、若上述5种书各有2本,小明从中任选一本,选中《红岩》的概率是多少?(2)、若上述5种书各有3本,小明从上述5种书中任选一本,选中《长征》的概率是 , 班主任老师只需要增加几本《长征》书?17. 如图, , 和的角平分线交于点 , 交于点 . (解答过程要求写出每步推导的理由) (1)、求的度数;(2)、若 , 求证: .18. 如图,在中, , . 过点作 , 且取 , 连接交于点 .
(1)、求的度数;(2)、若 , 求证: .18. 如图,在中, , . 过点作 , 且取 , 连接交于点 . (1)、求证:;(2)、作于点 , 连接 .
(1)、求证:;(2)、作于点 , 连接 .①求证:;
②设 , 求与的数量关系.
四、填空题
-
19. 若 , 则的值为 .20. 如图,把一个长方形纸条沿折叠,若 , 则度.
 21. 若、、是三角形的三边,化简: .22. 如图,在5×5的正方形网格中,点A、在格点上,在该网格中取一个格点 , 能使A、、为顶点的等腰三角形中为等腰直角三角形的概率为 .
21. 若、、是三角形的三边,化简: .22. 如图,在5×5的正方形网格中,点A、在格点上,在该网格中取一个格点 , 能使A、、为顶点的等腰三角形中为等腰直角三角形的概率为 . 23. 如图,在四边形中, , , 点、分别在、上,当的周长最小时,用的代数式表示 , 则 .
23. 如图,在四边形中, , , 点、分别在、上,当的周长最小时,用的代数式表示 , 则 .
五、解答题
-
24. 某公交车每月的支出费用为4000元,票价为2元/人次,设每月有人次乘坐该公交车,每月收入与支出的差额为元.(1)、写出下列表格中对应的值;
(人)
1000
1500
2000
2500
3000
3500
…
(元)
…
(2)、根据(1)中表格的数据,直接写出与之间的关系式;直接回答,当达到多少时,该公交车才不会亏损?(3)、若该公交车每月的收入与支出的差额要达到8000元,求的值.