湖南省长沙市雨花区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $m > n$ ，则下列各式中正确的是（）

A、 $m + 2 < n + 2$ B、 $m - 3 < n - 3$ C、 $- 5 m < - 5 n$ D、 $\frac{m}{6} < \frac{n}{6}$

查看试题解析
2. 下列调查中，适合用全面调查的是（）

A、某厂生产的电灯使用寿命 B、全国初中生视力情况 C、七年级某班学生身高情况 D、某种饮料产品合格率

查看试题解析
3. 估计 $\sqrt{23}$ 的值在（）

A、 $3$ 和 $4$ 之间 B、 $4$ 和 $5$ 之间 C、 $5$ 和6之间 D、6和 $7$ 之间

查看试题解析
4. 下列说法正确的是（）

A、±5是25的算术平方根 B、±4是64的立方根 C、-2是-8的立方根 D、(-4)²的平方根是-4

查看试题解析
5. 周末回家，妈妈买了苹果、梨、柚子、橘子四种水果共50个，如果把苹果的个数加4，梨的个数减4，柚子的个数乘4，橘子的个数除以4，最后四种水果的个数相等，那么橘子的个数是（）

A、8个 B、12个 C、16个 D、32个

查看试题解析
6. 数a，b，c，d在数轴上对应点的位置如图所示，则下列结论正确的是（　　）

A、d表示的数可能是- $\sqrt{3}$ B、c－b>0 C、 $\sqrt{(c - a)^{2}}$ =a－c D、|b|－|a|＝a－b

查看试题解析
7. 如图是某公园里一处矩形风景欣赏区ABCD ，长AB＝100米，宽BC＝50米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为2米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（　　）

A、148米 B、196米 C、198米 D、200米

查看试题解析
8. 若满足方程组 ${\begin{cases} 3 x + y = m + 3 \\ 2 x - y = 2 m - 1 \end{cases}$ 的 $x$ 与 $y$ 互为相反数，则 $m$ 的值为（）

A、11 B、-1 C、1 D、-11

查看试题解析
9. 下面是 $A ， B$ 两球从不同高度自由下落到地面后反弹高度的折线统计图，根据图中信息，在实验数据范围内，以下说法错误的是（）

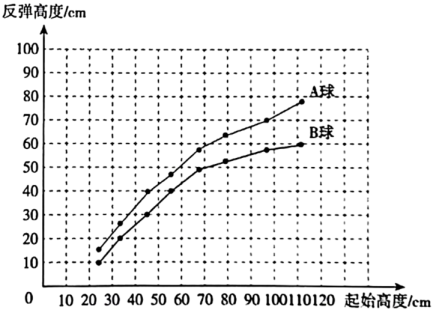A、 $A$ 球与 $B$ 球相比， $A$ 球的弹性更大 B、随着起始高度增加，两球的反弹高度也会增加 C、两球的反弹高度均不会超过相应的起始高度 D、将 $A$ 球从68cm的高度自由下落，第二次接触地面后的反弹高度小于40cm

查看试题解析
10. 如图，动点 $A_{0}$ 在平面直角坐标系中从坐标原点出发，第一次运动到 $A_{1} (1 ， 1)$ ，第二次运动到 $A_{2} (2 ， 1)$ ，第三次运动到 $A_{3} (3 ， 0)$ ，第四次运动到 $A_{4} (4 ， - 1)$ ，第五次运动到 $A_{5} (5 ， - 1)$ ，第六次运动到 $A_{6} (6 ， 0)$ ，第七次运动到 $A_{7} (7 ， 1)$ ， …，按这样的运动规律，经过第2023次运动后，点 $A_{2023}$ 的坐标是（）

A、 $(2023 ， 1)$ B、 $(337 ， 1)$ C、 $(2023 ， - 1)$ D、 $(2023 ， 0)$

查看试题解析

二、填空题

11. 若 ${\begin{array}{l} x = 1 ， \\ y = 2 \end{array}$ 是方程 $2 x + a y = 8$ 的解，则a的值为．

查看试题解析
12. 已知点 $A (a + 2 ， 5)$ 、 $B (- 4 ， 1 - 2 a)$ ，若直线 $A B$ 平行于x轴，则 $a =$ ．

查看试题解析
13. 已知 ${\begin{array}{l} 2 x + 3 y = 13 \\ 3 x + 2 y = 17 \end{array}$ ，则 $x + y$ 的值是．

查看试题解析
14. 如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为．

查看试题解析
15. 如图1，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长为20，宽为10的长方形，如图2，则图2中（1）部分的面积是．

查看试题解析
16. 如图，下列条件：①∠1＝∠2；②∠BAD+∠ADC＝180°；③∠ABC＝∠ADC；④∠3＝∠4；其中能判定AB∥CD的是（填序号）．

查看试题解析

三、解答题

17. 计算： ${(- 2)}^{3} \times \sqrt{{(- 4)}^{2}} + \sqrt[3]{{(- 4)}^{3}} \times {(\frac{1}{2})}^{2} - \sqrt{9}$

查看试题解析
18. 解方程组： ${\begin{array}{l} x - y = 1 \\ x + 3 y = 9 \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} 5 x < 1 + 4 x \\ \frac{1 - x}{2} \leq \frac{x + 4}{3} \end{array}$ ，并在数轴上表示不等式组的解集．

查看试题解析

20. 清朝康熙年间编校的《全唐诗》包含四万多首诗歌，逾三百万字，是后人研究唐诗的重要资源．小云利用统计知识分析《全唐诗》中李白和杜甫作品的风格差异．下面给出了部分信息：

a ．《全唐诗》中，李白和杜甫分别有896和1158首作品．

b ．二人作品中与“风”相关的词语频数统计表如下：

词语

频数

诗人

春风

东风

清风

悲风

秋风

北风

李白

杜甫

c ．通过统计二人的个性化用字，可绘制一种视觉效果更强的“词云图”，出现次数较多的关键字被予以视觉上的突出．

注：在文学作品中，东风即春风，常含有生机勃勃之意和喜春之情，如：等闲识得东风面，万紫千红总是春；北风通常寄寓诗人凄苦的情怀，抒写伤别之情，如：千里黄云白日曛，北风吹雁雪纷纷．

根据以上信息，回答下列问题：

(1)、补全条形统计图：

(2)、在与“风”相关的词语中，李白最常使用的词语是，大约每首诗歌中就会出现一次该词语（结果取整数），而杜甫最常使用的词语是；

(3)、下列推断合理的是．

①相较于杜甫，与“风”有关的词语在李白的诗歌中更常见；

②个性化用字中，李白最常使用的汉字是“水”，杜甫则是“江”；

③李白更常用“风”表达喜悦，而杜甫更常用“风”表达悲伤．

查看试题解析

21. 为了参加西部博览会，资阳市计划印制一批宣传册．该宣传册每本共10页，由A、B两种彩页构成．已知A种彩页制版费300元/张，B种彩页制版费200元/张，共计2400元．（注：彩页制版费与印数无关）

(1)、每本宣传册A、B两种彩页各有多少张？

(2)、据了解，A种彩页印刷费2.5元/张，B种彩页印刷费1.5元/张，这批宣传册的制版费与印刷费的和不超过30900元．如果按到资阳展台处的参观者人手一册发放宣传册，预计最多能发给多少位参观者？

查看试题解析
22. 方法迁移与运用：

(1)、已知方程组 ${\begin{array}{l} 3 a - 2 b = 11 \\ 4 a + 3 b = 9 \end{array}$ 的解为 ${\begin{array}{l} a = 3 \\ b = - 1 \end{array}$ ，则由 ${\begin{array}{l} 3 (x + y) - 2 (x - y) = 11 \\ 4 (x + y) + 3 (x - y) = 9 \end{array}$ 可得出 $x + y =$ ， $x - y =$ ，从而求得 $x =$ ， $y =$ ；

(2)、解方程组 ${\begin{array}{l} 3 (x + y) + 2 (x - y) = 36 \\ 2 (x + y) - 3 (x - y) = 24 \end{array}$ ．

查看试题解析
23. 如图，E ， G分别是AB ， AC上的点，F ， D是BC上的点，连接EF ， AD ， DG ，如果 $A B ∥ D G$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、判断AD与EF的位置关系，并说明理由；

(2)、若DG是 $∠ A D C$ 的平分线， $∠ 2 = 140 °$ ，求 $∠ B$ 的度数．

查看试题解析
24. 【提出问题】已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围．
【分析问题】先根据已知条件用一个量如取y表示另一个量如x，然后根据题中已知量x的取值范围，构建另一个量y的不等式，从而确定该量y的取值范围，同法再确定另一未知量x的取值范围，最后利用不等式性质即可获解．

【解决问题】解：∵x﹣y=2，∴x=y+2．

又∵x＞1，∴y+2＞1，∴y＞﹣1．

又∵y＜0，∴﹣1＜y＜0，…①

同理得1＜x＜2…②

由①+②得﹣1+1＜y+x＜0+2．

∴x+y的取值范围是0＜x+y＜2．

【尝试应用】已知x﹣y=﹣3，且x＜﹣1，y＞1，求x+y的取值范围．

查看试题解析
25. 对于平面直角坐标系xOy中的任意一点 $P (x ， y)$ ，给出如下定义：记 $a = x + y$ ， $b = - y$ ，将点 $M (a ， b)$ 与 $N (b ， a)$ 称为点P的一对“相伴点”．例如：点 $P (2 ， 3)$ 的一对“相伴点”是点 $(5 ， - 3)$ 与 $(- 3 ， 5)$ ．

(1)、点 $Q (4 ， - 1)$ 的一对“相伴点”的坐标是与；

(2)、若点 $A (8 ， y)$ 的一对“相伴点”重合，则y的值为；

(3)、若点B的一个“相伴点”的坐标为 $(- 1 ， 7)$ ，求点B的坐标；

查看试题解析