湖南省长沙市雅礼教育集团2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数为无理数的是（）

A、 $0.618$ B、 $\frac{22}{7}$ C、 $\sqrt{5}$ D、 $\sqrt[3]{- 27}$

查看试题解析
2. 下列点的坐标在第四象限的是（）

A、 $(5 ， 2)$ B、 $(- 6 ， 3)$ C、 $(- 4 ， - 6)$ D、 $(3 ， - 4)$

查看试题解析
3. 若 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ 是关于x．y的方程2x﹣y+2a=0的一个解，则常数a为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 若 $m ＞ n ＞ 0$ ，下列不等式不成立的是（）

A、 $m - 2 > n - 2$ B、 $2 m + 1 > 2 n + 1$ C、 $- \frac{m}{2} ＞ - \frac{n}{2}$ D、 $\sqrt{m} ＞ \sqrt{n}$

查看试题解析
5. 下列调查方式合适的是（）

A、为了解全国中学生的视力状况，采用普查的方式 B、为了解某款新型笔记本电脑的使用寿命，采用普查的方式 C、调查全省七年级学生对新型冠状病毒传播途径的知晓率，采用抽样调查的方式 D、对“天问一号”火星探测器零部件的检查，采用抽样调查的方式

查看试题解析
6. 如图，一扇窗户打开后，用窗钩 $A B$ 可将其固定，这里所运用的几何原理是（）

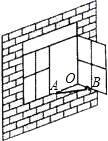A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短

查看试题解析
7. 如图，点E、点F在 $B C$ 上， $B E = C F$ ， $∠ B = ∠ C$ ，添加一个条件，不能证明 $△ A B F ≌ △ D C E$ 的是（）

A、 $∠ A = ∠ D$ B、 $∠ A F B = ∠ D E C$ C、 $A B = D C$ D、 $A F = D E$

查看试题解析
8. 《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸：屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长水，长木还剩余1尺，问木长多少尺。设木长为x尺，绳子长为y尺，则下列符合题意的方程组是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ C、 ${\begin{array}{l} y = 4.5 - x \\ \frac{1}{2} y = x + 1 \end{array}$ D、 ${\begin{array}{l} y = x - 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ，且外角 $∠ A B D = 130 °$ ，则外角 $∠ A C E$ 的度数是（）

A、 $110 °$ B、 $120 °$ C、 $130 °$ D、 $140 °$

查看试题解析
10. 以关于x、y的方程组 ${\begin{array}{l} 2 x + y = m + 7 \\ x + 2 y = 8 - m \end{array}$ 的解为横纵坐标的点 $P (x ， y)$ 在第一象限，那么m的取值范围在数轴上应表示为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 在 $0$ ， $(- \frac{1}{3})^{2}$ ， $- π$ ， $- 2$ 四个数中，最小的实数是．

查看试题解析
12. 点 $P (- 2 ， 2)$ 先向左平移3个单位，再向下平移3个单位得到点Q ，则点Q的坐标为．

查看试题解析
13. 若一个正多边形的内角和是外角和的 $2$ 倍，则这个正多边形的边数为．

查看试题解析
14. 如图，已知 $a ∥ b$ ， $∠ 1 = 55 °$ ， $∠ A = 25 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
15. 若三角形的两边长是a和b ，且满足 ${\begin{array}{l} 2 a + b = 10 \\ a + 2 b = 11 \end{array}$ ，则这个三角形的第三边c的取值范围是．

查看试题解析
16. 如图，已知P(3，3)，点B、A分别在x轴正半轴和y轴正半轴上，∠APB＝90°，则OA＋OB＝.

查看试题解析

三、解答题

17. 计算： $(- 1)^{2023} + \sqrt[3]{- 8} + \sqrt{25} + | \sqrt{3} - 2 |$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{2 x + 2}{5} > \frac{x + 1}{2} \end{array}$ ，并在数轴上表示此不等式组的解集．

查看试题解析
19. 工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知 $∠ A O B$ 是一个任意角，在边 $O A$ ， $O B$ 上分别取 $O M = O N$ ，移动角尺，使角尺两边相同的刻度分别与点M ， N重合，则过角尺顶点C的射线 $O C$ 便是 $∠ A O B$ 的角平分线．请完成下列问题：

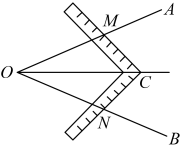(1)、这种做法的依据是（填序号）．
① $A S A$ ② $S A S$ ③ $A A S$ ④ $S S S$

(2)、请证明 $O C$ 平分 $∠ A O B$ ．

查看试题解析
20. 智能手机等高科技产品正越来越严重地伤害青少年的眼睛，保护视力，刻不容缓．长沙市某校为了解学生的视力状况，培养学生保护视力的意识，对该校部分学生做了一次主题为“保护视力爱眼护眼”的调查活动，根据近视程度的不同将学生分为A、B、C、D、E五类，其中A表示视力良好、B表示轻度近视（ $300$ 度以下）、C表示中度近视（ $300$ 度～ $600$ 度）、D表示高度近视（ $600$ 度～ $900$ 度）、E表示超高度近视（ $900$ 度以上）．学校根据调查情况进行了统计，并绘制了如下两幅不完整的统计图：
请你结合图中信息，解答下列问题：

(1)、参与本次调查活动的学生有人，

(2)、补全条形统计图；

(3)、求“视力良好”对应扇形的圆心角度数；

(4)、该校共有 $2900$ 名学生，请你估计该校“高度近视”和“超高度近视”的学生总人数．

查看试题解析
21. 如图， $△ A B C$ 中， $A D$ 是 $△ A B C$ 的中线， $A E$ 是 $△ A B C$ 的角平分线， $A H$ 是 $△ A B C$ 的高．

(1)、若 $△ A B D$ 的面积为8， $A H = 4$ ，求 $B C$ 的长；

(2)、若 $∠ B = 30 ° ， ∠ E A H = 20 °$ ，求 $∠ C$ 的度数．

查看试题解析
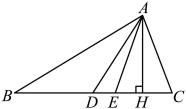22. 在一次高速铁路建设中，某渣土运输公司承包了某标段的土方运输任务，拟派出大、小两种型号的渣土运输车运输土方．已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨，5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨．

(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨？

(2)、该渣土运输公司决定派出大、小两种型号渣土运输车共20辆参与运输土方，若每次运输土方总量不小于148吨，且小型渣土运输车至少派出2辆，则有哪几种派车方案？

查看试题解析
23. 如图， $∠ B A D = ∠ C A E = 90 °$ ， $A B = A D$ ， $A E = A C$ ， $C E$ 经过点D ．

(1)、求证： $△ A B C ≌ △ A D E$ ；

(2)、 $B C$ 和 $D E$ 有何数量和位置关系？请说明理由；

(3)、若 $A C = 6$ ，求四边形 $A B C D$ 的面积．

查看试题解析
24. 我们约定：若一元一次方程的解在一元一次不等式组的解集范围内，则称该一元一次方程为该不等式组的“美美与共方程”，例如：方程 $x - 2 = 2$ 的解为 $x = 4$ ，而不等式组 ${\begin{array}{l} x - 1 > 2 \\ x - 2 < 3 \end{array}$ 的解集为 $3 < x < 5$ ，不难发现 $x = 4$ 在 $3 < x < 5$ 的范围内，所以方程 $x - 2 = 2$ 是不等式组 ${\begin{array}{l} x - 1 > 2 \\ x - 2 < 3 \end{array}$ 的“美美与共方程”．

(1)、在一元一次方程① $6 x - 7 ＝ 4 x - 5$ ；② $2 x + 5 = 3 (x - 1)$ ；③ $\frac{x - 3}{- 5} = \frac{3 x + 4}{15}$ 中，不等式组 ${\begin{array}{l} 5 x + 2 ＞ 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ 的“美美与共方程”是；（填序号）

(2)、若关于x的方程 $\frac{x - 1}{2} - k = 0$ 是不等式组 ${\begin{array}{l} 5 x - 3 (x - 2) > 1 \\ \frac{x + 1}{6} \geq \frac{2 x - 5}{4} + 1 \end{array}$ 的“美美与共方程”，求k的取值范围；

(3)、若关于x的方程 $\frac{x - 5}{6} = \frac{m}{3} - 1$ 是关于x的不等式组 ${\begin{array}{l} 2 (x + 1) > m - 1 \\ \frac{x - 1}{2} \geq \frac{2 x + 1}{3} - 2 \end{array}$ 的“美美与共方程”，且此时该不等式组有7个整数解，若 $M = 2 m + 3 n - p ， 3 m - n + p = 4 ， m + n + p = 6$ ，求M的取值范围．

查看试题解析
25. 如图，四边形 $A B C D$ 在平面直角坐标系中， $A (0 ， 3) ， B (- 2 ， 0) ， D (3 ， 0) ， A B ⊥ B C ，$ $A B = B C$ ，在x轴正半轴上有一点P ，过点P作 $P Q ⊥ A P$ ，交 $C D$ 延长线于点Q ．

(1)、求点C的坐标；

(2)、当 $C P ⊥ O D$ 时，求证： $P A = P Q$ ；

(3)、当点P在点D右侧时，连接 $B Q$ ，在 $D A$ 的延长线上存在一点F ，使得 $∠ Q B F = 45 °$ ，求 $Q F 、 Q C 、 A F$ 之间的数量关系，并说明理由．

查看试题解析