山东省济南市高新区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
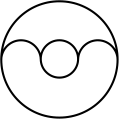 B、
B、 C、
C、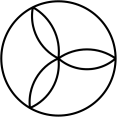 D、
D、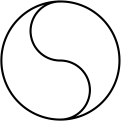 2. 下列各等式从左边到右边的变形中,是因式分解的是( )A、 B、 C、 D、3. 有一个数不小于a,这个数在数轴上表示,正确的是( )A、
2. 下列各等式从左边到右边的变形中,是因式分解的是( )A、 B、 C、 D、3. 有一个数不小于a,这个数在数轴上表示,正确的是( )A、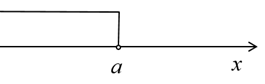 B、
B、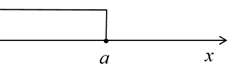 C、
C、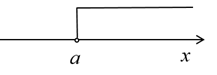 D、
D、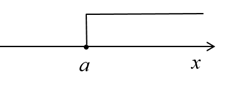 4. 如图,在一次实践活动课上,小明为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 , 然后取线段 , 的中点 , , 测量出 , 于是可以计算出池塘 , 两点间的距离是( )
4. 如图,在一次实践活动课上,小明为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 , 然后取线段 , 的中点 , , 测量出 , 于是可以计算出池塘 , 两点间的距离是( )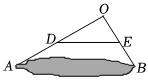 A、 B、 C、 D、5. 在中, , , 则的度数是( )A、 B、 C、 D、6. 计算:( )A、a B、 C、 D、7. 菱形的对角线长分别为6和8,它的面积为( )A、5 B、20 C、24 D、488. 已知方程有两个实数根,则的取值范围是( )A、 B、 C、且 D、且9. 若干辆载重为的卡车来运载货物,若每辆卡车只装 , 则剩下货物;若每辆卡车装5t,则最后一辆汽车不满也不空,问:可能有( )辆汽车.A、6 B、7 C、8 D、910. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )
A、 B、 C、 D、5. 在中, , , 则的度数是( )A、 B、 C、 D、6. 计算:( )A、a B、 C、 D、7. 菱形的对角线长分别为6和8,它的面积为( )A、5 B、20 C、24 D、488. 已知方程有两个实数根,则的取值范围是( )A、 B、 C、且 D、且9. 若干辆载重为的卡车来运载货物,若每辆卡车只装 , 则剩下货物;若每辆卡车装5t,则最后一辆汽车不满也不空,问:可能有( )辆汽车.A、6 B、7 C、8 D、910. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )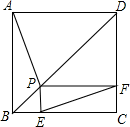 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
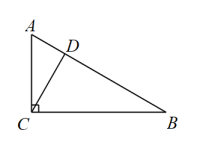
11. 分解因式: .12. 点A(3,2)向右平移2个单位长度得到A′,则A′的坐标为.13. 如图,在中,于D , 若 , 则 .
 14. 已知方程 , 则 .15. 小刚开学后,第一次测试数学得了70分,语文得了84分,则英语至少得 分,才能使三科平均分不低于80分.16. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .
14. 已知方程 , 则 .15. 小刚开学后,第一次测试数学得了70分,语文得了84分,则英语至少得 分,才能使三科平均分不低于80分.16. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .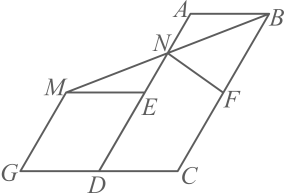
三、解答题
-
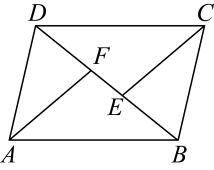
17. 解方程:18. 解不等式组 , 并写出它的所有正整数解.19. 如图,平行四边形中,点E , F在对角线上,且 . 求证: .
 20. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上.
20. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上. (1)、画出将向左平移个单位长度得到的;(2)、画出绕点顺时针旋转后得到的 , 并写出的坐标.21. 如图,BE是△ABC的角平分线,点D在AB上,且 .
(1)、画出将向左平移个单位长度得到的;(2)、画出绕点顺时针旋转后得到的 , 并写出的坐标.21. 如图,BE是△ABC的角平分线,点D在AB上,且 .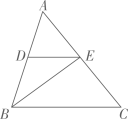 (1)、求证:;(2)、若 , , 求的大小.22. 如图,在中, , D是的中点,过点A作 , 且 , 连接 .
(1)、求证:;(2)、若 , , 求的大小.22. 如图,在中, , D是的中点,过点A作 , 且 , 连接 .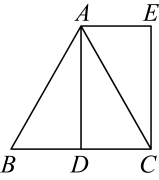 (1)、求证:四边形是矩形:(2)、若 , , 求的长.23. 随着“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注,体育用品需求增加,某商店决定购进A、B两种羽毛球拍进行销售,已知每副A种球拍的进价比每副B种球拍贵20元,用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同.(1)、求A、B两种羽毛球拍每副的进价;(2)、若该商店决定购进这两种羽毛球拍共100副,考虑市场需求和资金周转,用于购买这100副羽毛球拍的资金不超过5900元,那么该商店最多可购进A种羽毛球拍多少副?24. 定义:对任意一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与的商记为 .
(1)、求证:四边形是矩形:(2)、若 , , 求的长.23. 随着“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注,体育用品需求增加,某商店决定购进A、B两种羽毛球拍进行销售,已知每副A种球拍的进价比每副B种球拍贵20元,用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同.(1)、求A、B两种羽毛球拍每副的进价;(2)、若该商店决定购进这两种羽毛球拍共100副,考虑市场需求和资金周转,用于购买这100副羽毛球拍的资金不超过5900元,那么该商店最多可购进A种羽毛球拍多少副?24. 定义:对任意一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与的商记为 .例如: , 对调个位数字与十位数字得到新两位数 , 新两位数与原两位数的和为 , 和与的商为 , 所以 .
根据以上定义,回答下列问题:
(1)、填空:下列两位数: , , 中,“慧泉数”为;(2)、计算:①;②;
(3)、如果一个“慧泉数”的十位数字是 , 个位数字是 , 另一个“慧泉数”的十位数字是 , 个位数字是 , 且满足 , 求 .25. 如图1,在平面直角坐标系中,直线分别与x轴、y轴相交于点A、B , 是的角平分线,交直线于点C .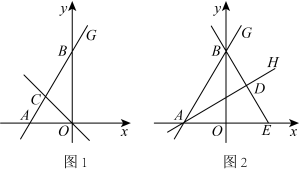 (1)、求点C的坐标;(2)、如图2,是的角平分线,过点B作的垂线交于点D , 交x轴于点E求直线的解析式;(3)、在x轴上寻找点F使得为等腰三角形,请直接写出点F的坐标.26.
(1)、求点C的坐标;(2)、如图2,是的角平分线,过点B作的垂线交于点D , 交x轴于点E求直线的解析式;(3)、在x轴上寻找点F使得为等腰三角形,请直接写出点F的坐标.26.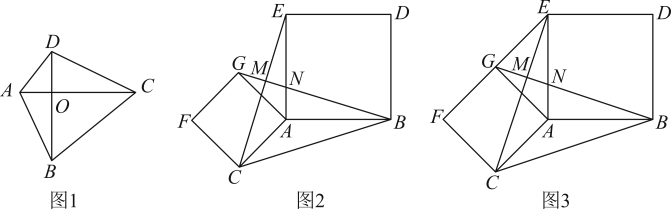 (1)、【探究发现】如图1,在四边形中,对角线 , 垂足是O , 则图中出现4个直角三角形,在中, , 则有 , 据此探索与的值是否相等,并说明理由.(2)、【拓展迁移】如图2,以三角形的边为边向外作正方形和正方形 , 求证: .(3)、如图3,在(2)小题条件不变的情况下,连接GE , 若 , 求的长.
(1)、【探究发现】如图1,在四边形中,对角线 , 垂足是O , 则图中出现4个直角三角形,在中, , 则有 , 据此探索与的值是否相等,并说明理由.(2)、【拓展迁移】如图2,以三角形的边为边向外作正方形和正方形 , 求证: .(3)、如图3,在(2)小题条件不变的情况下,连接GE , 若 , 求的长.