山东省济南市钢城区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 在一个不透明的袋子里,装有3个红球,2个白球,1个黄球,它们除颜色外都相同,从袋中任意摸出一个球为白球的概率是( )A、 B、 C、 D、2.
如图,直线a∥b,AC丄AB,AC交直线b于点C,∠1=65°,则∠2的度数是( )
 A、65° B、50° C、35° D、25°3. 有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③无理数包括正无理数、0、负无理数;④同一平面内,垂直于同一条直线的两条直线平行.是真命题的命题的个数有( )个.A、1 B、2 C、3 D、44. 若m> -1,则下列各式中错误的是( )A、6m> -6 B、-5m< -5 C、m+1>0 D、1-m<25. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )
A、65° B、50° C、35° D、25°3. 有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③无理数包括正无理数、0、负无理数;④同一平面内,垂直于同一条直线的两条直线平行.是真命题的命题的个数有( )个.A、1 B、2 C、3 D、44. 若m> -1,则下列各式中错误的是( )A、6m> -6 B、-5m< -5 C、m+1>0 D、1-m<25. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( ) A、 B、 C、 D、6. 不等式组的解集为 , 在下列数轴上表示正确的是( )A、
A、 B、 C、 D、6. 不等式组的解集为 , 在下列数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 如果等腰三角形有两条边长分别为5,6,那么该等腰三角形的周长等于( )A、16 B、17 C、16或17 D、17或188. 已知 是二元一次方程组 的解,则 的值为( )A、-1 B、1 C、2 D、39. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( )
7. 如果等腰三角形有两条边长分别为5,6,那么该等腰三角形的周长等于( )A、16 B、17 C、16或17 D、17或188. 已知 是二元一次方程组 的解,则 的值为( )A、-1 B、1 C、2 D、39. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( ) A、25 B、22 C、20 D、1410. 若该不等式组无解,则的取值范围是( )A、 B、 C、 D、
A、25 B、22 C、20 D、1410. 若该不等式组无解,则的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为 .
 12. 如图所示的是小明家的地板砖的一部分(图中所有三角形都是等腰直角三角形).随机抛一个小球停留在某块地板砖上,则小球停留在阴影区域的概率是 .
12. 如图所示的是小明家的地板砖的一部分(图中所有三角形都是等腰直角三角形).随机抛一个小球停留在某块地板砖上,则小球停留在阴影区域的概率是 . 13. 若关于 , 的二元一次方程组的解互为相反数,则 .14. 《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知6个大桶加上1个小桶可以盛酒4斛(斛,音hú , 是古代一种容量单位),1个大桶加上6个小桶可以盛酒3斛.1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶可以盛酒斛、1个小桶可以盛酒斛.根据题意,可列方程组为 .15. 如图,直线 与直线 在同一平面直角坐标系中的图像如图所示,则关于x的不等式 的解集为 .
13. 若关于 , 的二元一次方程组的解互为相反数,则 .14. 《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知6个大桶加上1个小桶可以盛酒4斛(斛,音hú , 是古代一种容量单位),1个大桶加上6个小桶可以盛酒3斛.1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶可以盛酒斛、1个小桶可以盛酒斛.根据题意,可列方程组为 .15. 如图,直线 与直线 在同一平面直角坐标系中的图像如图所示,则关于x的不等式 的解集为 .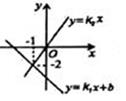 16. 定义新运算:对于任意实数、约定关于的一种运算如下: . 例如: . 若 , 且 , 则的值是 .
16. 定义新运算:对于任意实数、约定关于的一种运算如下: . 例如: . 若 , 且 , 则的值是 .三、解答题
-
17. 解方程组:18. 解不等式组把它的解集在数轴上表示出来19. 如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置。(保留作图痕迹)。
 20. 我市为了打造湿地公园,今年计划改造一片绿化地种植 , 两种景观树.种植棵种、棵种景观树需要元,种植棵种、棵种景观树需要元.种植每棵种景观树和每棵种景观树各需要多少元?21. 如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,两个滑梯的倾斜角和的度数和为 , 并证明你的结论.
20. 我市为了打造湿地公园,今年计划改造一片绿化地种植 , 两种景观树.种植棵种、棵种景观树需要元,种植棵种、棵种景观树需要元.种植每棵种景观树和每棵种景观树各需要多少元?21. 如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,两个滑梯的倾斜角和的度数和为 , 并证明你的结论. 22. 今年“6.18”互联网促销期间,某网红店开展有奖促销活动,凡进店购物的顾客均有转动8等分圆盘的机会,(如图),如果规定当圆盘停下来时指针指向1就中一等奖,指向3或8就中二等奖,指向2或4或6就中三等奖;指向其余数字不中奖.
22. 今年“6.18”互联网促销期间,某网红店开展有奖促销活动,凡进店购物的顾客均有转动8等分圆盘的机会,(如图),如果规定当圆盘停下来时指针指向1就中一等奖,指向3或8就中二等奖,指向2或4或6就中三等奖;指向其余数字不中奖. (1)、转动转盘,中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、6月18日这天有1600人参与这项活动,估计这天获得一等奖的人数是多少?23. 如图,AB//CD , ∠BCD=70°,∠CBF=20°,∠BFE=130°.
(1)、转动转盘,中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、6月18日这天有1600人参与这项活动,估计这天获得一等奖的人数是多少?23. 如图,AB//CD , ∠BCD=70°,∠CBF=20°,∠BFE=130°. (1)、求证AB∥EF;(2)、若∠CEF=70°,求∠ACB的度数.24. 为建设高质量教育体系,构建教育良好生态,促进学生德、智、体、美、劳全面发展.某校利用课余活动时间强健同学们的体魄,增设了羽毛球社团,深受同学们的喜爱,由于报名人数较多,现需要购买一批羽毛球拍和羽毛球.已知某知名品牌的羽毛球拍一副元,羽毛球一个元,甲、乙两个商店给出如下优惠方案:
(1)、求证AB∥EF;(2)、若∠CEF=70°,求∠ACB的度数.24. 为建设高质量教育体系,构建教育良好生态,促进学生德、智、体、美、劳全面发展.某校利用课余活动时间强健同学们的体魄,增设了羽毛球社团,深受同学们的喜爱,由于报名人数较多,现需要购买一批羽毛球拍和羽毛球.已知某知名品牌的羽毛球拍一副元,羽毛球一个元,甲、乙两个商店给出如下优惠方案:甲:每副羽毛球拍打九五折,每个羽毛球打九折;
乙:买一副羽毛球拍送两个羽毛球.
现需要购买羽毛球拍副和羽毛球个).
(1)、在甲、乙两个商店购买的总费用分别为元,元,求 , 与的函数关系式;(2)、请你帮学校设计方案,说明在哪家商店购买更加划算.25. 【活动回顾】:八年级下册教材中,我们曾探究过“函数的图象上点的坐标的特征”,了解了一元一次不等式的解集与相应的一次函数图象上点的坐标的关系.
发现:一元一次不等式的解集是函数图象在轴上方的点的横坐标的集合.
结论:一元一次不等式:(或)的解集,是函数图象在轴上方(或轴下方)部分的点的横坐标的集合.
【解决问题】:
(1)、如图1,一次函数的图象经过点 , 则不等式的解集是 .(2)、如图2,两条直线的交点坐标为 , 方程的解是;不等式的解是 .(3)、【拓展延伸】如图3,一次函数和的图象相交于点 , 分别与轴相交于点和点 .①求点 , 的坐标;
②结合图象,直接写出关于的不等式组的解集是 .
26. 在中, , 点是直线上一点不与、重合 , 以为一边在的右侧作 , 使 , , 连接E .(1)、如图1,当点在线段上,如果 .
①则与全等吗?请说明理由;
②求的度数;
(2)、如图2,如果 , 当点在线段上移动,则的度数是; (3)、如图2,当点在线段上,如果 , 点为中边上的一个动点与、均不重合 , 当点运动到什么位置时,的周长最小?
(3)、如图2,当点在线段上,如果 , 点为中边上的一个动点与、均不重合 , 当点运动到什么位置时,的周长最小?