山东省济南市济阳区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 下列运算正确的是( ).A、 B、 C、 D、2. 以下是清华大学、北京大学、上海交通大学、中国人民大学四个大学的校徽,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在一个不透明的袋中有6个只有颜色不同的球,其中4个黑球和2个白球.从袋中任意摸出一个球,是黑球的概率为( )A、 B、 C、 D、4. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )
3. 在一个不透明的袋中有6个只有颜色不同的球,其中4个黑球和2个白球.从袋中任意摸出一个球,是黑球的概率为( )A、 B、 C、 D、4. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )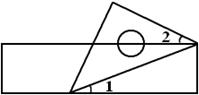 A、15° B、20° C、25° D、40°5. 有一个长为10,宽为6的长方形,若将长方形的宽增加 , 长不变,则增加的长方形的面积y与x之间的关系式为( )A、 B、 C、 D、6. 某商场为了吸引顾客,设计了如图所示的可自由转动的转盘,当指针指向阴影部分时,顾客可获得一份奖品,那么顾客获奖的概率为( )
A、15° B、20° C、25° D、40°5. 有一个长为10,宽为6的长方形,若将长方形的宽增加 , 长不变,则增加的长方形的面积y与x之间的关系式为( )A、 B、 C、 D、6. 某商场为了吸引顾客,设计了如图所示的可自由转动的转盘,当指针指向阴影部分时,顾客可获得一份奖品,那么顾客获奖的概率为( )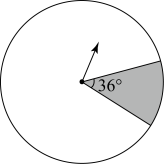 A、 B、 C、 D、7. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
A、 B、 C、 D、7. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )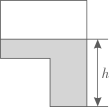 A、
A、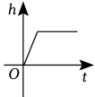 B、
B、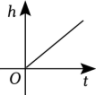 C、
C、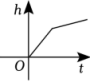 D、
D、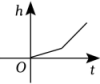 8. 如图,在中, , 平分 , 交于点 . 若 , 则( )
8. 如图,在中, , 平分 , 交于点 . 若 , 则( )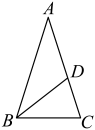 A、 B、 C、 D、9. 如图,在边长为1的小正方形网格中,P为上任一点,的值为( )
A、 B、 C、 D、9. 如图,在边长为1的小正方形网格中,P为上任一点,的值为( )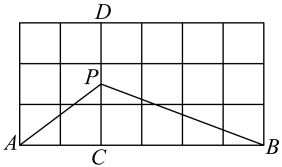 A、6 B、8 C、10 D、1210. 设 , , . 若 , 则的值是( )A、5 B、6 C、7 D、8
A、6 B、8 C、10 D、1210. 设 , , . 若 , 则的值是( )A、5 B、6 C、7 D、8二、填空题
-
11. 化简: .12. 一个等腰三角形的底角是顶角的倍,则这个三角形顶角的度数是 .13. 和睦社区一次歌唱比赛共500名选手参加,比赛分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),结合表中的信息,可得比赛分数在80~90分数段的选手有名.
分数段
60~70
70~80
80~90
90~100
频率
0.2
0.25
0.25
14. 如图所示是关于变量x , y的程序计算,若开始输入的x值为6,则最后输出因变量y的值为 .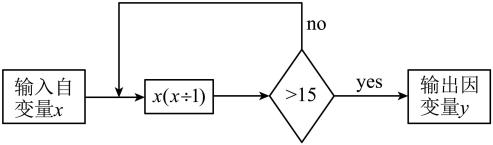 15. 中, , , 于D , E是边上任意一点,F是线段上任意一点,连接 , , 则的最小值是 .
15. 中, , , 于D , E是边上任意一点,F是线段上任意一点,连接 , , 则的最小值是 .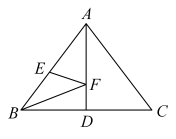 16. 如图,在中, , 分别以A、B为圆心,大于的长为半径画弧,两弧交于点M、N , 直线交于点D , 交的延长线于点E . 若 , , 则的长为 .
16. 如图,在中, , 分别以A、B为圆心,大于的长为半径画弧,两弧交于点M、N , 直线交于点D , 交的延长线于点E . 若 , , 则的长为 .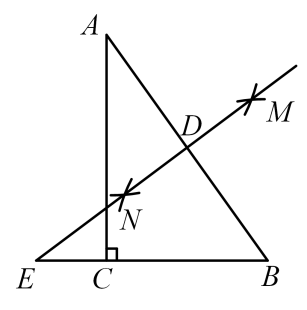
三、解答题
-
17. 计算题:(1)、;(2)、 .(3)、先化简,再求值: , 其中 .18. 如图, , , . 求证:平分 .
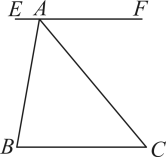 19. 某市出租车收费标准如下:3千米以内(含3千米)收费8元;超过3千米的部分每千米收费1.6元,当出租车行驶路程为x千米时,应收费为y元.(1)、请写出当时,y与x之间的关系式;(2)、小亮乘出租车行驶5千米,应付多少元?(3)、小亮付车费19.2元,出租车行驶了多少千米?20. 甲、乙二人做如下的游戏:从编号为1到20的卡片中任意抽出一张.(1)、若抽到的数字是奇数,则甲获胜,否则乙获胜.你认为这个游戏对甲、乙双方公平吗?(2)、若抽到的数字是3的倍数,则甲获胜;若抽到的数字是5的倍数,则乙获胜,你认为这个游戏对甲、乙双方公平吗?21. 如图, , , .请写出 与 的数量关系,并证明你的结论.
19. 某市出租车收费标准如下:3千米以内(含3千米)收费8元;超过3千米的部分每千米收费1.6元,当出租车行驶路程为x千米时,应收费为y元.(1)、请写出当时,y与x之间的关系式;(2)、小亮乘出租车行驶5千米,应付多少元?(3)、小亮付车费19.2元,出租车行驶了多少千米?20. 甲、乙二人做如下的游戏:从编号为1到20的卡片中任意抽出一张.(1)、若抽到的数字是奇数,则甲获胜,否则乙获胜.你认为这个游戏对甲、乙双方公平吗?(2)、若抽到的数字是3的倍数,则甲获胜;若抽到的数字是5的倍数,则乙获胜,你认为这个游戏对甲、乙双方公平吗?21. 如图, , , .请写出 与 的数量关系,并证明你的结论. 22. 如图,在正方形网格上有一个△ABC,三个顶点都在格点上,网格上的最小正方形的边长为1.
22. 如图,在正方形网格上有一个△ABC,三个顶点都在格点上,网格上的最小正方形的边长为1.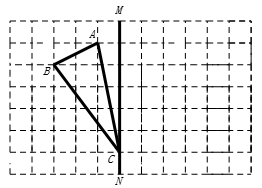 (1)、作△ABC关于直线MN的对称图形△A′B′C′(不写作法);(2)、求BC的长;(3)、求△ABC的面积.23. 如图,在正方形ABCD中, , , , 图中有几个直角三角形?你是如何判断的?与同伴进行交流.
(1)、作△ABC关于直线MN的对称图形△A′B′C′(不写作法);(2)、求BC的长;(3)、求△ABC的面积.23. 如图,在正方形ABCD中, , , , 图中有几个直角三角形?你是如何判断的?与同伴进行交流.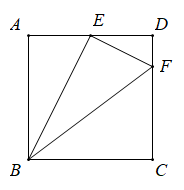 24. 如图(1)是一个长为 , 宽为的长方形,沿图中的虚线剪开,平均分成四个小长方形,然后按图(2)形状拼成一个正方形.
24. 如图(1)是一个长为 , 宽为的长方形,沿图中的虚线剪开,平均分成四个小长方形,然后按图(2)形状拼成一个正方形.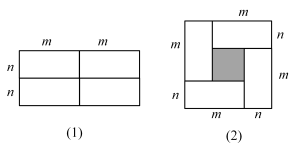 (1)、图(2)中的阴影部分的正方形边长是(用含m,n的式子表示)(2)、请用两种不同的方法求图(2)阴影部分的面积;(3)、观察图(2),请你写出 , , 之间的等量关系是:(4)、根据(3)题中的等量关系,解决下列问题:若 , , 求的值.25. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的关系,根据图象,解答下列问题:
(1)、图(2)中的阴影部分的正方形边长是(用含m,n的式子表示)(2)、请用两种不同的方法求图(2)阴影部分的面积;(3)、观察图(2),请你写出 , , 之间的等量关系是:(4)、根据(3)题中的等量关系,解决下列问题:若 , , 求的值.25. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的关系,根据图象,解答下列问题: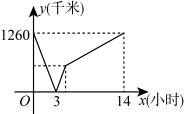 (1)、甲地与乙地相距千米,两车出发后小时相遇;(2)、普通列车到达终点共需小时,它的速度是千米/小时;(3)、求动车的速度;(4)、动车行驶多长时间与普通列车相距140千米?26. 中, , , 是直线上的一个动点,连接 , 过点作的垂线,垂足为点 , 过点作的平行线交直线于点 .
(1)、甲地与乙地相距千米,两车出发后小时相遇;(2)、普通列车到达终点共需小时,它的速度是千米/小时;(3)、求动车的速度;(4)、动车行驶多长时间与普通列车相距140千米?26. 中, , , 是直线上的一个动点,连接 , 过点作的垂线,垂足为点 , 过点作的平行线交直线于点 .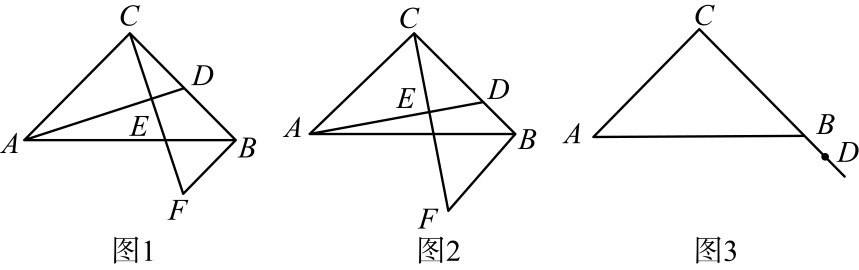 (1)、如图1,当点为中点时,请直接写出线段与的数量关系.(2)、如图2,当点在线段上不与 , 重合 , 请探究线段 , , 之间的数量关系(要求:写出发现的结论,并说明理由).(3)、如图3,当点在线段延长线上,请探究线段 , , 之间的数量关系(要求:画出图形,写出发现的结论,并说明理由).(4)、当点在线段延长线上,请直接写出线段 , , 之间的数量关系.
(1)、如图1,当点为中点时,请直接写出线段与的数量关系.(2)、如图2,当点在线段上不与 , 重合 , 请探究线段 , , 之间的数量关系(要求:写出发现的结论,并说明理由).(3)、如图3,当点在线段延长线上,请探究线段 , , 之间的数量关系(要求:画出图形,写出发现的结论,并说明理由).(4)、当点在线段延长线上,请直接写出线段 , , 之间的数量关系.