山东省青岛市崂山区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 我们用肥皂水可以吹出漂亮的泡泡,其泡沫的厚度约0.000326毫米,数字0.000326用科学记数法表示为( )A、 B、 C、 D、2. 如图, , , 平分 , 则为( )
 A、 B、 C、 D、3. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
A、 B、 C、 D、3. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )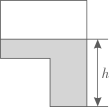 A、
A、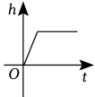 B、
B、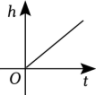 C、
C、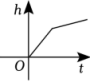 D、
D、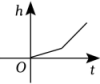 4. 以下是四届冬奥会会标的一部分,其中是轴对称图形的是( )A、
4. 以下是四届冬奥会会标的一部分,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出3个球,下列事件是必然事件的是( )A、至少有一个黑球 B、至少有一个白球 C、至少有两个黑球 D、至少有两个白球6. 把两块三角板按如图所示那样拼在一起,的大小为( )
5. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出3个球,下列事件是必然事件的是( )A、至少有一个黑球 B、至少有一个白球 C、至少有两个黑球 D、至少有两个白球6. 把两块三角板按如图所示那样拼在一起,的大小为( ) A、 B、 C、 D、7. 如图,斑马线的作用是为了引导行人安全地通过马路,小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A、 B、 C、 D、7. 如图,斑马线的作用是为了引导行人安全地通过马路,小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )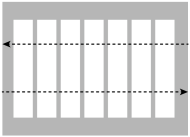 A、垂线段最短 B、过直线外一点有且只有一条直线与已知直线平行 C、两点确定一条直线 D、两点之间,线段最短8. 如图,由作图痕迹做出如下判断,其中正确的是( )
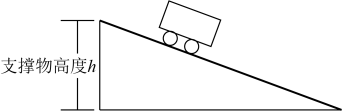
A、垂线段最短 B、过直线外一点有且只有一条直线与已知直线平行 C、两点确定一条直线 D、两点之间,线段最短8. 如图,由作图痕迹做出如下判断,其中正确的是( ) A、 B、 C、 D、9. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )
A、 B、 C、 D、9. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )木板的支撑物高度
…
下滑时间
…
 A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短10. 乐乐所在的七年级某班学生到野外活动,为测量一池塘两端A , B的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:
A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短10. 乐乐所在的七年级某班学生到野外活动,为测量一池塘两端A , B的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:乐乐:如图①,先在平地取一个可直接到达A , B的点C , 再连接AC , BC , 并分别延长AC至D , BC至E ,
使 , , 最后测出DE的长即为A , B的距离.
明明:加图②,先过点B作AB的垂线BF , 再在BF上取C , D两点,使 , 接看过点D作BD的垂线DE , 交AC的延长线于点E , 则测出DE的长即为A , B的距离.
聪聪:如图③,过点B作BD⊥AB , 再由点D观测,在AB的延长线上取一点C , 使 , 这时只要测出BC的长即为A , B的距离.
以上三位同学所设计的方案中可行的是( )
 A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行
A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行二、填空题
-
11. 计算 .12. 如果关于 的多项式 是一个完全平方式,那么13. 如图,已知 , 点D为内部的一点,以D为顶点,作 , 使得 , , 则得到的 .
 14. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD=° .
14. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD=° . 15. 如图,点E , F在上, , , 请你添加一个条件(不添加字母和辅助线),使得≌ , 你添加的条件是 .
15. 如图,点E , F在上, , , 请你添加一个条件(不添加字母和辅助线),使得≌ , 你添加的条件是 . 16. 如图,直线 , 点A在直线上,以点A为圆心,适当长度为半径画弧,分别交直线 , 于B , C两点,以点C为圆心,长为半径画弧,与前弧交于点D(不与点B重合),连接 , , , , 其中交于点E . 若 , 则下列结论正确的是 . (只填序号)
16. 如图,直线 , 点A在直线上,以点A为圆心,适当长度为半径画弧,分别交直线 , 于B , C两点,以点C为圆心,长为半径画弧,与前弧交于点D(不与点B重合),连接 , , , , 其中交于点E . 若 , 则下列结论正确的是 . (只填序号)①;②;③;④;⑤若 , 则与的周长差1.5.

三、解答题
-
17. 计算(1)、;(2)、;(3)、;(4)、 .18. 先化简,再求值: , 其中 .19. 某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
 (1)、甲顾客消费150元,求获得打折待遇的概率;(2)、乙顾客消费120元,求获得五折待遇的概率.20. 如图,已知点E、F在直线上,点G在线段上,与交于点H , , .
(1)、甲顾客消费150元,求获得打折待遇的概率;(2)、乙顾客消费120元,求获得五折待遇的概率.20. 如图,已知点E、F在直线上,点G在线段上,与交于点H , , . (1)、试判断与之间的数量关系,并说明理由;(2)、若 , , 求的度数.21. 证明:三角形内角和180°(画图,写已知、求证,并完成证明)
(1)、试判断与之间的数量关系,并说明理由;(2)、若 , , 求的度数.21. 证明:三角形内角和180°(画图,写已知、求证,并完成证明)已知:
求证:
证明:
22. 如图所示,梯形上底的长是x , 下底的长是14,高是6 (1)、求梯形面积y与上底长x之间的关系式;(2)、用表格表示当x每次增加1,从4变到13时,y的相应值;(3)、当x每增加1时,y如何变化?说说你的理由;(4)、当时,y等于什么?此时它表示的是什么?23. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , .
(1)、求梯形面积y与上底长x之间的关系式;(2)、用表格表示当x每次增加1,从4变到13时,y的相应值;(3)、当x每增加1时,y如何变化?说说你的理由;(4)、当时,y等于什么?此时它表示的是什么?23. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , . (1)、【发现问题】
(1)、【发现问题】如图①,当 , 时,则与的数量关系是 .
(2)、【探究问题】如图②,点C , D在射线 , 上滑动,且 , 当时,与在【发现问题】中的数量关系还成立吗?说明理由.

