山东省青岛市市北区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下面是青岛、济南、郑州、太原四个城市的地铁图标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件属于必然事件的是（）

A、随机掷一枚质地均匀的骰子一次，掷出的点数是1 B、车辆随机经过一个路口，遇到红灯 C、任意画一个三角形，其内角和是 $180 °$ D、有三条线段，将这三条线段首尾顺次相接可以组成一个三角形

查看试题解析
3. 下列各式，正确的是（）

A、 $3 a - a = 2$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{6} \div 2 a^{2} = \frac{1}{2} a^{4}$ D、 $1.2 5^{2019} \times {(- \frac{4}{5})}^{2021} = 1$

查看试题解析
4. 如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（　　）

A、 $\frac{5}{9}$ B、 $\frac{1}{3}$ C、 $\frac{5}{18}$ D、 $\frac{2}{3}$

查看试题解析
5. 如图，某海域中有A ， B ， C三个小岛，其中C在A的北偏东 $70 °$ 方向，C在B的南偏东 $35 °$ 方向，B ， C到A的距离相等，则小岛A相对于小岛B的方向是（）

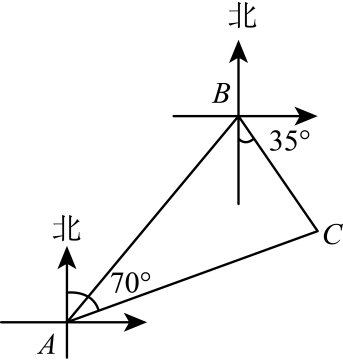A、北偏东 $70 °$ B、北偏东 $40 °$ C、南偏西 $40 °$ D、南偏西 $35 °$

查看试题解析
6. 剪纸是我国传统的民间艺术．将一张纸片按图中①，②的方式沿虚线依次对折后，再沿图③中的虚线裁剪，最后将图④中的纸片打开铺平，所得图案应该是（）

A、 B、 C、 D、

查看试题解析
7. 如图，一个等腰直角三角形零件放置在一凹槽内，顶点 $A$ 、 $B$ 、 $C$ 分别落在凹槽内壁上，测得 $A D = 5 c m$ ， $B E = 9 c m$ ，则该零件的面积为（）

A、14 B、53 C、98 D、196

查看试题解析

二、填空题

8. 如图，一扇窗户打开后，用窗钩 $B C$ 可将其固定，这所运用的是三角形的．

查看试题解析
9. 冠状病毒因在显微镜下观察类似王冠而得名，新型冠状病毒是以前从未在人体中发现的冠状病毒，新型冠状病毒的半径约是0.000000045米，将数0.000000045用科学记数法表示为．

查看试题解析
10. 如图， $∠ l = ∠ 2$ ，现要添加一个条件使 $△ A B D ≌ △ A C D$ ，可以添加．（只添一个即可）．

查看试题解析
11. 根据如图所示的程序，当输入 $x = - 1$ 时，输出的结果y是．

查看试题解析
12. 满足条件 $∠ A = 2 ∠ B = 2 ∠ C$ 的 $△ A B C$ ，它最大的角的度数是，因此这是一个三角形．

查看试题解析

13. 林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组统计数据：

移植的棵数n	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数m	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

估计该种幼树在此条件下移植成活的概率为．（精确到0.01）

查看试题解析

14. 如图，在 $△ A B C$ 中， $∠ C = 9 0^{°}$ ，以A为圆心，任意长为半径画弧，分别交 $A C$ ， $A B$ 于点M ， N ，再分别以M ， N为圆心，大于 $\frac{1}{2} M N$ 长为半径画弧，两弧交于点O ，作射线 $A O$ ，交 $B C$ 于点E ，已知 $A B = 10$ ， $S_{△ A B E} = 20$ ，则 $C E$ 的长为．

查看试题解析
15. 如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB=65°，则∠AED′等于°．

查看试题解析

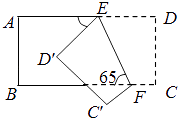
三、解答题

16.

(1)、下面的方格图是由边长为1的42个小正方形拼成的， $△ A B C$ 的顶点A、B、C均在小正方形的顶点上．
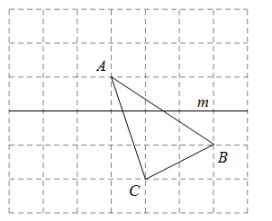
①作出 $△ A B C$ 关于直线m轴对称的 $△ A_{1} B_{1} C_{1}$ ；
② $△ A B C$ 的面积 $=$ ．

(2)、请仅用直尺和圆规，按要求完成画图，不写做法，但要保留作图痕迹．

已知： $△ A B C$ 如图所示．

求作： $△ D E F$ ，使 $△ A B C ≌ △ D E F$ ．

查看试题解析
17. 计算：

(1)、 $| - 2 | - {(2 - π)}^{0} + {(- \frac{1}{3})}^{- 1}$ ；

(2)、 $(- 3 x) \cdot {(- \frac{2}{3} x^{2} y)}^{3} \div (- \frac{3}{4} y^{3} x^{5})$ ；

(3)、利用完全平方公式计算 $9 9^{2}$ ；

(4)、 $3 x (2 x + 5) - (x - 2) (5 x + 1)$ ；

(5)、先化简，再求值： $(a + 2 b) (a - 2 b) - {(2 a + b)}^{2}$ ，其中 $a = - 1$ ， $b = 2$ ．

查看试题解析
18. 小亮和小芳都想参加学校社团组织的暑假实践活动，但只有一个名额，小亮提议用如下的办法决定谁去参加活动；将一个均匀的、可以自由转动的转盘9等分，分别标上1至9九个号码，随机转动转盘，若转到3的倍数，小亮去参加活动；转到偶数，小芳去参加活动；转到其它号码则重新转动转盘．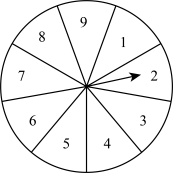

(1)、转盘转到3的倍数的概率是多少？

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析
19. 如图，已知： $∠ A = ∠ F$ ， $C E ∥ B D$ ，请根据图形填空，并在括号内注明理由．

查看试题解析

20. 某公交车每月的支出费用为4000元，每月的乘车人数x(人)与每月利润(利润＝收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的)：

x(人)	500	1000	1500	2000	2500	3000	…
y(元)	﹣3000	﹣2000	﹣1000	0	1000	2000	…

(1)、在这个变化过程中，是自变量，是因变量；

(2)、观察表中数据可知，每月乘客量达到人以上时，该公交车才不会亏损；

(3)、请你估计当每月乘车人数为3500人时，每月利润为多少元？

查看试题解析

21. 为了解学生对所学知识的应用能力，某校老师在七年级数学兴趣小组活动中，设置了这样的问题：因为池塘两端A ， B的距离无法直接测量，请同学们设计方案测量A ， B的距离．甲、乙两位同学分别设计出了如下两种方案：
甲：如图1，在平地上取一个可以直接到达点A ， B的点O ，连接 $A O$ 并延长到点C ，连接 $B O$ 并延长到点D ，使 $C O = A O$ ， $D O = B O$ ．连接 $D C$ ，测出 $D C$ 的长即可．
乙：如图2，先确定直线 $A B$ ，过点B作直线 $B E$ ，在直线 $B E$ 上找可以直接到达点A的一点D ，连接 $D A$ ，作 $∠ A D B = ∠ B D C$ ，交直线 $A B$ 于点C ，最后测量 $B C$ 的长即可．

(1)、甲、乙两同学的方案哪个可行？

(2)、请说明你认为方案可行的理由：
以上的生活情景化归到数学上：根据题意，此时，
已知条件是：；有待说明的是：；
请介绍你每一步的思考及相应的道理：

(3)、请将不可行的方案稍加修改使之可行．
你的修改是：

查看试题解析
22. 为了加强居民的节水意识，合理利用水资源，某高档小区对直饮水采用价格调控手段以期待达到节水的目的，下图是此小区对居民直饮水某月用水量 $x$ 吨与水费 $y$ 元的函数图象（水费按月结算）．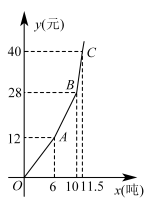

(1)、填空：
价格表
每月水用量
单价
不超出 $6$ 吨的部分
超出 $6$ 吨不超出 $10$ 吨的部分
▲  元/吨
     ▲  元/吨
超出 $10$ 吨的部分
     ▲  元/吨

(2)、若某户居民 $9$ 月份用水量为 $9.5$ 吨，求该用户 $9$ 月份水费；

(3)、若某户居民 $11$ 月用水 $a$ （吨），用含 $a$ 的代数式表示该户居民 $11$ 月共应交水费 $Q$ （元）．

查看试题解析
23.

(1)、探究（一）
如图①，为了支持山庄经济开发，政府派出免费车为山庄A和山庄B向山外运农产品，免费车只能在公路l上行驶，你认为停在哪里，到两村庄距离相等？
请通过尺规作图表达你的观点．

(2)、探究（二）
如图②，为了支持山庄经济开发，政府派出免费车为山庄A和山庄B向山外运农产品，免费车只能在公路l上行驶，你认为停在哪里，到两村庄距离和最短？请借助刻度尺、直角三角板或圆规等，通过画图表达你的观点；也可以文字叙述你的做法．

(3)、探究（三）
如图③，为了支持山庄经济开发，政府派出免费车为山庄A和山庄B向山外运农产品，免费车只能在公路l上行驶，你认为停在哪里， $| P A - P B |$ 最大？
请借助刻度尺、直角三角板或圆规等，通过画图表达你的观点；也可以文字叙述你的做法．

(4)、拓展应用
如图④， $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B A C = 60 °$ ， $B C = 6$ ， E是 $A B$ 的中点，P是 $B C$ 边上的一动点，则 $P A + P E$ 的最小值为 ▲ ；

查看试题解析

价格表
每月水用量	单价
不超出 $6$ 吨的部分超出 $6$ 吨不超出 $10$ 吨的部分	▲ 元/吨 ▲ 元/吨
超出 $10$ 吨的部分	▲ 元/吨