山东省青岛市市南区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 C、x+3>y+3 D、-3x>-3y2. 我国将在2060年实现碳中和,新能源、绿色能源将成为产业发展的新趋势,下列新能源环保图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列变形中,是因式分解且正确的是( )A、 B、 C、 D、4. 如图,中, , 的垂直平分线分别交 , 于点D , E , 则线段的长为( )
3. 下列变形中,是因式分解且正确的是( )A、 B、 C、 D、4. 如图,中, , 的垂直平分线分别交 , 于点D , E , 则线段的长为( ) A、 B、2 C、 D、5. 如图,由一个正六边形和正五边形组成的图形中,的度数应是( )
A、 B、2 C、 D、5. 如图,由一个正六边形和正五边形组成的图形中,的度数应是( ) A、 B、 C、 D、6. 若关于x的不等式组无解,则a的取值范围是( )A、 B、 C、 D、7. 甲、乙两人同时从A地出发到B地,如果甲的速度v保持不变,而乙先用v的速度到达中点,再用2v的速度到达B地,则下列结论中正确的是( )A、甲、乙同时到达B地 B、甲先到达B地 C、乙先到达B地 D、谁先到达B地与v有关8. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF;④S△AEF . 其中正确的有( )
A、 B、 C、 D、6. 若关于x的不等式组无解,则a的取值范围是( )A、 B、 C、 D、7. 甲、乙两人同时从A地出发到B地,如果甲的速度v保持不变,而乙先用v的速度到达中点,再用2v的速度到达B地,则下列结论中正确的是( )A、甲、乙同时到达B地 B、甲先到达B地 C、乙先到达B地 D、谁先到达B地与v有关8. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF;④S△AEF . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 分解因式: .10. 等腰三角形的一个角100°,它的另外两个角的度数分别为11. 用等边三角形和正方形作平面镶嵌,则在它的每个顶点周围有个等边三角形和 个正方形.12. 如图,直线与直线相交于点A , 则关于x的不等式的解集为 .
 13. 如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n(以上长度单位:cm).观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为
13. 如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n(以上长度单位:cm).观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 14. 已知关于的分式方程的解为负数,则的取值范围是 .15. 在中,的平分线与的延长线交于点 , 与交于点 . 若点为的中点,于 , 且 , , 则的长为 .
14. 已知关于的分式方程的解为负数,则的取值范围是 .15. 在中,的平分线与的延长线交于点 , 与交于点 . 若点为的中点,于 , 且 , , 则的长为 .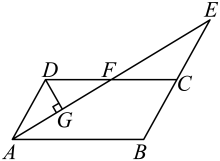 16. 如图,矩形的边 , E是上一点, , F是上一动点,M、N分别是的中点,则的最小值是 .
16. 如图,矩形的边 , E是上一点, , F是上一动点,M、N分别是的中点,则的最小值是 .
三、解答题
-
17. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.

已知: ,
求作: , 使得在边上,且它到、两边的距离相等.
18.(1)、因式分解:;(2)、化简:;(3)、解不等式组: , 并把解集在数轴上表示出来;(4)、解方程: .19. 在长度均为1的正方形网格中建立如图所示的平面直角坐标系,已知点A、B、C的坐标分别为 . (1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .20. 如图,中, , , 点F为延长线上一点,点E在上,且 .
(1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .20. 如图,中, , , 点F为延长线上一点,点E在上,且 . (1)、求证:;(2)、若 , 求的度数.21. 【调查活动】
(1)、求证:;(2)、若 , 求的度数.21. 【调查活动】小峰同学为了完成老师布置的社会活动作业:《A市初中生阅读水平的现状》,随机走访了A市的甲、乙两所初中,收集到如下信息:
①甲、乙两校图书室各藏书18000册;
②甲校比乙校人均图书册数多2册;
③甲校的学生人数比乙校的人数少10%.
【问题解决】
请你根据上述三个信息,就甲、乙两校的“人数”或“人均图书册数”提出一个用分式方程解决的问题,并写出解题过程.
22. 已知如图,在中,点E , F在对角线AC上,且 . 求证: (1)、;(2)、四边形是平行四边形.23. 某校组织元旦汇演,准备购进 , 两种文具共40件作为奖品,设购进种文具件,总费用为元. , 文具的费用与的函数关系如下表.
(1)、;(2)、四边形是平行四边形.23. 某校组织元旦汇演,准备购进 , 两种文具共40件作为奖品,设购进种文具件,总费用为元. , 文具的费用与的函数关系如下表.(件)
8
9
12
种文具费用(元)
120
135
▲
种文具费用(元)
640
▲
560
(1)、将表格补充完整.(2)、求关于的函数表达式.(3)、当种文具的费用不大于种文具的费用时,求总费用的最小值.24. 在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是D , E . (1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.25. 如图,在平面直角坐标系中,直线与x轴、y轴相交于A、B两点,动点C在线段上,将线段绕着点C顺时针旋转得到 , 此时点D恰好落在直线上时,过点D作轴于点E .
(1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.25. 如图,在平面直角坐标系中,直线与x轴、y轴相交于A、B两点,动点C在线段上,将线段绕着点C顺时针旋转得到 , 此时点D恰好落在直线上时,过点D作轴于点E .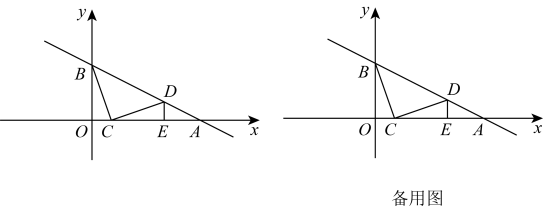 (1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.
(1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.