山东省青岛市市南区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 地铁作为城市的重要骨干交通,具有节省土地、节约资源、减少污染、快捷安全、舒适方便等特点,下列地铁标志中是轴对称图形的是( )A、济南
 B、太原
B、太原 C、青岛
C、青岛 D、郑州
D、郑州 2. 下列计算正确的是( )A、 B、 C、 D、3. 已知 , 将含角的直角三角板如图放置,若 , 则的度数为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 已知 , 将含角的直角三角板如图放置,若 , 则的度数为( )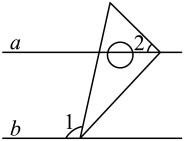 A、 B、 C、 D、4. 小华有两根长度为的木棒,他想摆一个三角形木框摆件,现有、和五根木棒供他选择,则小华可选择的方式有( )A、1种 B、2种 C、3种 D、4种5. 如图是一个简单的数值运算程序,当输入的值为5时,输出的结果为( )
A、 B、 C、 D、4. 小华有两根长度为的木棒,他想摆一个三角形木框摆件,现有、和五根木棒供他选择,则小华可选择的方式有( )A、1种 B、2种 C、3种 D、4种5. 如图是一个简单的数值运算程序,当输入的值为5时,输出的结果为( ) A、10 B、12 C、132 D、3806. 兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑的慢,就停下来看风景.过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用分别表示弟弟和哥哥所跑的路程,t为跑步时间,则下列图象中与故事情节相吻合的是( )A、
A、10 B、12 C、132 D、3806. 兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑的慢,就停下来看风景.过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用分别表示弟弟和哥哥所跑的路程,t为跑步时间,则下列图象中与故事情节相吻合的是( )A、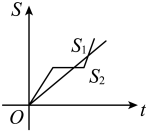 B、
B、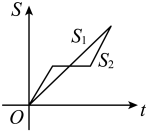 C、
C、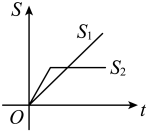 D、
D、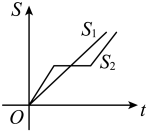 7. 下列事件中,判断正确有( )
7. 下列事件中,判断正确有( )①在地球上抛出的篮球会下落,是必然事件;
②郑一枚图钉,针尖朝上,是不可能事件;
③从一副扑克牌(含大小王)中抽一张,恰好是黑桃5,是随机事件;
④若 , 则一定有 , 是必然事件.
A、1个 B、2个 C、3个 D、4个8. 如图,在中,是三个内角平分线的交点,若面积为 , 且到边的距离为 , 则的周长为( )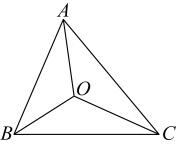 A、 B、 C、 D、9. 如图,王华站在河边的处,在河对面(王华的正北方向)的处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了步到达电线杆处,接着再向前走了步到达处,然后转向正南方向直行,当他看到电线塔、电线杆与所处位置在一条直线上时,他共计走了步.若王华步长约为米,则处与电线塔的距离约为( )
A、 B、 C、 D、9. 如图,王华站在河边的处,在河对面(王华的正北方向)的处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了步到达电线杆处,接着再向前走了步到达处,然后转向正南方向直行,当他看到电线塔、电线杆与所处位置在一条直线上时,他共计走了步.若王华步长约为米,则处与电线塔的距离约为( )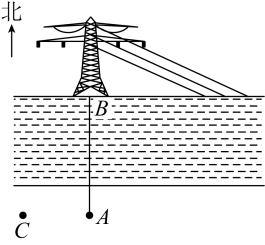 A、米 B、米 C、米 D、米10. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )
A、米 B、米 C、米 D、米10. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )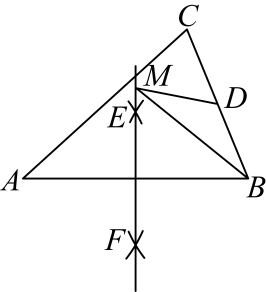 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 近几年我国芯片产业出现被卡脖子的情况,其实中国半导体的芯片设计能力已经很强,主要问题和难点在制造环节,目前我国只能做到米的制造,用科学记数法将可表示为 .12. 计算: .13. 在一个不透明袋子里装有红球、黄球共16个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在左右,则袋子中黄球的个数大约是个.14. 如图所示的七巧板起源于我国先秦时期,由古算书《周髀算经》中关于正方形的分割术,经过历代演变而成,19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”).图2是由边长为2的正方形分割制作的七巧板拼摆而成的“叶问蹬”图,则图中拍起的“腿”(即阴影部分)的面积为 .
 15. 一房屋内部结构如图所示,小李在房屋内自由走动,则他停留在卧室或客厅的概率是 .
15. 一房屋内部结构如图所示,小李在房屋内自由走动,则他停留在卧室或客厅的概率是 .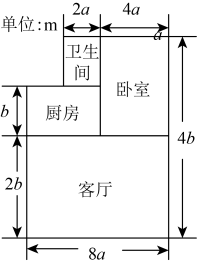 16. 如图,在中,是的角平分线,是上一点,连接 , 过点做 , 且的度数为 .
16. 如图,在中,是的角平分线,是上一点,连接 , 过点做 , 且的度数为 .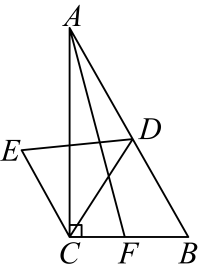
三、解答题
-
17. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.

已知: , 线段 .
求作: , 使 .
18.(1)、计算:;(2)、计算:;(3)、用简便方法计算:(4)、先化简,再求值 , 其中 .19. 下图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形,并画出对称轴.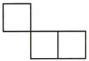

 20.(1)、材料一:甲、乙两个人做游戏:在一个不透明的口袋中装有张纸牌除数字外完全相同 , 它们分别标有数字 , , , , , , , , 从中随机摸出一张纸牌,若摸出纸牌上的数字是的倍数,则甲胜;若摸出纸牌上的数字是的倍数,则乙胜,请比较甲和乙谁获胜的概率大?
20.(1)、材料一:甲、乙两个人做游戏:在一个不透明的口袋中装有张纸牌除数字外完全相同 , 它们分别标有数字 , , , , , , , , 从中随机摸出一张纸牌,若摸出纸牌上的数字是的倍数,则甲胜;若摸出纸牌上的数字是的倍数,则乙胜,请比较甲和乙谁获胜的概率大?填 , =或
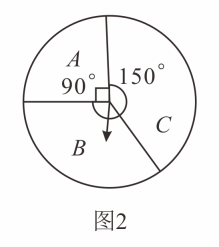
(2)、材料二:如图 , 某商场为吸引顾客,设立了一个可以自由转动的转盘转盘被等分成个扇形 , 并规定:顾客每购买元的商品,就能获得一次转动转盘的机会,若转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以分别获得元、元、元的购物券,则顾客转动一次转盘获得元购物券的概率是 .
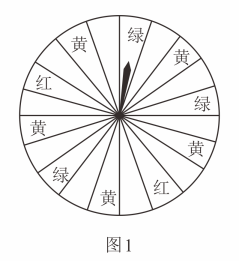 (3)、材料三:图是一个可以自由转动的转盘,转动转盘,停止后指针落在区域的概是 .
(3)、材料三:图是一个可以自由转动的转盘,转动转盘,停止后指针落在区域的概是 .
 21. 如图1,张老师将手机放在手机架上时,发现所形成的角度之间存在某些关系.如图2,分别是线段和上一点,且 , 请帮张老师求出与的度数和等于多少?
21. 如图1,张老师将手机放在手机架上时,发现所形成的角度之间存在某些关系.如图2,分别是线段和上一点,且 , 请帮张老师求出与的度数和等于多少?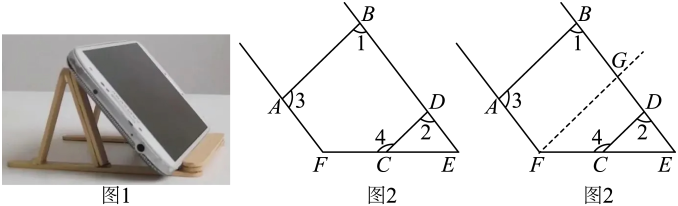
证明:过点作 , 交于点
∵(已知)
∴(① )
∵(已知)
∴②▲ (③ )
∴(④ )
∵(已作)
∴(⑤ )
∴(两直线平行,同旁内角互补)
∵(已作)
∴(两直线平行,同旁内角互补)
∴
∵
∴⑥▲
22. 如图1,甲、乙两人在跑道上进行折返跑,和是相邻的两条赛道(看成两条互相平行的线段),甲在赛道上以的速度从出发,到达后,以同样的速度返回 , 然后重复上述过程;乙在赛道上从出发,到达后以相同的速度回到 , 然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,乙到边的距离为与运动时间的函数图象如图2所示. (1)、赛道的长度是 , 乙的速度是;当时,甲、乙两人第一次相遇;(2)、当 ▲ 时,甲、乙两人第二次相遇?并求此时距离边多远?23. 如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)、赛道的长度是 , 乙的速度是;当时,甲、乙两人第一次相遇;(2)、当 ▲ 时,甲、乙两人第二次相遇?并求此时距离边多远?23. 如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.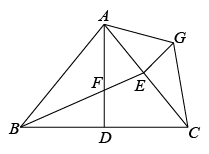 (1)、求证:△ABF≌△ACG;(2)、求证:BE=CG+EG.24. 日历上的数存在一定的规律,如下表是年月份的日历,我们设计这样的算法:任意选择其中的方框,将方框中的个数先各自平方,然后交叉求和,再相减.请你按照这个算法完成下列计算,并回答问题:
(1)、求证:△ABF≌△ACG;(2)、求证:BE=CG+EG.24. 日历上的数存在一定的规律,如下表是年月份的日历,我们设计这样的算法:任意选择其中的方框,将方框中的个数先各自平方,然后交叉求和,再相减.请你按照这个算法完成下列计算,并回答问题:年月份的日历
日
一
二
三
四
五
六
(1)、计算: , , 请任选一个方椐进行计算;(2)、通过计算你能发现什么规律,并请验证你的发现.25. 问题解决: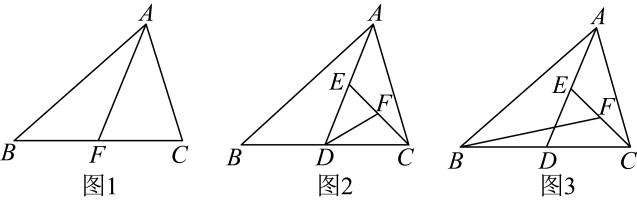
 (1)、如图1,中,为边上的中线,则 .
(1)、如图1,中,为边上的中线,则 .
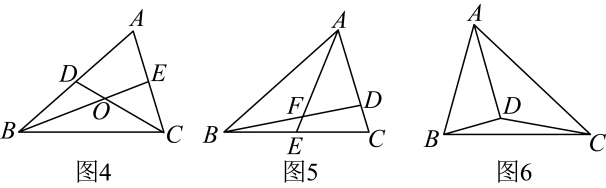
如图2,分别为的中点,则 .(2)、如图3,分别为的中点,若 , 则 .(3)、问题探究:如图4,是的中线,交于点与相等吗?解:中,由问题解决的结论可得, . ∴∴即 .
如图5,中,是上的一点,是的中线,且 , 试求的值.(4)、问题拓展:如图6,中,平分 , 则 .