山东省济南市高新区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 服饰文化是我国传统文化的重要组成部分．下列传统服饰图纹是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 盒子里有10个球，它们只有颜色不同，其中红球有7个，黄球有2个，黑球有1个．幸幸从中任意摸一个球，下面说法正确的是（）

A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小

查看试题解析
3. 若一个三角形的两边长分别为 $2 c m$ ， $7 c m$ ，则它的第三边的长可能是（）

A、 $2 c m$ B、 $3 c m$ C、 $6 c m$ D、 $9 c m$

查看试题解析
4. 李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）

A、金额 B、数量 C、单价 D、金额和单价

查看试题解析
5. 如图，点P是直线l外一点，且 $P C ⊥ l$ ，点C是垂足．点A，B，D在直线l上，下列线段中最短的是（）

A、 $P A$ B、 $P B$ C、 $P C$ D、 $P D$

查看试题解析
6. 下列运算中，正确的是（）

A、 $x^{3} \cdot x^{5} = x^{15}$ B、 $3 x + 2 x = 5 x^{2}$ C、 $x^{2} + y^{2} = x y^{4}$ D、 ${(- x^{4})}^{2} = x^{8}$

查看试题解析
7. 如图，四个全等的直角三角形围成一个大正方形ABCD ，中间阴影部分是一个小正方形EFGH ，这样就组成一个“赵爽弦图”，若AB=10，AE=8，则正方形EFGH的面积为（）

A、4 B、8 C、12 D、16

查看试题解析
8. 如图，直线 $a ∥ b ， ∠ 1 = 60 ° ， ∠ 2 = 100 °$ ，则 $∠ 3 =$ （）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $80 °$

查看试题解析
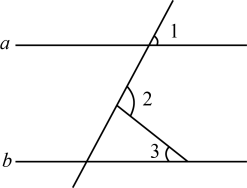9. 如图分割的正方形，拼接成长方形的方案中，可以验证（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b - b^{2}$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ B A C$ 的角平分线，若 $C D = 3$ ， $A B = 8$ ，则 $△ A B D$ 的面积是（）

A、24 B、12 C、15 D、10

查看试题解析
11. 如图，将长为 $8 c m$ 的橡皮筋放置在水平面上，固定两端A和B ，然后把中点C垂直向上拉升 $3 c m$ 至点D ，则橡皮筋被拉长了（）

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $6 c m$

查看试题解析
12. 要得知某一池塘两端A，B的距离，发现其无法直接测量，两同学提供了如下间接测量方案．
方案Ⅰ：如图1，先过点B作 $B F ⊥ A B$ ，再在 $B F$ 上取C，D两点，使 $B C = C D$ ，接着过点D作 $B D$ 的垂线 $D E$ ，交 $A C$ 的延长线于点E，则测量 $D E$ 的长即可；
方案Ⅱ：如图2，过点B作 $B D ⊥ A B$ ，再由点D观测，用测角仪在 $A B$ 的延长线上取一点C，使 $∠ B D C = ∠ B D A$ ，则测量 $B C$ 的长即可．
对于方案Ⅰ、Ⅱ，说法正确的是（）

A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行

查看试题解析

二、填空题

13. 计算： $- 20 m^{6} \div 5 m^{2} =$ ．

查看试题解析
14. 如图， $A D$ 是 $△ A B C$ 的中线， $M$ 是 $A C$ 边上的中点，连接 $D M$ ，若 $△ A B C$ 的面积为 $12 c m^{2}$ ，则 $△ A D M$ 的面积为 $c m^{2}$ ．

查看试题解析
15. 有一棵树苗，刚栽下去时树高为1.9米，以后每年长0.3米，则树高y（米）与年数x（年）之间的关系式为．

查看试题解析
16. 如图，把一张长方形纸片 $A B C D$ 沿 $E F$ 折叠后，D、C分别在M、N的位置上， $E M$ 与 $B C$ 的交点为G ，若 $∠ E F G = 65 °$ ，则 $∠ 2 =$ $°$ ．

查看试题解析
17. 如图，在下列网格中，小正方形的边长均为1，点 $A$ 、 $B$ 、 $O$ 都在格点上，则 $∠ A O B$ 的度数为．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C = 5 ， B C = 6$ ，线段 $A B ， A C$ 的垂直平分线交于点O ，则 $O A$ 的长度为．

查看试题解析

三、解答题

19. 计算： $x^{2} \cdot x^{5} + x \cdot x^{4} \cdot x^{2}$ ．

查看试题解析
20. 计算： $(x + 2) (2 x - 3)$ ．

查看试题解析
21. 如图是 $4 \times 4$ 正方形网格，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使整个涂成黑色的图形成为轴对称图形．请补全图形，并且画出对称轴（如图例），要求所画的四种方案不能重复．

查看试题解析
22. 如图， $A B ∥ C D$ ， $∠ 1 = 55 °$ ， $∠ D = ∠ C$ ，求 $∠ D$ ， $∠ C$ ， $∠ B$ 的度数．


解： $∵ A B ∥ C D$ ，

      $∴ ∠ D = ∠$      ▲  （两直线平行，同位角相等）．

      $∵ ∠ 1 = 55 °$ ，

      $∴ ∠ D =$      ▲   $°$ ，

      $∵ ∠ D = ∠ C$ ，

      $∴ ∠ C = ∠ 1 = 55 °$ ，

      $∵ A B ∥ C D$ ，

      $∴ ∠ B + ∠$      ▲   $= 180 °$ （  ）

      $∴ ∠ B =$      ▲  °

查看试题解析
23. 如图， $A D$ 是 $△ A B C$ 的角平分线， $A C = B C$ ， $∠ A D C = 60 °$ ，求 $∠ C$ 的度数．


解：令 $∠ B A D = x °$ ，

      $∵ A D$ 平分 $∠ B A C$ ，

      $∴ ∠ C A D = ∠ B A D = x °$ ， $∠ B A C =$     ▲  °（  ）

      $∵ A C = B C$ ，

      $∴ ∠ B = ∠ B A C$ （  ）

      $∴ ∠ B = 2 x °$ ．

$∵ ∠ A D C + ∠ A D B = 180 °$ ， $∠ A D B + ∠ B + ∠ B A D = 180 °$ ，

      $∴ ∠ A D C = ∠ B + ∠ B A D$ （  ）

      $∴ 2 x ° + x ° = 60 °$ ，得 $x = 20 °$ ，

      $∴ ∠ B = ∠ B A C = 40 °$ ．

在 $△ A B C$ 中，

      $∵ ∠ B A C + ∠ B + ∠ C = 180 °$

      $∴ ∠ C =$     ▲  °

查看试题解析
24. 先化简，再求值： ${(x - 3)}^{2} + (x + 2) (x - 2) + 3 x (2 - x)$ ，其中 $x = - 2$ ．

查看试题解析
25. 如图， $∠ A B C = ∠ D C B$ ， $A B = D C$ ， $A C = 5$ ，求 $B D$ 的长．

查看试题解析
26. 甲袋中有红球8个、白球5个和黑球12个；乙袋中有红球18个、白球9个和黑球23个．（每个球除颜色外都相同）

(1)、若从中任意摸出一个球是红球，选哪袋成功的机会大？请说明理由；

(2)、“从乙袋中取出10个红球后，乙袋中的红球个数和甲袋中红球个数一样多，所以此时若从中任意摸出一个球是红球，选甲、乙两袋成功的机会相同”．你认为这种说法正确吗？为什么？

查看试题解析
27. 如图，已知点 $D$ 在射线 $A E$ 上 $B D = C D$ ， $A E$ 平分 $∠ B A C$ 与 $∠ B D C$ ，求证 $A B = A C$ ．小明的证明过程如下：小明的证明是否正确？若正确，请在框内打“ $\sqrt$ ”，若错误，请写出你的证明过程．


证明：
          $∵ A E$ 平分 $∠ B A C$ ．
          $∴ ∠ B A D = ∠ C A D$ ．
          $∵ A D = A D$ ， $B D = C D$ ．
          $∴ △ A B D$ ≌ $△ A C D$
          $∴ A B = A C$ ．

查看试题解析

28. 安阳某初中数学小组欲测量吊车起重臂顶端与地面的距离，下面是他们设计的项目课题，请你根据下面的表格计算：吊车起重臂顶端

A

到地面的距离

A F

的长．

项目名称	测量吊车起重臂顶端与地面的距离
对象简介	吊车作业时是通过液压杆 $C D$ 的伸缩使起重臂 $A B$ 绕点 $B$ 转动的，从而使得起重臂升降作业 $. ($ 起重臂 $A B$ 的长度也可以伸缩 $)$
操作示意图
操作数据	起重臂 $A B = 10$ 米，点 $B$ 到地面的距离 $B E = 1.8$ 米，钢丝绳所在直线 $A F$ 垂直地面于点 $F$ ，点 $B$ 到 $A F$ 的距离 $B G = 8$ 米提示：四边形 $B E F G$ 是长方形， $B E = F G$ ．
操作评价

查看试题解析

29. 观察以下等式：
（x+1）（x²-x+1）=x³+1
（x+3）（x²-3x+9）=x³+27
（x+6）（x²-6x+36）=x³+216
…

(1)、按以上等式的规律，填空：（a+b）（ ▲ ）=a³+b³

(2)、利用多项式的乘法法则，说明（1）中的等式成立．

(3)、利用（1）中的公式化简：（x+y）（x²-xy+y²）-（x+2y）（x²-2xy+4y²）

查看试题解析
30. 在直线m上依次取互不重合的三个点D，A，E，在直线m上方有AB=AC，且满足∠BDA＝∠AEC＝∠BAC＝α.

(1)、如图1，当α=90°时，猜想线段DE，BD，CE之间的数量关系是；

(2)、如图2，当0°＜α＜180°时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；

(3)、拓展与应用：如图3，当α=120°时，点F为∠BAC平分线上的一点，且AB=AF，分别连接FB，FD，FE，FC，试判断△DEF的形状，并说明理由.

查看试题解析