四川省成都市武侯区重点学校2023-2024学年九年级上学期开学考试数学试卷
试卷更新日期:2023-09-27 类型:开学考试
一、
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、直角三角形 B、等边三角形 C、平行四边形 D、矩形2. 若线段 , , , 是成比例线段,且 , , ,则 ( )A、 B、 C、 D、3. 某多边形的内角和是其外角和的3倍,则此多边形的边数是( )A、5 B、6 C、7 D、84. 点在反比例函数的图象上,则下列各点在此函数图象上的是( )A、 B、 C、 D、5. 一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )A、 B、 C、 D、6. 下列说法中,正确的是( )A、四边相等的四边形是菱形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是菱形 D、对角线相等的平行四边形是菱形7. 如图,在正方形中,点分别在边和上, , 垂足为G,若 , 则的值为( )
 A、 B、 C、 D、8. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、40000009. 已知 , 则 .10. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是 .11. 如图,和是以点为位似中心的位似图形,相似比为: , 则和的面积比是 .
A、 B、 C、 D、8. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、40000009. 已知 , 则 .10. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是 .11. 如图,和是以点为位似中心的位似图形,相似比为: , 则和的面积比是 . 12. 现定义运算“★”,对于任意实数a,b, 都有a★ , 如:3★ ,若x★ ,则实数x的值是.13. 如图,正方形的对角线相交于点O,以O为顶点的正方形的两边 , 分别交正方形的边 , 于点M,N.记的面积为S1 , 的面积为S2 , 若正方形的边长 , S1=16,则S2的大小为 .
12. 现定义运算“★”,对于任意实数a,b, 都有a★ , 如:3★ ,若x★ ,则实数x的值是.13. 如图,正方形的对角线相交于点O,以O为顶点的正方形的两边 , 分别交正方形的边 , 于点M,N.记的面积为S1 , 的面积为S2 , 若正方形的边长 , S1=16,则S2的大小为 . 14.(1)、分解因式: .(2)、计算: .15. 解一元二次方程:(1)、(2)、16. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: )
14.(1)、分解因式: .(2)、计算: .15. 解一元二次方程:(1)、(2)、16. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: ) 17. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.
17. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.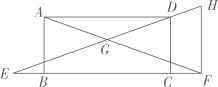 (1)、求证:.(2)、当时,求EF的长.18. 如图,一次函数的图象与反比例函数的图象交于点 .
(1)、求证:.(2)、当时,求EF的长.18. 如图,一次函数的图象与反比例函数的图象交于点 . (1)、求反比例函数与一次函数的表达式;(2)、若P为x轴上一点,的面积为5,求点P的坐标;(3)、结合图象,关于x的不等式的解集为 .19. 若a+b=3,a2+b2=7,则ab= .20. 关于x的一元二次方程 有两个不相等的实数根,则m的范围21. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为 .
(1)、求反比例函数与一次函数的表达式;(2)、若P为x轴上一点,的面积为5,求点P的坐标;(3)、结合图象,关于x的不等式的解集为 .19. 若a+b=3,a2+b2=7,则ab= .20. 关于x的一元二次方程 有两个不相等的实数根,则m的范围21. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为 . 22. 在矩形中, , , 如图所示折叠矩形纸片使点落在边上一点处,折痕端点、分别在边、上,则当折痕端点恰好与点重合时,的长为 .
22. 在矩形中, , , 如图所示折叠矩形纸片使点落在边上一点处,折痕端点、分别在边、上,则当折痕端点恰好与点重合时,的长为 . 23. 如图,矩形中, , , 是的中点,是线段上一动点,为的中点,连接 , 则线段的最小值为 .
23. 如图,矩形中, , , 是的中点,是线段上一动点,为的中点,连接 , 则线段的最小值为 . 24. 我校为了进行学雷锋爱心义卖活动,决定在操场划分一块面积为平方米的矩形场地若矩形场地的一边靠墙墙长米 , 另外三边由总长为米的围绳围成,并且在垂直于墙的边上各设置了一个开口宽为米的入口和出口如图请根据方案计算出矩形场地的边长各是多少米?
24. 我校为了进行学雷锋爱心义卖活动,决定在操场划分一块面积为平方米的矩形场地若矩形场地的一边靠墙墙长米 , 另外三边由总长为米的围绳围成,并且在垂直于墙的边上各设置了一个开口宽为米的入口和出口如图请根据方案计算出矩形场地的边长各是多少米?

