山东省青岛市崂山区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-27 类型:期末考试
一、单选题
-
1. 分式有意义的条件是( )A、 B、 C、 D、2. 已知 , 下列不等式中,变形正确的是( )A、 B、 C、 D、3. 以下分别是回收、节水、绿色包装、低碳4个标志,其中是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 4. 下列命题中,其逆命题为真命题的是( )A、内错角相等 B、若 , 则 C、对顶角相等 D、等腰三角形两底角相等5. 下列等式从左到右变形中,属于因式分解的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
4. 下列命题中,其逆命题为真命题的是( )A、内错角相等 B、若 , 则 C、对顶角相等 D、等腰三角形两底角相等5. 下列等式从左到右变形中,属于因式分解的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、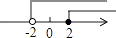 B、
B、 C、
C、 D、
D、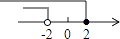 7. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且8. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
7. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且8. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( ) A、4,30° B、2,60° C、1,30° D、3,60°9. 《九章算术》中记录的一道题译为白话文是把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为 天,则可列方程为( )A、 B、 C、 D、10. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:
A、4,30° B、2,60° C、1,30° D、3,60°9. 《九章算术》中记录的一道题译为白话文是把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为 天,则可列方程为( )A、 B、 C、 D、10. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:①以点O为圆心,适当长为半径画弧,分别交 于点M , 交 于点N . ②分别以点M , N为圆心,大于 的长为半径画弧,两弧在 内相交于点E . ③画射线 ,交 于点 ,则点A的坐标为( )
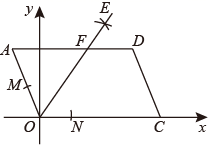 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
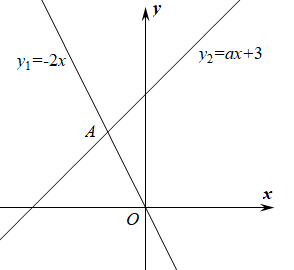
11. 因式分解:= .12. 若关于x的分式方程有增根,则m的值是 .13. 如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x≤ax+3的解集是 .
 14. 如图,在中, , 点为上一点,的垂直平分线交于点 , 将沿着折叠,点恰好和点重合,则的度数为 .
14. 如图,在中, , 点为上一点,的垂直平分线交于点 , 将沿着折叠,点恰好和点重合,则的度数为 . 15. 如图,将一个正八边形与一个正六边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠FEG= .
15. 如图,将一个正八边形与一个正六边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠FEG= .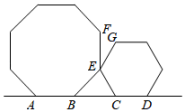 16. 如图,的对角线、交于点 , 平分交于点 , 且 , , 连接 . 下列结论:①;②;③;④ , 成立的有 . (把所有正确结论的序号都填在横线上)
16. 如图,的对角线、交于点 , 平分交于点 , 且 , , 连接 . 下列结论:①;②;③;④ , 成立的有 . (把所有正确结论的序号都填在横线上)
三、解答题
-
17. 已知点是边上一点.求作:点 , 使得 , 且点到两边的距离相等.(用尺规作图法,保留作图痕迹,不要求写作法)
 18. 在平面直角坐标系中,的位置如图,网格中小正方形边长为1,点A坐标为 , 请解答下列问题:
18. 在平面直角坐标系中,的位置如图,网格中小正方形边长为1,点A坐标为 , 请解答下列问题: (1)、作出绕点O的逆时针旋转得到的;(2)、计算的面积.19. 因式分解:(1)、;(2)、 .20.(1)、先化简,再求值: , 其中;(2)、解不等式组:21. 证明命题:如果两个锐角三角形有两边和其中一边上的高分别对应相等,那么这两个三角形全等.(1)、画出图形,写出已知,求证.(2)、写出证明过程.22. 某工厂生产、两种型号的扫地机器人.型机器人清扫所用的时间比型机器人多用50分钟.型机器人比型机器人每小时的清扫面积多 . 求型号扫地机器人每小时清扫面积是多少?23. 如图,的中线 , 相交于点G,点P,Q分别是 , 的中点.求证:
(1)、作出绕点O的逆时针旋转得到的;(2)、计算的面积.19. 因式分解:(1)、;(2)、 .20.(1)、先化简,再求值: , 其中;(2)、解不等式组:21. 证明命题:如果两个锐角三角形有两边和其中一边上的高分别对应相等,那么这两个三角形全等.(1)、画出图形,写出已知,求证.(2)、写出证明过程.22. 某工厂生产、两种型号的扫地机器人.型机器人清扫所用的时间比型机器人多用50分钟.型机器人比型机器人每小时的清扫面积多 . 求型号扫地机器人每小时清扫面积是多少?23. 如图,的中线 , 相交于点G,点P,Q分别是 , 的中点.求证: (1)、四边形是平行四边形;(2)、 .24. 零售经济成为社会关注的热门话题,小华从市场得知如下信息:
(1)、四边形是平行四边形;(2)、 .24. 零售经济成为社会关注的热门话题,小华从市场得知如下信息:甲商品
乙商品
进价(元/件)
65
5
售价(元/件)
90
10
小华计划购进甲、乙商品共100件进行销售,设小华购进甲商品x件.
(1)、小华用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围;(2)、在(1)的条件下,小华希望甲乙商品全部销售完后获得的利润不少于1450元,有哪些可行的进货方案?为获得最大利润,请你给出进货建议.25. 图形定义:四边形若满足 , 则我们称该四边形为“对角互补四边形”. (1)、若四边形为对角互补四边形,且 , 则的度数为 .(2)、如图1,四边形为对角互补四边形, . 求证:平分 .
(1)、若四边形为对角互补四边形,且 , 则的度数为 .(2)、如图1,四边形为对角互补四边形, . 求证:平分 .小云同学是这么做的:延长至 , 使得 , 连 , 可证明 , 得到是等腰直角三角形,由此证明出平分 , 还可以知道三者关系为: ;
(3)、如图2,四边形为对角互补四边形,且满足 , 则 , 三者关系为: .26. 如图,在平面直角坐标系中,是坐标原点,长方形的顶点分别在轴与轴上,已知 . 点为轴上一点,其坐标为 , 点从点出发以每秒2个单位的速度沿线段的方向运动,当点与点重合时停止运动,运动时间为秒. (1)、当点经过点时,求直线的函数解析式;(2)、求的面积关于的函数解析式;(3)、点在运动过程中是否存在使为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、当点经过点时,求直线的函数解析式;(2)、求的面积关于的函数解析式;(3)、点在运动过程中是否存在使为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由.