新疆阿克苏地区阿克苏市2023年中考数学二模试卷

试卷更新日期：2023-09-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共9小题，共45.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在 $- 3$ ， $2$ ， $- 2$ ， $0$ 四个数中，最小的数是（）

A、 $- 3$ B、 $1$ C、 $- 1$ D、 $0$

查看试题解析
2. 一个几何体的三视图如图所示，则这个几何体是（）

A、直三棱柱
B、直三棱锥
C、直四棱柱
D、直四棱锥

查看试题解析
3. 如图， $A B / / C D$ ，射线 $D F$ 交 $A B$ 于点 $E$ ， $∠ D = 70 °$ ，则 $∠ 1$ 的度数是（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
4. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $(- a^{3} b^{5})^{2} = a^{6} b^{10}$ C、 $2 a^{6} \div a^{2} = 2 a^{3}$ D、 $a^{2} \cdot a^{4} = a^{8}$

查看试题解析
5. 如图，数轴上的点A和点B分别在原点的左侧和右侧，点A、B对应的实数分别是a、b，下列结论一定成立的是（）

A、 $a + b < 0$ B、 $b - a < 0$ C、 $2 a > 2 b$ D、 $a + 2 < b + 2$

查看试题解析
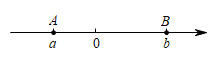6. 某班组织去看演出，甲种票每张 $26$ 元，乙种票每张 $20$ 元，如果 $38$ 名同学购票恰好用去 $952$ 元，甲乙两种票各买多少张？如果设甲种票买了 $x$ 张，乙种票买了 $y$ 张，那么根据题意，下列方程组中，正确的是（）

A、 ${\begin{array}{l} x - y = 38 \\ 26 x + 20 y = 952 \end{array}$ B、 ${\begin{array}{l} y - x = 38 \\ 20 x + 26 y = 952 \end{array}$
C、 ${\begin{array}{l} x + y = 38 \\ 26 x + 20 y = 952 \end{array}$ D、 ${\begin{array}{l} x + y = 38 \\ 20 x + 26 y = 952 \end{array}$

查看试题解析
7. 若 $x = 2$ 是方程 $x^{2} - x + m = 0$ 的一个根，则此方程的另一个根是（）

A、 $- 1$ B、 $0$ C、 $1$ D、 $2$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $A C = 4$ ， $∠ A B C = 90 °$ ， $B D$ 是 $△ A B C$ 的角平分线，过点 $D$ 作 $D E ⊥ B D$ 交 $B C$ 边于点 $E .$ 若 $A D = 1$ ，则图中阴影部分面积为（）

A、 $1$ B、 $1.5$ C、 $2$ D、 $2.5$

查看试题解析
9. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ， $∠ D = 90 °$ ， $A B = 4$ ， $B C = 6$ ， $∠ B A D = 30 ° .$ 动点 $P$ 沿路径 $A \to B \to C \to D$ 从点 $A$ 出发，以每秒 $1$ 个单位长度的速度向点 $D$ 运动．过点 $P$ 作 $P H ⊥ A D$ ，垂足为 $H .$ 设点 $P$ 运动的时间为 $x ($ 单位： $s)$ ， $△ A P H$ 的面积为 $y$ ，则 $y$ 关于 $x$ 的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共6小题，共30.0分）

10. 石墨烯是目前世界上最薄却最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.00000000034米，将这个数用科学记数法表示为．

查看试题解析
11. 外观相同的 $10$ 件产品中有两件不合格，现从中随机抽取一件进行检测，抽到不合格产品的概率为．

查看试题解析
12. 方程 $x^{2} - 9 = 0$ 的解是.

查看试题解析
13. 计算： $\frac{a^{2}}{a - 2} - \frac{4}{a - 2} =$ ．

查看试题解析
14. 一个圆锥的侧面积是底面积的2倍，则该圆锥的侧面展开图扇形的圆心角度数是度．

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A B = 8$ ， $E$ 是 $A B$ 的中点， $F$ 是 $B C$ 延长线上的点，将 $△ B E F$ 沿 $E F$ 折叠得到 $△ G E F$ ，连接 $B G$ 并延长分别交 $E F$ 、 $A D$ 于 $O$ 、 $H$ 两点，若 $G O = 3 G H$ ，则 $B F$ 的长度为．

查看试题解析

三、解答题（本大题共8小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

16. 计算： $(- 2)^{2} + \sqrt{8} - | 1 - \sqrt{2} | + (2023 - π)^{0}$ ．

查看试题解析
17. 解不等式组： ${\begin{array}{l} x - 1 < 3 ① \\ x + 1 \geq \frac{1 + 2 x}{3} ② \end{array}$ ．

查看试题解析
18. 已知：如图，在 $△ A B F$ 中， $∠ A B F = 90 °$ ， $A B$ 的垂直平分线 $C E$ 交 $A B$ 于点 $D$ ，交 $A F$ 于点 $C$ ，连接 $B E$ ， $B E = C F$ ．

(1)、求证： $△ A D C$ ≌ $△ B D E$ ；

(2)、若 $∠ C B F = 45 °$ ，四边形 $A E B C$ 是什么特殊平行四边形？请证明你的结论．

查看试题解析
19. 某中学为提升课后服务质量，决定设置“书法”“演讲”“绘画”“舞蹈”及“武术”五门校本课程，学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程（要求必须选修一门且只能选修一门）？”的随机问卷调查，并根据调查数据绘制了两幅不完整的统计图：

请结合上述信息，解答下列问题：

(1)、共有名学生参与了本次问卷调查；“演讲”在扇形统计图中所对应的圆心角是 °；

(2)、补全调查结果条形统计图；

(3)、小刚和小强分别从“书法”等五门校本课程中任选一门，请用列表法或画树状图法求出两人恰好选到同一门课程的概率．

查看试题解析
20. 某水果店购进甲、乙两种苹果的价格分别为8元/kg、12元/kg，这两种苹果的销售额y（单位：元）与销售量x（单位：kg）之间的关系如图所示．

(1)、写出图中点B表示的实际意义；

(2)、求乙种苹果销售额y与销售量x之间的函数解析式，并写出x的取值范围；

(3)、若不计损耗等因素，当甲、乙两种苹果的销售量均为akg时，它们的利润和为 $1500$ 元，求 $a$ 的值．

查看试题解析
21. 如图，海中有一个小岛 $A$ ，它周围 $10$ 海里内有暗礁，一艘渔船由西向东航行，在 $B$ 点测得小岛 $A$ 在北偏东 $60 °$ 方向上，航行 $8$ 海里到达 $D$ 点，这时测得小岛 $A$ 在北偏东 $45 °$ 方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？并说明理由 $. ($ 参考数据： $\sqrt{3} \approx 1.7)$

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径， $O C ⊥ A B$ ， $D E$ 与 $⊙ O$ 相切于点 $D$ ，弦 $C D$ 与 $O B$ 交于点 $F$ ，点 $E$ 在 $A B$ 的延长线上．

(1)、求 $∠ B D C$ 的度数；

(2)、求证： $E F = E D$ ；

(3)、若 $O F = 1 ， t a n A = \frac{1}{2}$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 如图所示，抛物线 $y = - x^{2} + 2 x + 3$ 的图象与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，连结 $B C$ ．

(1)、求抛物线顶点 $D$ 的坐标；

(2)、在直线 $B C$ 上方的抛物线上有一点 $M$ ，使得四边形 $A B M C$ 的面积最大，求点 $M$ 的坐标及四边形 $A B M C$ 面积的最大值；

(3)、点 $E$ 在抛物线上，当 $∠ E B C = ∠ A C O$ 时，直接写出点 $E$ 的坐标．

查看试题解析