新疆喀什地区2023中考二模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共9小题,共45.0分。在每小题列出的选项中,选出符合题目的一项)
-
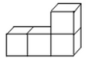
1. 下面四个数中最小的数是( )A、 B、 C、 D、2. 如图是由四个相同的小正方体搭成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各式中计算结果是的是( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、
3. 下列各式中计算结果是的是( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、 B、
B、
C、 D、
D、 5. 如图,直线 , 平分 , 若 , 则的度数是( )
5. 如图,直线 , 平分 , 若 , 则的度数是( ) A、 B、 C、 D、6. 关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根
A、 B、 C、 D、6. 关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、根的情况由的值决定7. 如图,的两直角边、分别在轴、轴上,已知 , , 将绕点顺时针方向旋转后得到 , 则点的坐标是( )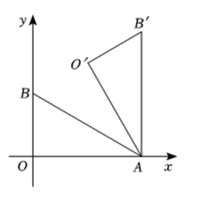 A、
A、
B、
C、
D、8. 某商品原价元,经过两次连续降价后为元,设平均每次降价的百分率为 , 则下面所列方程正确的是( )A、 B、
C、 D、9. 在某次千米跑步比赛中,甲、乙两名选手的行程随时间变化的图象如图所示,给出下列四个结论:起跑后小时内,甲在乙的前面:在第小时,两人都跑了千米;甲比乙先到达终点;甲在第小时跑了千米其中正确结论的个数有( )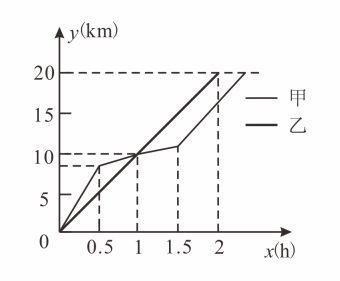 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本大题共6小题,共30.0分)
-
10. 二次根式 在实数范围内有意义,x的取值范围是.11. 一个多边形的内角和与它的外角和之比为 , 则这个多边形的边数是 .12. 在一个不透明的口袋里装有个除颜色外都完全相同的小球,其中红球有个,每次将袋子里的球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率稳定在 , 那么可以估算出的值为 .13. 如图,在平行四边形中,过点的直线 , 垂足为 , 若 , 则度.
 14. 某公路隧道的截面为圆弧形,设圆弧所在圆的圆心为 , 测得其同一水平线上、两点之间的距离为米,拱高为米,则的半径为 米
14. 某公路隧道的截面为圆弧形,设圆弧所在圆的圆心为 , 测得其同一水平线上、两点之间的距离为米,拱高为米,则的半径为 米 15. 如图,正方形的边长为 , 平分交于点 , 在上截取 , 连接 , 交于点 , 交于点 , 点是线段上一个动点,于点下列说法:≌;;;的最小值是正确的是 只填序号 .
15. 如图,正方形的边长为 , 平分交于点 , 在上截取 , 连接 , 交于点 , 交于点 , 点是线段上一个动点,于点下列说法:≌;;;的最小值是正确的是 只填序号 .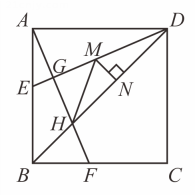
三、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
-
16. 计算: .17. 先化简,再求值: , 从 , , 中选择合适的的值代入求值.18. 如图,在中,是边上的中线,点是的中点,过点作交的延长线于 , 连接 .
 (1)、求证:≌;(2)、当 ▲ 时,四边形是菱形.19. 某校在暑假期间开展了“好书共读”活动,并随机抽取部分学生对活动期间的读书量进行调查,将调查所得数据进行了统计,并绘制了如下不完整的统计图和图 .
(1)、求证:≌;(2)、当 ▲ 时,四边形是菱形.19. 某校在暑假期间开展了“好书共读”活动,并随机抽取部分学生对活动期间的读书量进行调查,将调查所得数据进行了统计,并绘制了如下不完整的统计图和图 .
请根据相关信息,解答下列问题:
(1)、本次被调查的学生有 人;扇形统计图中 ;(2)、本次调查中读书量的众数是 本,中位数是 本,并补全条形统计图;(3)、若该校共有名学生,估计该校本次读书活动中读书量是本的学生有多少人.20. 某校数学兴趣小组的同学在教学楼顶端处测得实验楼顶部点的仰角为 , 已知两楼的间距为米,教学楼高为米图中所有点均在同一平面内 , 求实验楼的高度参考数据 , , 21. 如图,一次函数与反比例函数的图象相交于点、两点.
21. 如图,一次函数与反比例函数的图象相交于点、两点.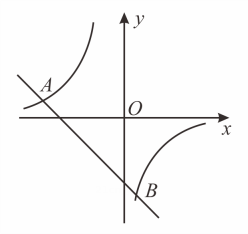 (1)、求一次函数的解析式;
(1)、求一次函数的解析式;
(2)、连接、 , 求的面积;(3)、当时,直接写出的取值范围.
