新疆生产建设兵团重点中学2023年中考一模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共9小题,共45.0分。在每小题列出的选项中,选出符合题目的一项)
-
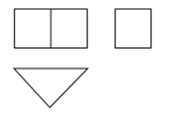
1. 的相反数是( )A、 B、 C、 D、2. 某几何体的主视图、左视图和俯视图如图所示,则其对应的几何体是( )
 A、
A、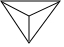 B、
B、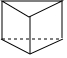 C、
C、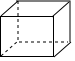 D、
D、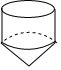 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是一款手推车的平面示意图,其中 , , , 则的大小是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是一款手推车的平面示意图,其中 , , , 则的大小是( ) A、
A、
B、
C、
D、5. 小明在计算一组数据的方差时,列出的公式如下 ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是6. 某中学八年级学生去距学校10千米的景点参观,一部分学生骑自行车先走,过了30分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为 千米/小时,则所列方程正确的是( )A、 B、 C、 D、7. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( ) A、 B、 C、 D、8. 如图,在四边形中, , , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 交于点若点是的中点,则的长为( )
A、 B、 C、 D、8. 如图,在四边形中, , , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 交于点若点是的中点,则的长为( ) A、 B、4 C、3 D、9. 如图,平面直角坐标系中,过原点的直线与双曲线交于、两点,在线段左侧作等腰三角形 , 底边轴,过点作轴交双曲线于点 , 连接 , 若 , 则的值是( )
A、 B、4 C、3 D、9. 如图,平面直角坐标系中,过原点的直线与双曲线交于、两点,在线段左侧作等腰三角形 , 底边轴,过点作轴交双曲线于点 , 连接 , 若 , 则的值是( )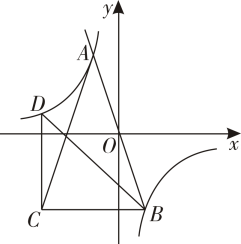 A、
A、
B、
C、
D、二、填空题(本大题共6小题,共30.0分)
-
10. 我县九年级考生约14978人,该人口数精确到千位大约为 .11. 分解因式: .12. 如图,《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕塑,刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间.掷铁饼者张开的双臂与肩宽可以近似看像一张拉满弦的弓,弧长约为米,“弓”所在的圆的半径约1.25米,则“弓”所对的圆心角度数为 .
 13. 从-2,1两个数中随机选取一个数记为m,再从-1,0,2三个数中随机选取一个数记为n,则m、n的取值使得一元二次方程x2-mx+n=0有两个不相等的实数根的概率是 .14. 如图,在中, , AB=10,BC=6, , 的平分线交于点 , 则 .
13. 从-2,1两个数中随机选取一个数记为m,再从-1,0,2三个数中随机选取一个数记为n,则m、n的取值使得一元二次方程x2-mx+n=0有两个不相等的实数根的概率是 .14. 如图,在中, , AB=10,BC=6, , 的平分线交于点 , 则 .
 15. 如图,和都是等腰直角三角形, , 点是边上的动点不与点、重合 , 与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为 , 则其中含所有正确结论的选项是 .
15. 如图,和都是等腰直角三角形, , 点是边上的动点不与点、重合 , 与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为 , 则其中含所有正确结论的选项是 .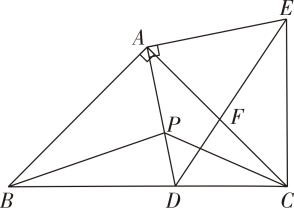
三、计算题
-
16. 计算 .
四、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 先化简,再求代数式的值,其中 .18. 如图,菱形中, , 分别为 , 上的点,且 , 连接并延长 , 与的延长线交于点 , 连接 .
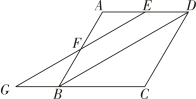 (1)、求证:四边形是平行四边形;(2)、连接 , 若 , , 求的长.19. 某初中举行硬笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如图两幅不完整的统计图.
(1)、求证:四边形是平行四边形;(2)、连接 , 若 , , 求的长.19. 某初中举行硬笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如图两幅不完整的统计图.
请结合图中相关信息解答下列问题:
(1)、扇形统计图中三等奖所在扇形的圆心角的度数是度;(2)、请将条形统计图补全;(3)、获得一等奖的同学中有来自七年级,有来自九年级,其他同学来自八年级.现准备从获得一等奖的同学中任选人参加市级硬笔书法大赛.请通过列表或画树状图的方法求所选出的人中既有七年级同学又有九年级同学的概率.20. 如图所示,某钓鱼爱好者周末到渭河边钓鱼,经测量某段河堤的坡角为 , 堤坡面长为米,钓竿的倾斜角即是 , 钓竿长为米,若与钓鱼线的夹角为 , 求浮漂与河提下端之间的距离.注:在本题中我们将钓竿和钓鱼线都分别看成段 21. 为迎接“国家创卫”检查,我市环卫局准备购买 , 两种型号的垃圾箱.通过市场调研发现:购买个型垃圾箱和个型垃圾箱需元;购买个型垃圾箱和个型垃圾箱共需元.(1)、求每个型垃圾箱和型垃圾箱各多少元?(2)、该市现需要购买 , 两种型号的垃圾箱个,其中购买型垃圾箱不超过个.求购买垃圾箱的总花费元与型垃圾箱个之间的函数关系式;(3)、在中,当购买型垃圾箱个数多少时总费用最小,最小费用是多少?
21. 为迎接“国家创卫”检查,我市环卫局准备购买 , 两种型号的垃圾箱.通过市场调研发现:购买个型垃圾箱和个型垃圾箱需元;购买个型垃圾箱和个型垃圾箱共需元.(1)、求每个型垃圾箱和型垃圾箱各多少元?(2)、该市现需要购买 , 两种型号的垃圾箱个,其中购买型垃圾箱不超过个.求购买垃圾箱的总花费元与型垃圾箱个之间的函数关系式;(3)、在中,当购买型垃圾箱个数多少时总费用最小,最小费用是多少?
-