新疆喀什地区2023年中考三模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共9小题,共45.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的平方根是( )A、 B、 C、 D、2. 如图放置的正六棱柱,其左视图是( )
 A、
A、
B、
C、
D、 3. 单项式的系数是( )A、 B、 C、 D、4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
3. 单项式的系数是( )A、 B、 C、 D、4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图, , , 若 , 则的度数是( )
5. 如图, , , 若 , 则的度数是( )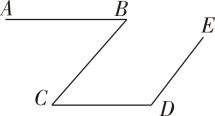 A、
A、
B、
C、
D、6. 若关于的一元二次方程有实数根,则的取值范围是( )A、 B、 C、 D、7. 在一个不透明的口袋里装有个小球,每个小球上都写有一个数字,分别是 , , , , 这些小球除数字不同外其它均相同,从中随机摸出两个小球,小球上的数字都是奇数的概率是( )A、 B、 C、 D、8. 为大力实施城市绿化行动,某小区规划设置一片面积为平方米的矩形绿地,并且长比宽多米,设绿地长为米,根据题意可列方程为( )A、 B、
C、 D、9. 如图,在正方形中,对角线、交于点 , 点是边上一个动点,于点 , 交于点 , 于点 , 交于点下列结论:∽;;;其中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共30.0分)
-
10. 分解因式 .11. 将抛物线先向左平移个单位长度,再向下平移个单位长度,得到的抛物线的解析式是 .12. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003,将0.0000003用科学记数法可以表示为 .13. 如图,在中,的垂直平分线交于点 , 交于点 , 连接若 , , , 则的周长为 .
 14. 如图,已知的周长是 , 是的内接正三角形,作于点 , 则 .
14. 如图,已知的周长是 , 是的内接正三角形,作于点 , 则 . 15. 如图,正方形的边轴,点、在轴上,已知点的坐标是 , 反比例函数的图象经过点 , 交于点 , 则点的坐标是 .
15. 如图,正方形的边轴,点、在轴上,已知点的坐标是 , 反比例函数的图象经过点 , 交于点 , 则点的坐标是 .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
-
16. 计算: .17. 解不等式组 , 并把解表示在数轴上.18. 如图,在矩形中,于点 , 于点 , 连接、 .
 (1)、求证:;(2)、判断四边形的形状,并说明理由.19. 月日是“世界地球日”,某校开展了环保知识网上答题竞赛活动,现从该校八、九年级各随机抽取名学生的成绩进行整理,描述和分析成绩用表示,单位:分 , 共分成四个组: , , , 给出了部分信息如下:
(1)、求证:;(2)、判断四边形的形状,并说明理由.19. 月日是“世界地球日”,某校开展了环保知识网上答题竞赛活动,现从该校八、九年级各随机抽取名学生的成绩进行整理,描述和分析成绩用表示,单位:分 , 共分成四个组: , , , 给出了部分信息如下:
八年级名学生的成绩: , , , , , , , , , .
九年级名学生的成绩在组的数据: , , , , .
八、九年级抽取学生成绩统计表年级
平均数
中位数
众数
八年级
九年级

根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、求八年级此次抽取的名学生的平均成绩;(3)、学校拟将成绩大于或等于分的学生评为“环保达人”予以表扬,若该校八、九年级各人参加了此次网上答题竞赛活动,估计八、九年级受表扬的学生总人数是多少?20. 数学实践活动中,为了测量公园内被花坛隔开的、两点的距离,同学们在外选择一点 , 从处测得点在南偏西方向,点在南偏东方向,的长度为米,求、两点的距离参考数据: , , , , , 21. 为扎实推进“五育”并举工作,加强劳动教育,学校花元购买一批型劳动工具,经过一段时间后,需购买第二批型劳动工具,此时每件涨价元,购买与第一批同等数量的型劳动工具花费了元.(1)、学校购买的第一批型劳动工具每件的价格为多少元?(2)、若学校需要购买第三批劳动工具共件,其中型劳动工具的单价和第二批相同,型劳动工具每件元,计划购买、两种劳动工具的总金额不超过元,则最多可以购买多少件型劳动工具?
21. 为扎实推进“五育”并举工作,加强劳动教育,学校花元购买一批型劳动工具,经过一段时间后,需购买第二批型劳动工具,此时每件涨价元,购买与第一批同等数量的型劳动工具花费了元.(1)、学校购买的第一批型劳动工具每件的价格为多少元?(2)、若学校需要购买第三批劳动工具共件,其中型劳动工具的单价和第二批相同,型劳动工具每件元,计划购买、两种劳动工具的总金额不超过元,则最多可以购买多少件型劳动工具?

