北京市石景山区2023年中考二模数学考试试卷
试卷更新日期:2023-09-27 类型:中考模拟
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 某几何体的三视图如图,则该几何体是( )
 A、圆柱
A、圆柱
B、圆锥
C、长方体
D、三棱柱2. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、3. 若一个多边形的内角和为 , 则该多边形的边数为( )A、 B、 C、 D、4. 如图,在中, , 分别是边 , 上的点, , 若的面积为 , 则的面积为( )
A、 B、 C、 D、3. 若一个多边形的内角和为 , 则该多边形的边数为( )A、 B、 C、 D、4. 如图,在中, , 分别是边 , 上的点, , 若的面积为 , 则的面积为( ) A、 B、 C、 D、5. 如图,为的直径, , 为上的点,若 , 则的度数为( )
A、 B、 C、 D、5. 如图,为的直径, , 为上的点,若 , 则的度数为( ) A、 B、 C、 D、6. 一组数据: , , , , , 若添加一个数据 , 则发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差7. 如图显示了某林业部门统计某种树苗在本地区相同条件下的移植成活试验的结果.
A、 B、 C、 D、6. 一组数据: , , , , , 若添加一个数据 , 则发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差7. 如图显示了某林业部门统计某种树苗在本地区相同条件下的移植成活试验的结果.
下面有四个推断:
当移植的棵树是时,成活的棵树是 , 所以“移植成活”的概率是;
随着移植棵树的增加,“移植成活”的频率总在附近摆动,显示出一定的稳定性,可以估计“移植成活”的概率是;
与试验相同条件下,若移植棵这种树苗,可能成活棵;
在用频率估计概率时,移植棵树时的频率一定比移植棵树时的频率更准确
其中合理的是( )A、 B、 C、 D、8. 如图,在中, , 点是边上一动点不与
点 , 重合 , 过点作交于点设 , 的长为 ,
的面积为 , 则与 , 与满足的函数关系分别为( ) A、一次函数关系,二次函数关系
A、一次函数关系,二次函数关系
B、反比例函数关系,二次函数关系
C、一次函数关系,反比例函数关系
D、反比例函数关系,一次函数关系二、填空题(本大题共8小题,共16.0分)
-
9. 若在实数范围内有意义,则实数的取值范围为 .10. 分式方程的解是 .11. 写出一个比大且比小的整数是.12. 如果 , 那么代数式的值为 .13. 在平面直角坐标系中,若点 , 在反比例函数y=(k>0)的图象上,则填“”,“=”或“” .14. 如图,在矩形中,点 , 分别为 , 的中点,若 , 则的长为 .
 15. 如图,在中, , 平分交于点若 , , 则的面积为 .
15. 如图,在中, , 平分交于点若 , , 则的面积为 .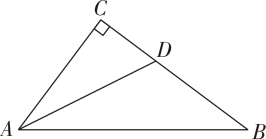 16. 有黑、白各张卡片,分别写有数字至把它们像扑克牌那样洗过后,数字朝下,如图排成两行,排列规则如下:
16. 有黑、白各张卡片,分别写有数字至把它们像扑克牌那样洗过后,数字朝下,如图排成两行,排列规则如下:
从左至右,按数字从小到大的顺序排列;
黑、白卡片数字相同时,黑卡片放在左边.
将第一行卡片用大写英文字母按顺序标注,第二行卡片用小写英文字母按顺序标注,则白卡片数字摆在了标注字母 的位置,标注字母的卡片写有数字 .
三、解答题(本大题共12小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 解不等式组:19. 已知:如图 , 直线及外一点 .

求作:直线 , 使得 .
作法:如图 ,
在直线上任取一点 , 连接;
为圆心,长为半径作弧,交直线于点;
分别以点 , 为圆心,长为半径作弧,两弧在直线外交于一点;
作直线 .
直线就是所求作的直线.(1)、使用直尺和圆规,依作法补全图形保留作图痕迹;(2)、完成下面的证明.
证明:连接 .
▲ ,
四边形是 ▲ 形( )(填推理的依据).
.20. 已知关于的一元二次方程
(1)、求证:该方程总有两个不相等的实数根;(2)、若 , 且该方程的一个根是另一个根的倍,求的值.21. 如图,菱形的对角线 , 相交于点 , 过点作 , 过点作交于点 . (1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.22. 在平面直角坐标系中,函数的图象过点 , .(1)、求该函数的解析式;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.23. 某社区通过公益讲座的方式普及垃圾分类知识为了了解居民对相关知识的了解情况及讲座效果,请居民在讲座前和讲座后分别回答了一份垃圾分类知识问卷,从中随机抽取名居民的两次问卷成绩百分制 , 并对数据成绩进行整理、描述和分析下面给出了部分信息.
(1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.22. 在平面直角坐标系中,函数的图象过点 , .(1)、求该函数的解析式;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.23. 某社区通过公益讲座的方式普及垃圾分类知识为了了解居民对相关知识的了解情况及讲座效果,请居民在讲座前和讲座后分别回答了一份垃圾分类知识问卷,从中随机抽取名居民的两次问卷成绩百分制 , 并对数据成绩进行整理、描述和分析下面给出了部分信息.
这名居民讲座前、讲座后成绩得分统计图如图:

这名居民讲座前、讲座后成绩的平均数、中位数、方差如下:平均数
中位数
方差
讲座前
讲座后
结合讲座后成绩 , 被抽取的名居民中有人获得“参与奖” , 有人获得“优秀奖” , 有人获得“环保达人奖” , 其中成绩在这一组的是:
根据以上信息,回答下列问题:(1)、居民小张讲座前的成绩为分,讲座后的成绩为分,在图中用“”圈出代表居民小张的点;(2)、写出表中的值;(3)、参加公益讲座的居民有人,估计能获得“环保达人奖”的有 人24. 年月日,世界泳联跳水世界杯首站比赛在西安圆满落幕,中国队共收获金银,位列奖牌榜第一赛场上运动员优美的翻腾、漂亮的入水令人赞叹不已在米跳台跳水训练时,运动员起跳后在空中的运动路线可以看作是抛物线的一部分建立如图所示的平面直角坐标系,从起跳到入水的过程中,运动员的竖直高度单位:与水平距离单位:近似满足函数关系 .
某跳水运动员进行了两次训练.
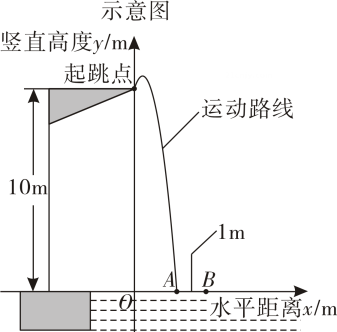 (1)、第一次训练时,该运动员的水平距离与竖直高度的几组数据如下:
(1)、第一次训练时,该运动员的水平距离与竖直高度的几组数据如下:水平距离
竖直高度
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系;
运动员必须在距水面前完成规定的翻腾动作并调整好入水姿势,否则就会出现失误在这次训练中,测得运动员在空中调整好入水姿势时,水平距离为 , 判断此次跳水会不会出现失误,并说明理由;(2)、第二次训练时,该运动员的竖直高度与水平距离近似满足函数关系如图,记该运动员第一次训练的入水点为 , 若运动员在区域内含 , 入水能达到压水花的要求,则第二次训练 达到要求填“能”或“不能” .25. 如图,AB是的直径,弦于点 , 过点作交的延长线于点 , 点是延长线上一点, .
 (1)、求证:是的切线;(2)、若 , 求半径的长.26. 在平面直角坐标系中,抛物线与轴交于点 , 将点向右平移个单位长度,得到点 .(1)、若 , 点在抛物线上,求抛物线的解析式及对称轴;(2)、若抛物线与线段恰有一个公共点,结合函数图象,求的取值范围.27. 如图,在中, , , 平分交于点 , 点是上一点且 ,
(1)、求证:是的切线;(2)、若 , 求半径的长.26. 在平面直角坐标系中,抛物线与轴交于点 , 将点向右平移个单位长度,得到点 .(1)、若 , 点在抛物线上,求抛物线的解析式及对称轴;(2)、若抛物线与线段恰有一个公共点,结合函数图象,求的取值范围.27. 如图,在中, , , 平分交于点 , 点是上一点且 ,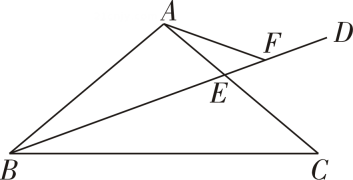 (1)、求的大小用含的式子表示;(2)、连接用等式表示线段与的数量关系,并证明.28. 在平面直角坐标系中,对于点不与点重合和线段 , 给出如下定义:连接 , 平移线段 , 使点与线段的中点重合,得到线段”,则称点为线段的“中移点”已知的半径为 .
(1)、求的大小用含的式子表示;(2)、连接用等式表示线段与的数量关系,并证明.28. 在平面直角坐标系中,对于点不与点重合和线段 , 给出如下定义:连接 , 平移线段 , 使点与线段的中点重合,得到线段”,则称点为线段的“中移点”已知的半径为 . (1)、如图,点 , 点 ,
(1)、如图,点 , 点 ,
点为与轴正半轴的交点, , 求的值;
点为上一点,若在直线上存在线段的“中移点” , 求的取值范围.(2)、点是上一点,点在线段上,且若是外一点,点为线段的“中移点”,连接 , 当点在上运动时,直接写出长的最大值与最小值的差用含的式子表示 .