广东省东莞市凤岗镇2023年中考一模数学试卷
试卷更新日期:2023-09-26 类型:中考模拟
一、选择题(共10小题,满分30分,每小题3分)
-
1. 有理数-22的相反数是( )A、22 B、-22 C、 D、-2. 2021年是中国共产党建党百年,走过百年光辉历程的中国共产党,成为拥有9100多万名党员的世界最大的马克思主义执政党.将“9100万”用科学记数法表示应为( )A、 9.1×103 B、0.91×104 C、9.1×107 D、91×1063. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
 A、
A、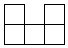 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、a2•a3=a6 B、a2+a2=a4 C、(a3)2=a6 D、a6÷a2=a35. 如图,直线 , 直线 , 若 , 则( )
4. 下列计算正确的是( )A、a2•a3=a6 B、a2+a2=a4 C、(a3)2=a6 D、a6÷a2=a35. 如图,直线 , 直线 , 若 , 则( ) A、 B、 C、 D、6. 小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
A、 B、 C、 D、6. 小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:步数(万步)
1.0
1.1
1.2
1.3
1.4
天数
3
3
9
11
4
在每天所走的步数这组数据中,众数和中位数分别是( )
A、1.3,1.25 B、1.3,1.3 C、1.4,1.3 D、1.3,1.17. 关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )A、k>-1 B、k<1 C、k>-1且k≠0 D、k<1且k≠08. 如图,已知AB是⊙O的直径,CD是弦,若∠BCD=24°,则∠ABD=( )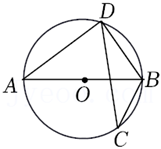 A、54° B、56° C、64° D、66°9. 如图,等边△ABC的边长为4,D,E,F分别为边AB,BC,AC的中点,分别以A,B,C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是( )
A、54° B、56° C、64° D、66°9. 如图,等边△ABC的边长为4,D,E,F分别为边AB,BC,AC的中点,分别以A,B,C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是( ) A、π B、2π C、4π D、6π10. 如图,已知点A、B在反比例函数y=(k>0,x>0)的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M , 设点P的运动时间为t , △POM的面积为S , 则S关于t的函数图象大致为( )
A、π B、2π C、4π D、6π10. 如图,已知点A、B在反比例函数y=(k>0,x>0)的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M , 设点P的运动时间为t , △POM的面积为S , 则S关于t的函数图象大致为( ) A、
A、 B、
B、 C、
C、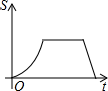 D、
D、
二、填空题(共5小题,满分15分,每小题3分)
-
11. 单项式-x2y的系数是 .12. 因式分解:ax2﹣4ay2=.13. 不等式组的整数解有个.14. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为30°,测得点处的俯角为45°.又经过人工测量操控者和教学楼之间的水平距离为80米,教学楼的高度米.(注:点、、、都在同一平面上,参考数据: , 结果保留整数).
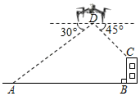 15. 如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF , 若∠BFC=30°,则EF长的最大值为 .
15. 如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF , 若∠BFC=30°,则EF长的最大值为 .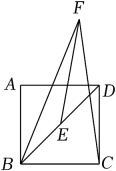
三、解答题(共8小题,满分75分)
-
16. 计算:(1-π)0-2cos30°+|-|-()-1 .17. 先化简,再求值(1+)÷ , 其中x=-1.18. 如图,已知平行四边形ABCD(AD>AB),连接对角线AC .
 (1)、请用直尺和圆规作AC的垂直平分线,分别交AD于点E , 交BC于点F , 交AC于点O , 并连接CE和AF;(保留作图痕迹)(2)、若AE=5,求四边形AECF的周长.19. 在全校汉字听写大赛中,选择了50名学生参加区级决赛.根据测试成绩绘制出部分频数分布表和部分频数分布直方图,结合图表完成下列问题:
(1)、请用直尺和圆规作AC的垂直平分线,分别交AD于点E , 交BC于点F , 交AC于点O , 并连接CE和AF;(保留作图痕迹)(2)、若AE=5,求四边形AECF的周长.19. 在全校汉字听写大赛中,选择了50名学生参加区级决赛.根据测试成绩绘制出部分频数分布表和部分频数分布直方图,结合图表完成下列问题: (1)、求表中a的值;
(1)、求表中a的值;组别
成绩x分
频数(人)
第1组
25≤x<30
4
第2组
30≤x<35
8
第3组
35≤x<40
16
第4组
40≤x<45
a
第5组
45≤x<50
10
(2)、补全频数分布直方图;(3)、规定测试成绩不低于40分为优秀,则本次测试的优秀率是多少?(4)、第5组10名同学中,有4名男同学(他们分别是A、B、C、D),现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求A与B能分在同一组的概率.20. 如图,▱ABCD放置在平面直角坐标系中,已知点A(-2,0),B(-6,0),D(0,3),点C在反比例函数y=的图象上. (1)、直接写出点C坐标,并求反比例函数的表达式;(2)、将▱ABCD向上平移得到▱EFGH , 使点F在反比例函数y=的图象上,GH与反比例函数图象交于点M . 连结AE , 求AE的长及点M的坐标.21. 为打造校园劳动实践基地,某学校计划在3月份购进甲、乙两种植株进行培育.已知甲植株的单价是乙植株单价的 , 用900元购买的甲植株数量比用600元购买的乙植株数量多10株.(1)、求甲、乙植株的单价分别是多少元.(2)、该学校决定购买甲、乙两种植株共150株,其中乙植株的数量不超过甲植株数量的 , 如何购进两种植株才能使费用最低,最低费用是多少?22. 如图,PA为⊙O的切线,A为切点,过A作AB⊥OP , 垂足为C , 交⊙O于点B , 延长BO与PA的延长线交于点D .
(1)、直接写出点C坐标,并求反比例函数的表达式;(2)、将▱ABCD向上平移得到▱EFGH , 使点F在反比例函数y=的图象上,GH与反比例函数图象交于点M . 连结AE , 求AE的长及点M的坐标.21. 为打造校园劳动实践基地,某学校计划在3月份购进甲、乙两种植株进行培育.已知甲植株的单价是乙植株单价的 , 用900元购买的甲植株数量比用600元购买的乙植株数量多10株.(1)、求甲、乙植株的单价分别是多少元.(2)、该学校决定购买甲、乙两种植株共150株,其中乙植株的数量不超过甲植株数量的 , 如何购进两种植株才能使费用最低,最低费用是多少?22. 如图,PA为⊙O的切线,A为切点,过A作AB⊥OP , 垂足为C , 交⊙O于点B , 延长BO与PA的延长线交于点D . (1)、求证:PB为⊙O的切线;(2)、若OB=3,OD=5,求AB的长.23. 某“数学学习兴趣小组”成员在复习《图形的变化》时,对下面的图形背景产生了浓厚的兴趣,并尝试运用由“特殊到一般”的思想进行了探究:
(1)、求证:PB为⊙O的切线;(2)、若OB=3,OD=5,求AB的长.23. 某“数学学习兴趣小组”成员在复习《图形的变化》时,对下面的图形背景产生了浓厚的兴趣,并尝试运用由“特殊到一般”的思想进行了探究:
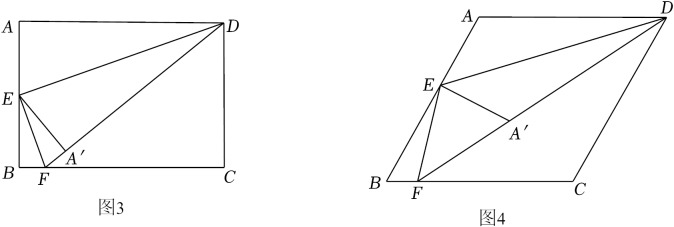 (1)、【问题背景】如图1,正方形ABCD中,点E为AB边上一点,连接DE , 过点E作EF⊥DE交BC边于点F , 将△ADE沿直线DE折叠后,点A落在点A'处,当∠BEF=25°,则∠FEA'=°.(2)、【特例探究】如图2,连接DF , 当点A'恰好落在DF上时,求证:AE=2A'F .(3)、【深入探究】如图3,若把正方形ABCD改成矩形ABCD , 且AD=mAB , 其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.(4)、【拓展探究】如图4,若把正方形ABCD改成菱形ABCD , 且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.
(1)、【问题背景】如图1,正方形ABCD中,点E为AB边上一点,连接DE , 过点E作EF⊥DE交BC边于点F , 将△ADE沿直线DE折叠后,点A落在点A'处,当∠BEF=25°,则∠FEA'=°.(2)、【特例探究】如图2,连接DF , 当点A'恰好落在DF上时,求证:AE=2A'F .(3)、【深入探究】如图3,若把正方形ABCD改成矩形ABCD , 且AD=mAB , 其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.(4)、【拓展探究】如图4,若把正方形ABCD改成菱形ABCD , 且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.