广东省深圳市大鹏新区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-26 类型:期末考试
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列四个图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. “翻开人教版数学九年级下册,恰好翻到第页”,这个事件是( )A、确定事件 B、不可能事件 C、必然事件 D、随机事件3. 小明在爬一小山时,第一阶段的平均速度为 , 所用时间为t;第二阶段的平均速度为v,所用时间为 , 则小明在爬这一小山的平均速度为( )A、 B、 C、 D、4. 用三角板作的高,下列作法正确的是( )A、
2. “翻开人教版数学九年级下册,恰好翻到第页”,这个事件是( )A、确定事件 B、不可能事件 C、必然事件 D、随机事件3. 小明在爬一小山时,第一阶段的平均速度为 , 所用时间为t;第二阶段的平均速度为v,所用时间为 , 则小明在爬这一小山的平均速度为( )A、 B、 C、 D、4. 用三角板作的高,下列作法正确的是( )A、 B、
B、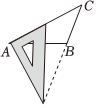 C、
C、 D、
D、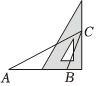 5. 下列计算中,正确的是( )A、 B、 C、 D、6. 春暖花开,美丽云南景色宜人.一位“驴友”早晨8:00从家出发到郊外赏花.他所走的路程(千米)随时间(时)变化的情况如图所示.则下面说法中错误的是( )
5. 下列计算中,正确的是( )A、 B、 C、 D、6. 春暖花开,美丽云南景色宜人.一位“驴友”早晨8:00从家出发到郊外赏花.他所走的路程(千米)随时间(时)变化的情况如图所示.则下面说法中错误的是( ) A、在这个变化过程中,自变量是时间,因变量是路程 B、他在途中休息了1小时 C、到9:00时他走的路程是4千米 D、他到达目的地所花的时间是4小时7. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( )
A、在这个变化过程中,自变量是时间,因变量是路程 B、他在途中休息了1小时 C、到9:00时他走的路程是4千米 D、他到达目的地所花的时间是4小时7. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( )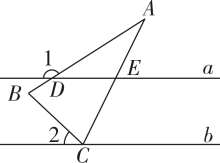 A、 B、 C、 D、8. 如图,点在的延长线上,下列条件能判断的是( )
A、 B、 C、 D、8. 如图,点在的延长线上,下列条件能判断的是( ) A、 B、 C、 D、9. 如图,小明在以为顶角的等腰三角形中用圆规和直尺作图,作出过点的射线交于点然后又作出一条直线与交于点 , 连接 , 若的面积为 , 则的面积为( )
A、 B、 C、 D、9. 如图,小明在以为顶角的等腰三角形中用圆规和直尺作图,作出过点的射线交于点然后又作出一条直线与交于点 , 连接 , 若的面积为 , 则的面积为( ) A、 B、 C、 D、10. 如图,已知正方形与正方形的边长分别为、 , 如果 , , 则阴影部分的面积为( )
A、 B、 C、 D、10. 如图,已知正方形与正方形的边长分别为、 , 如果 , , 则阴影部分的面积为( ) A、38 B、39 C、40 D、41
A、38 B、39 C、40 D、41二、填空题(本大题共5小题,共15分)
-
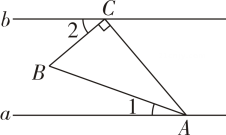
11. 已知直线 , 将一块含角的直角三角板按如图方式放置,若 , 则的度数为 .
 12. 如图,已知 , , , 在同一条直线上, , , , 若 , , 则 .
12. 如图,已知 , , , 在同一条直线上, , , , 若 , , 则 .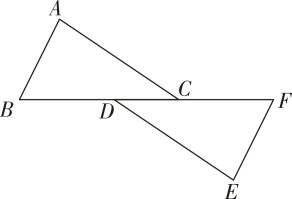 13. 如图,点、、、分别在锐角的边上,四边形为矩形, , , , 则 .
13. 如图,点、、、分别在锐角的边上,四边形为矩形, , , , 则 .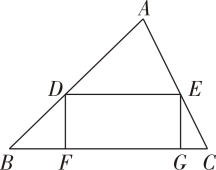 14. 南京梅花山被誉为“天下第一梅山”,每年月左右,万株梅花竞相开放,层层叠叠,云蒸霞蔚,繁花满山,一片香海一支梅花的直径约为 , 这个数用科学记数法表示为15. 如图,中,点是的垂直平分线与的交点,交延长于点 , 若 , , , 则的面积为 .
14. 南京梅花山被誉为“天下第一梅山”,每年月左右,万株梅花竞相开放,层层叠叠,云蒸霞蔚,繁花满山,一片香海一支梅花的直径约为 , 这个数用科学记数法表示为15. 如图,中,点是的垂直平分线与的交点,交延长于点 , 若 , , , 则的面积为 .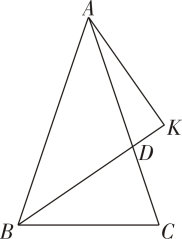
三、解答题(本大题共7小题,共55.0分。解答应写出文字说明,证明过程或演算步骤)
-
16. 计算:(1)、;(2)、 .17. 先化简,再求值 , 其中18. 一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.(1)、求摸到的球是白球的概率;(2)、小明又向这个口袋中放入了6个同样规格的球,若放入前后摸到白球的概率不变,则新放入的6个小球中有多少个白球?19. 深圳市从2016年到2022年的常住人口统计数据如下:
时间x/年
2016
2017
2018
2019
2020
2021
2022
常住人口y/千万人
请你根据表格回答下列问题:
(1)、表格中反映了和两个变量之间的关系,其中是自变量,是因变量;(2)、2020年,深圳的常住人口是千万人;(3)、哪段时间的常住人口增长较快?(4)、随着x的变化,y的变化趋势是什么?20. 如图 , 从边长为的正方形中剪掉一个边长为的正方形,然后将剩余部分拼成一个如图所示的长方形. (1)、上述操作能验证的等式是;填序号
(1)、上述操作能验证的等式是;填序号;; .
(2)、根据(1)中的等式,完成下列各题:已知 , , 求的值;
计算: .

